ЧАСТНЫЙ ИНСТИТУТ УПРАВЛЕНИЯ И ПРЕДПРИНИМАТЕЛЬСТВА

М. И. ОВСЕЕЦ

Е. М. СВЕТЛАЯ

СБОРНИК ЗАДАЧ

ПО ВЫСШЕЙ МАТЕМАТИКЕ

Линейная алгебра

Аналитическая геометрия

М

инск 2006

УДК 51

ББК 22,11я73

О 34

Рекомендовано к изданию редакционно-издательским советом

Частного института управления и предпринимательства

Авторы:

М. И. Овсеец, кандидат физико-математических наук,

доцент кафедры высшей математики и статистики

Частного института управления и предпринимательства;

Е. М. Светлая, преподаватель кафедры высшей математики и статистики

Частного института управления и предпринимательства

Рецензенты:

А. К. Вершина, профессор кафедры

материаловедения и технологии металлов Белорусского государственного технологического университета, доктор технических наук;

А. А. Егоров, доцент кафедры высшей математики

и математической физики Белорусского государственного университета, кандидат физико-математических наук

Рассмотрено и одобрено

на заседании кафедры высшей математики и статистики,

протокол № 6 от 23 января 2006 г.

Овсеец, М. И.

О 34 Сборник задач по высшей математике. Линейная алгебра. Аналитическая геометрия: учеб.-метод. пособие / М. И. Овсеец, Е. М. Светлая.– Минск: Частн. ин-т упр. и предпр., 2006.– 68 с.

Сборник задач содержит краткий теоретический материал, примеры и задачи по разделу «Линейная алгебра. Аналитическая геометрия».

Предназначен для студентов экономических специальностей, изучающих высшую математику Частного института управления и предпринимательства.

УДК 51

ББК 22.11я73

© Частный институт управления и предпринимательства, 2006

Г лава I. Линейная алгебра

1. Матрицы и действия над ними

Матрицей размера называется прямоугольная таблица чисел, содержащая т строк и п столбцов.

Матрица, у которой число строк равно числу столбцов , называется квадратной матрицей порядка п. Нулевой называется матрица, все элементы которой равны нулю. Ее обозначают буквой О.

Диагональной называется квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной и обозначается буквой Е.

Для матриц одинакового размера вводятся операции сложения и вычитания.

Для того чтобы сложить две матрицы и , достаточно сложить их соответствующие элементы. Операция обозначается .

Для того чтобы из матрицы вычесть матрицу , достаточно из каждого элемента матрицы А вычесть соответствующие элементы матрицы В. Операция обозначается .

Для того чтобы матрицу умножить на число , достаточно все элементы матрицы умножить на число . Операция обозначается или .

Произведение матрицы на матрицу вводится только для согласованных матриц, т. е. число столбцов матрицы должно равняться числу строк матрицы (число п). Операция обозначается .

Произведением матриц и называется такая матрица , каждый элемент которой равен сумме произведений элементов i-й строки матрицы на соответствующие элементы j-го столбца матрицы .

Произведение матриц не обладает свойством коммутативности, т. е. не всегда , даже если произведения имеют смысл.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Ее обозначают .

Примеры

1. Найти линейную комбинацию матриц

где , .

Р е ш е н и е.

+.

2. Найти произведения 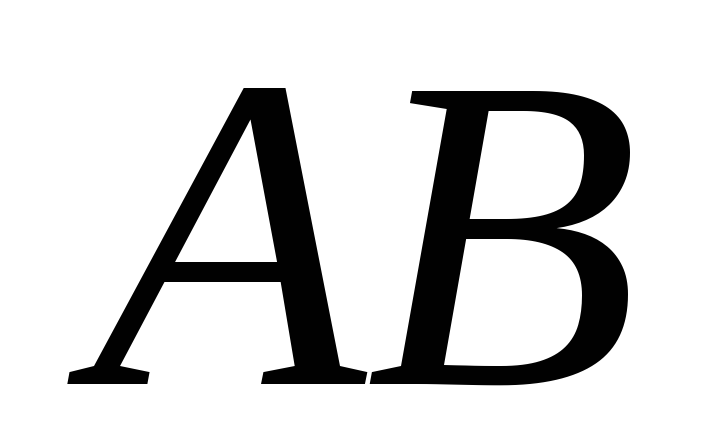, матриц:

.

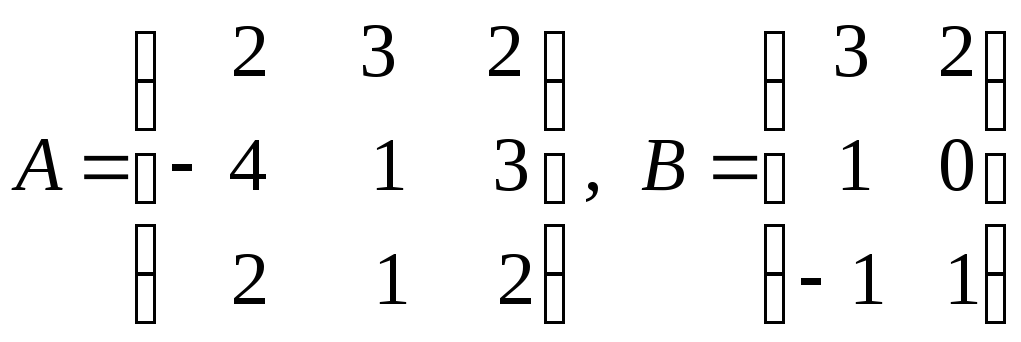Р е ш е н и е. Матрица А имеет размерность , матрица . Они являются согласованными. Матрица будет иметь размерность .

=

==.

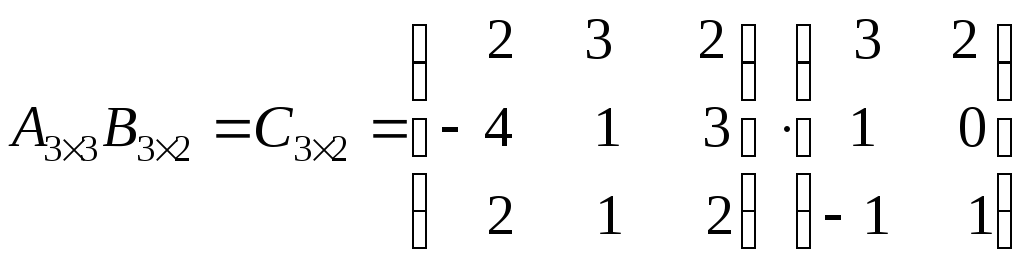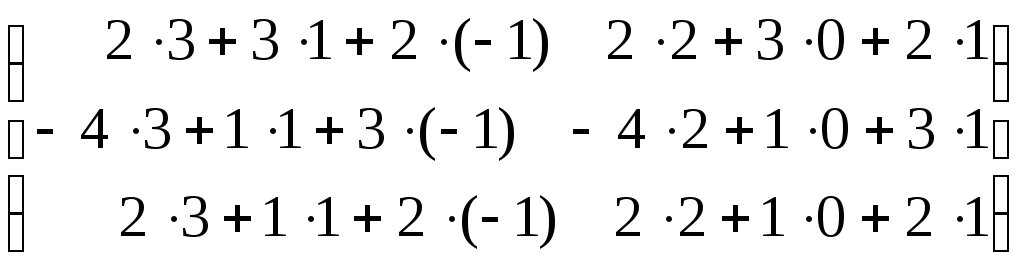Произведение не существует, так как число столбцов матрицы В не равно числу строк матрицы

3. Транспонировать матрицу .

Р е ш е н и е. Так как у матрицы А две строки и три столбца, то у матрицы будет три строки и два столбца:

.

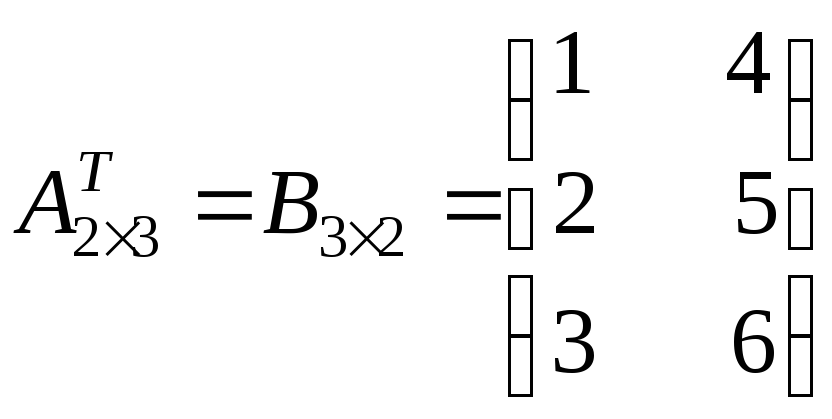4. Решить матричное уравнение 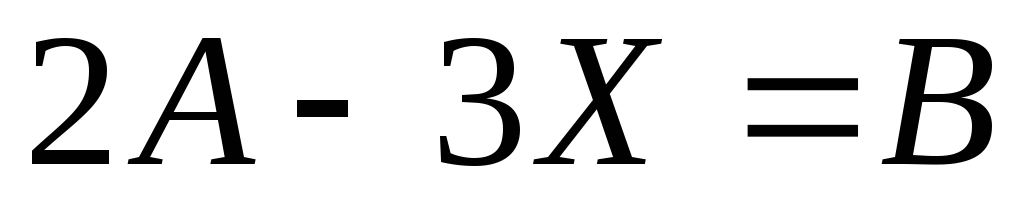, если Х – неизвестная матрица.

Р е ш е н и е. Используя свойства линейных операций над матрицами, найдем Х в общем виде:

Тогда

=

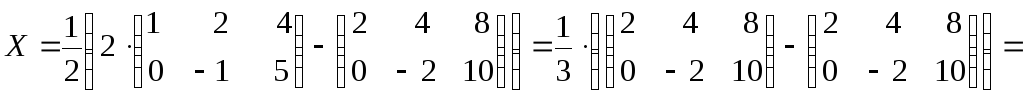
5. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М₁, М₂, и М₃, причем доставка единицы продукции с каждого молокозавода в магазин М₁ стоит 50 ден. ед., в магазин М₂ – 70, а в М₃ – 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.

Молокозавод	Магазин
1 2	М1 М2 М3
	20 35 10 15 27 8

Р е ш е н и е. Обозначим через А матрицу, данную нам в условии, а через В – матрицу, характеризующую стоимость доставки единицы продукции в магазины, т. е.

.

Тогда матрица затрат на перевозки будет иметь вид:

.

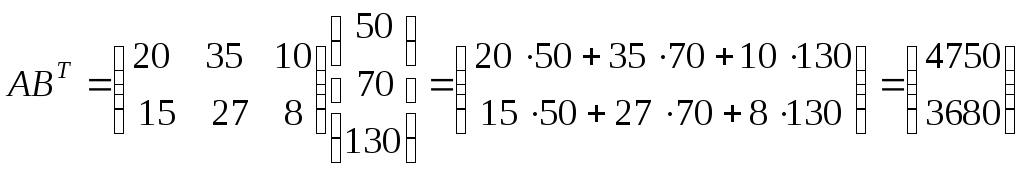Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй – 3680 ден. ед.

6. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей 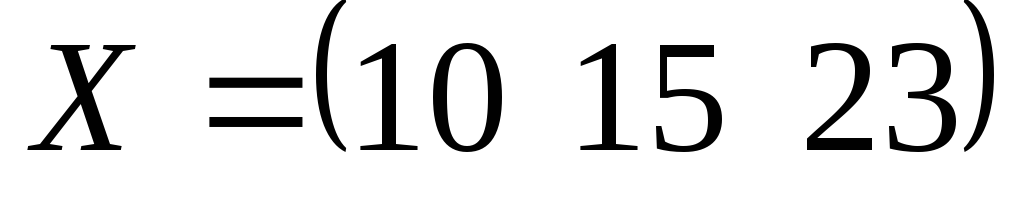. Используются ткани четырех типов 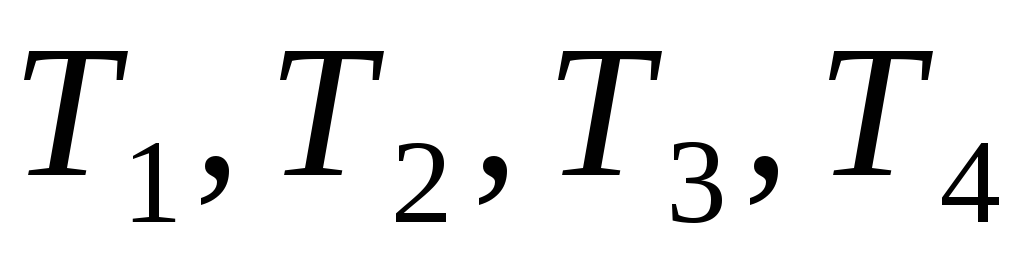. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица задает стоимость метра ткани каждого типа, а матрица – стоимость перевозки метра ткани каждого вида.

Изделие	Расход ткани
	Т1	Т2	Т3	Т4
Зимнее пальто Демисезонное пальто Плащ	5 3 0	1 2 0	0 0 4	3 2 3

1. Сколько метров ткани каждого типа потребуется для выполнения плана?

2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.

3. Определить стоимость всей ткани, необходимой для выполнения плана.

4. Подсчитать стоимость всей ткани с учетом ее транспортировки.

Р е ш е н и е. Обозначим через А матрицу, данную нам в условии, т. е.

.

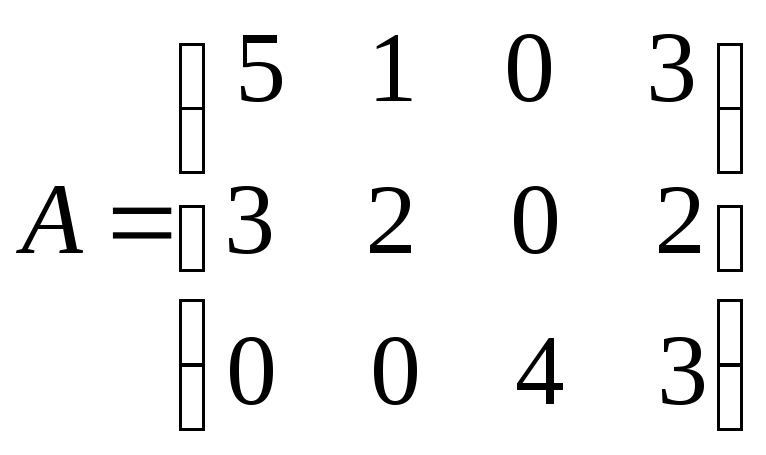Тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно матрицу Х умножить на матрицу А:

=.

Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицы А и С^Т:

.

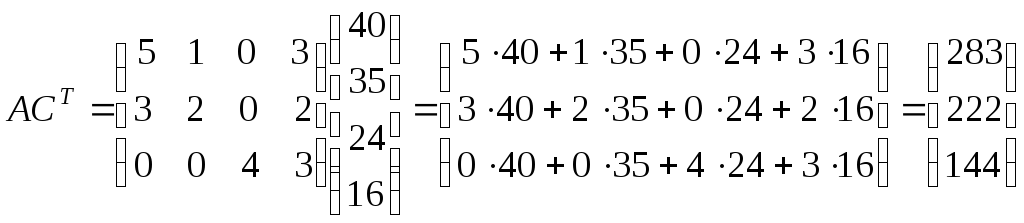Стоимость всей ткани, необходимой для выполнения плана, определится по формуле

.

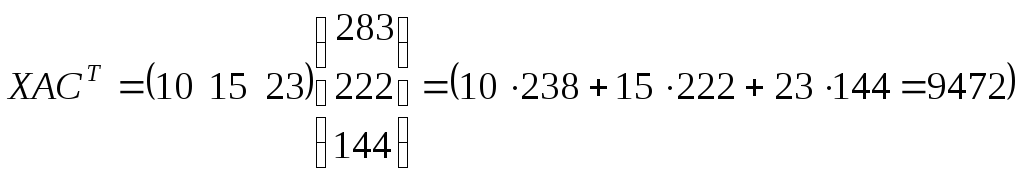Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина

.

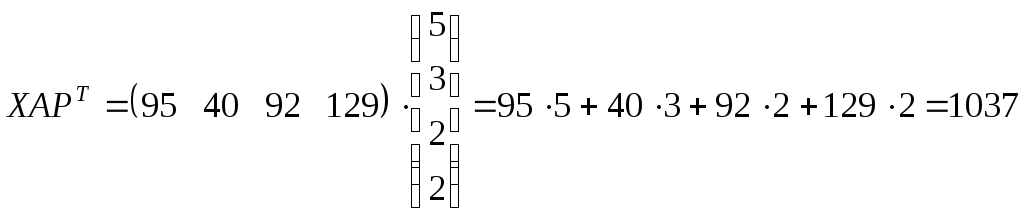Итак,