1.9. Аксонометрические проекции.

Сущность метода и основные понятия. Для наглядного изображе­ния расположенных в пространстве деталей относительно выбранных плос­костей проекций использовались проекции, называемые аксонометрическими (от древнегреческого «аксон» — ось, «метрио» — измеряю), т. е. означает измерение по осям. Их часто используют для наглядного изображения конструкций приборов, машин на чер­теже, особенно на начальных этапах конструирования.

Применяемые в отечественной конструкторской докумен­тации аксонометрические проекции стандартизованы в ГОСТ 2.317- 69.

Способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым, она отнесена в пространстве, проецируется параллель­но на некоторую плоскость, принятую за плоскость аксономет­рических проекций (эту плоскость называют также картинной плоскостью).

При их построении основные плоскости объекта располагают параллельно или перпендикулярно плоскостям проекций, при этом на каждой плоскости проекций два измерения предмета изоб­ражаются в натуральную величину, а третье отсутствует. Это положение соответствует требованиям, которые предъявляются к черте­жу быть обратимым простым в выполнении. Но наглядность таких изображений не всегда бывает достаточной. Если комплексный чертеж не создает достаточно полного представления о предмете, то в дополнение к нему выполняется более наглядное изображение ак­сонометрия предмета. Аксонометрия может быть как центральной, так и параллельной проекцией предмета, мы будем рас­сматривать аксонометрию как параллельную проекцию.

Сущность метода аксонометрического проецирования состоит в следующем, предмет в пространстве относят к прямоугольной сис­теме координатных осей (декартовой системе координат), а затем вместе с осями проецируют на некоторую плоскость , плоскость аксонометрической проекции. Направление проецирования при этом выбирают непараллельное координатным осям. (

Рис. 1.102

Рис. 1.102)

Полученный в плоскости  чертеж называется аксонометрическим. Получен­ная проекция отражает три измерения предмета и является обрати­мым чертежом. Определим, как в аксонометрии достигается обратимость изображения. Представим себе в пространстве точку А, отнесем ее к си­стеме прямоугольных (декартовых) координат. (Рис. 1.103) Отрезки ОА_х, А_хА₁, A₁A соответственно равны расстояниям от точки до координатных плоскостей: ОА_х - координате х, А_хА₁ – координате у, A₁A - координате z. Пусть единицей измерения для всех координатных осей будет отрезок е — натуральный масштаб. Отложим эти отрезки на каждой из осей (e_х, е_y, е_г). Для каждой точки пространства можно построить координатную ломаную AA₁А_хО (пространственная лома­ная), измерив отрезки которой с помощью натурального масштаба определим координаты точки.

В

Рис. 1.103

ыберем направление проецирования s и спроецируем точку А вместе с координатными осями и координатной ломаной на плос­кость  (см. рис. 1.103). Проекцию точки на эту плоскость А₀ называют аксонометрической проекцией. Проекцию координатной ломаной А₀А₁0А_х0О₀ называют аксонометрической координатной ломаной (плоская ломаная). Проекции координатных осей O₀C₀, O₀Y₀, O₀Z₀ называют аксонометрическими осями. Проекции е_х0, е_y0, е_z0 нату­ральных масштабов называют аксонометрическими масштабами. В общем случае они не равны натуральному масштабу и не равны между собой, их принимают за единицы длины по соответствую­щим аксонометрическим осям. Поскольку при параллельном проецировании соотношение длин отрезков, принадлежащих объекту, сохраняется и на их проекциях, то аксонометрические координаты численно равны натуральным.

Измерив отрезки аксонометрической координатной ломаной А₀А₁0А_х0О₀ с помощью соответствующих аксонометрических масш­табов е_х0, е_y0, е_z0 получим численное значение координат точки А. Благодаря этому в пространственной системе координат, однознач­но определим положение точки. Следовательно, изображение объекта можно считать обратимым.

Искажения отрезков осей координат при их проецировании на плоскость  характеризуется так называемыми коэффициентами искажения. Это отношение аксонометрического масштаба к нату­ральному. Обозначим через k, m, n показатели искажений по осям OX, OY, OZ. Тогде:

k= e_x/e_x0; m = e_y/e_y0; n = e_z/e_z0,

В зависимости от соотношения коэффициентов искажения аксо­нометрические проекции могут быть:

- изометрическими, когда коэффициенты искажения по всем трем осям равны между собой k = т = п;

- диметрическими, когда коэффициенты искажения по двум лю­бым осям равны между собой, а по третьей - отличаются от первых двух k = m  n;

- триметрическими, когда все три коэффициента искажения по осям различны, т.е. k  m n и k  n.

Аксонометрические проекции различаются также по тому углу φ, который образуется проецирующим лучом с аксонометрической плоскостью проекций  (см. рис. 1.103). Если φ 90°, то аксонометри­ческая проекция называется косоугольной, а если φ = 90° - прямоу­гольной.

Естественно, что изометрические, диметрические и триметрические проекции могут быть как прямоугольными, так и косоугольными.

Очевидно, что принимая различное взаимное расположение де­картовой системы координат и плоскости аксонометрических про­екций и задавая разные направления проецирования, можно полу­чить множество аксонометрических проекций, отличающихся друг от друга как направлением аксонометрических осей, так и величиной коэффициентов искажения вдоль этих осей.

Справедливость этого утверждения была доказана немецким гео­метром Карлом Польке. Теорема Польке утверждает, что три от­резка произвольной длины, лежащие в одной плоскости и выходя­щие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных осях координат от начала.

В аксонометрии общего вида коэффициенты искажения и угол φ находятся в опреде­ленной зависимости, которая выражается формулой, называемой основной формулой аксонометрии:

k²+m²+n² = 2+ctg² φ. (8.1)

Аксонометрические проекции. На практике используют аксонометрические проекции, кото­рые кроме наглядности изображения обеспечивают простоту построения. К ним относятся прямоугольные аксонометрические проекции изометрия и диметрия, а также косоугольные аксономет­рические проекции фронтальная диметрия и горизонтальная изометрия. (Рис. 1.104)

Прямоугольная изометрическая проекция. В прямоугольной изометрической проекции коэффициенты ис­кажения по всем трем осям одинаковы k = т = п. Используя форму­ле (8.1), и считая, что ctg² φ = 0, получим 3k² = 2,тогда k = √2/3 = 0,82.

Следовательно, при построении изометрической проекции раз­меры предмета, откладываемые по аксонометрическим осям, умно­жаются на 0,82. Такой пересчет неудобен. Поэтому изометрическую проекцию для упрощения выполняют без уменьшения размеров (ис­кажения) по осям, т. е. коэффициент искажения принимают равным 1. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры, чем в действительнос­ти. Увеличение в этом случае составляет 22 % и выражается числом 1,22. Каждый отрезок, направленный по осям OX, OY, OZ, или па­раллельно им, сохраняет свою величину. Расположение осей, а так­же изображение детали в прямоугольной изометрической проекции показано на рис. 1.104,а.

Прямоугольная диметрическая проекция. Коэффициенты искажения в прямоугольной диметрической про­екции выбирают следующими k = п; т = 1/2 k. Тогда, используя основную формулу аксонометрии, п

Рис. 1.104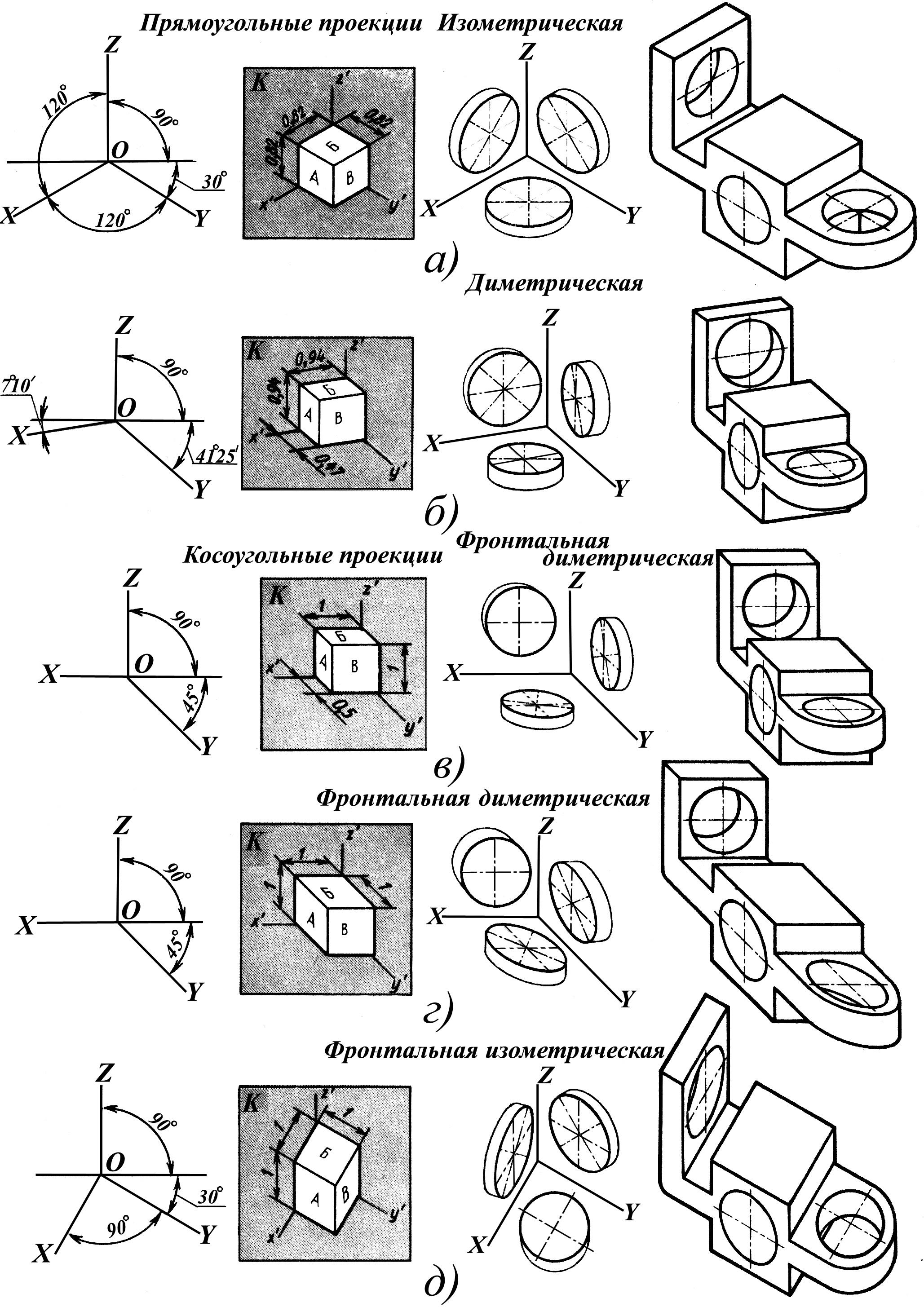

олучим:

2k² + 1/4k² = 2; k = √8/9 ≈ 0,94; m ≈ 0,47

В целях упрощения построений, как и в изометрических проек­циях, коэффициент искажения по осям ОХ и OZ принимают равным 1, по оси OY коэффициент искажения равен 0,5. По осям ОХ и OZ, или параллельно им все размеры откладываются в натуральную ве­личину, по оси OY— размеры уменьшают вдвое.

Увеличение в этом случае составляет 6% и выражается числом 1,06. Расположение осей в прямоугольной диметрической проекции и изображение детали показано на рис.1.104, б. С достаточ­ной для практических целей точностью оси ОХ и OY строят по тан­генсам углов tg 7°10'=1/8; tg 41°25'=7/8.

Продолжение оси OY за центр О является биссектрисой угла XOZ, что также может быть использовано для построения оси OY.

Косоугольные аксонометрические проекции. Косоугольные аксонометрические проекции чаще всего использу­ют на плоскостях, параллельных плоскостям проекций, т.е. в тех слу­чаях, когда необходимо сохранить неискаженными фигуры, располо­женные в плоскостях, параллельных выбранной плоскости проекций.

В случае, когда фигуры располагаются параллельно фронталь­ной плоскости проекций, рационально применять фронтальную диметрию.

Во фронтальной диметрии коэффициенты искажения по оси ОХ и OZ принимают равными 1, а по оси OY - 0,5. Углы наклона этой оси к горизонтальной линии могут приниматься 30°, 45° или 60°.

Расположение осей и изображения детали во фронталь­ной диметрии представлены на рис. 1.104, в.

В случае, когда существует необходимость сохранить без искажения фигу­ры, расположенные в горизонтальной плоскости проекций, аксоно­метрическую проекцию располагают параллельно горизонтальной плоскости проекций, и все коэффициенты искажения принимают равными единице. Полученная аксонометрическая проекция назы­вается горизонтальной изометрией, или иначе ее называют зенитной перспективой. Допускается применять изометрические проек­ции с углом наклона оси OY 45° и 30°, при сохранении прямого угла между осями ОХ и OY. На рис. 1.104, г, д изображена деталь в зенитной перспективе.

И

Рис. 1.105

зображение окружности в аксонометрических проекциях. При построении аксонометрических проекций машинострои­тельных деталей часто приходится иметь дело с построением аксо­нометрических проекций окружностей. В большинстве случаев ок­ружности лежат в плоскостях, параллельных какой-либо из коорди­натных плоскостей. Рассмотрим примеры построения окружностей в прямоугольных изометрической и диметрической проекциях.

Изобразим окружности, вписанные в грани куба. На рис. 1.105 представлены проекции куба в изометрии и диметрии.

Окружность, вписанная в грани куба, касается его ребер в их се­редине. Из свойств параллельного проецирования известно, что если точка на отрезке делит его длину в заданном отношении, то и проек­ция точки делит одноименную проекцию отрезка в том же отноше­нии. Значит, в аксонометрических проекциях точки касания эллипсов, в которые преобразуются окружности, будут находиться также в серединах ребер куба. Кроме этих четырех точек можно указать еще четыре. В прямоугольных проекциях направления большой оси эллипсов перпендикулярны свободным аксонометрическим осям, а малые оси совпадают с ними по направлениям.

Для изометрии величина большого диаметра эллипса равна 1,22d окружности, малого диаметра - 0,71d. В диметрии большой диаметр эллипса равен l,06d, а малый диаметр для эллипсов, расположен­ных в плоскостях, параллельных координатным плоскостям XOY и YOZ, равен 0,35d. Для эллипсов, расположенных параллельно плос­кости XOZ, малый диаметр равен 0,95d.

При построении аксонометрических изображений в изометри­ческой проекции, эллипсы можно заменить овалами и строить их, как показано на рис. 1.106.

Рассмотрим построение овала, лежащего во фронтальной плос­кости проекций. Выберем на фронтальной плоскости проекций точ­ку О, через которую проведем изометрические оси. Из точки О про­водим окружность радиуса R. Там, где эта окружность пересечет ось Oz, поставим точки 1 и 2, а где Ох - точки 3 и 4 . Из точки 1, как из центра, делаем засечку радиусом 2R на продолжении малой оси эл­липса и с

Рис. 1.106

тавим точку О₁, из точки 2 строим симметричную ей точку О₂. Из точки О₁, как из центра, проводим дугу gGg радиуса 2R, кото­рая является одной из дуг, определяющих контур овала. Для точки О₂ сделаем аналогичное построение. Из точки О, как из центра, про­водим дугу радиуса R₁ = OG до пересечения с большой осью эллип­са в точках О₁ и O₄. Через точки О₁ и О₃, а также О₁ и О₄ проводим прямые, получаем точки К и М, находящиеся на пересечении с ду­гой gGg, которые определяют R₂ = О₃К = О₄М - величину радиуса замыкающей дуги овала. Точки К и М являются точками сопряжения дуг, составляющих овал.

Построение овалов в диметрической проекции производится не­сколько иначе. Рассмотрим построение овала, лежащего во фрон­тальной плоскости проекций. (Рис. 1.107) Выберем на фронтальной плоскости проекций точку О, через которую проведем диметрические оси. Из центра О проводим окружность заданного радиуса R.

О

Рис. 1.107

на пересечет ось Оу в точке 1, а ось Оz в точке 2. Из точки 1, как из центра, проводим дугу радиуса R = 12. Эта дуга пересечет ось Оу в точке О₁. Из точки О радиусом R₂ = ОО₁ проводим окружность, кото­рая пересечет большую ось в точках О₂ и О₄ и малую в точке О₃. Через точки О₁ и О₄, а затем через точки О₂ и О₃, проводим лучи. Приняв за центр точки О₂ и О₄ радиусом R₃ = 3O₂ проводим малые дуги между лучами, выходящими из этих центров.

Приняв за центры точки O₁ и О₃, радиусом R₄ = О₁3 проводим большие замыкающие дуги. Построение овала закончено.

Построение в диметрии овала, лежащего в горизонтальной или профильной плоскости проекций, несколько отличается от преды­дущего. Построим овал в горизонтальной плоскости проекций. (Рис. 1.107) Выберем на горизонтальной плоскости проекций точку О, че­рез которую проведем диметрические оси, и проведем большую ось овала перпендикулярно оси OZ. Примем точку О за центр, из кото­рого проведем окружность радиуса 2R. Она пересечет ось OZ внизу в точке O₂, а вверху в точке O₁. Из точки О радиусом R проводим окружность, которая пересечет ось Ох в точках 1 и 2. Из центров O₁ и O₂ радиусом R₁=O₁1 = O₂2 проводим большие дуги овала. Затем проводим прямые, соединяющие точки 1 и O₁ и 2 и О₂. Они пересе­кут большую ось в точках O₁ и О₄. Приняв эти точки за центры, про­водим замыкающие овал малые дуги радиусом R = 1О₃ = 2О₄. Пост­роение овала, лежащего в профильной плоскости проекций, будет аналогично приведенному выше.

Построение аксонометрической проекции точки. Изображение любой геометрической фигуры в аксонометричес­ких проекциях включает построение аксонометрической проекции некоторого числа точек, определяющих эту фигуру, в частности, аксонометрическая проекция кривой линии сводится к построению точек, принадлежащих кривой, которые затем соединяют между со­бой при помощи лекал.

Р

Рис. 1.108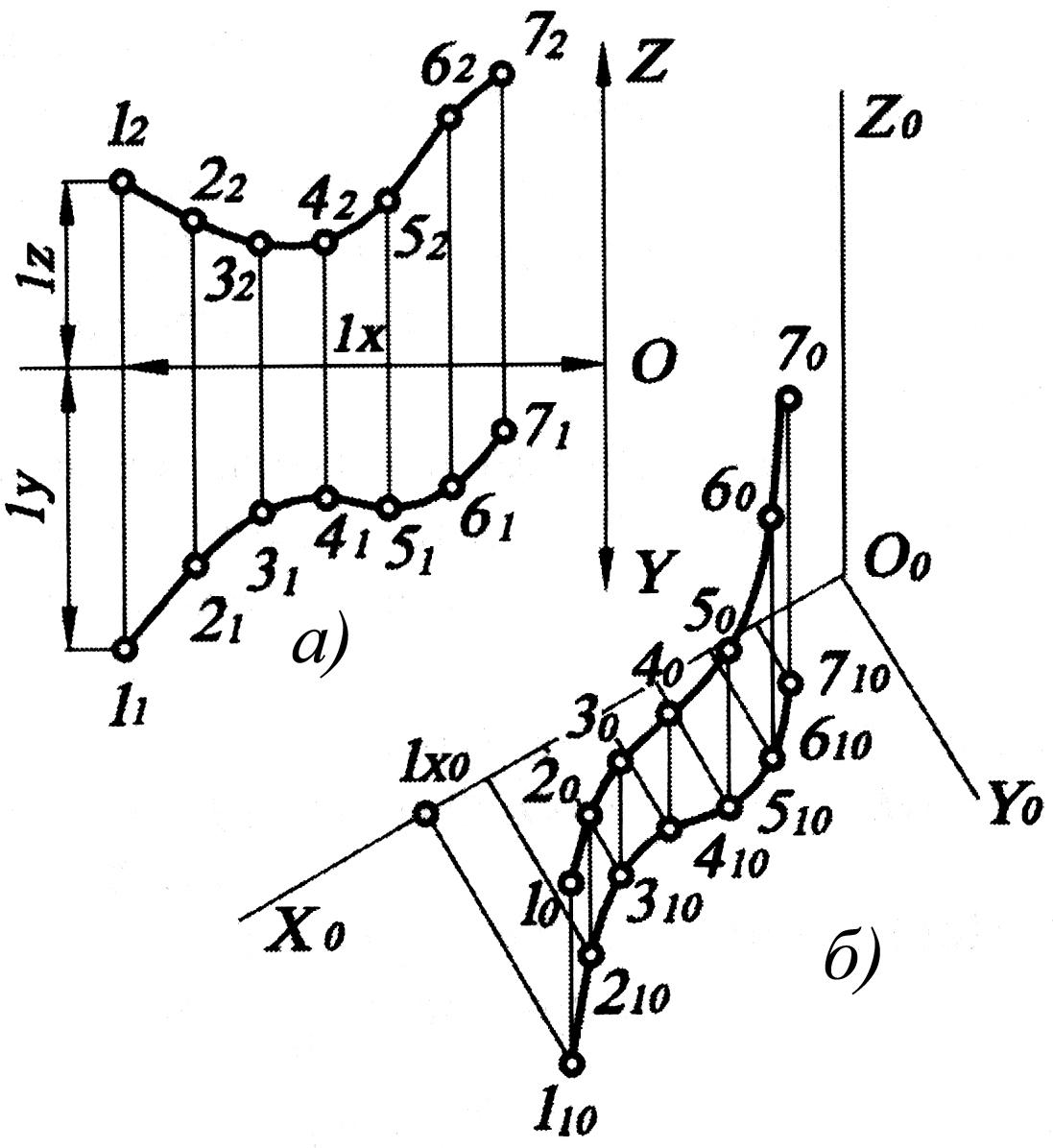

ассмотрим построение кривой l. Рас­сматриваемую кривую поместим в декартову систему координат (рис. 1.108, а). Отметим на кривой точки 1, 2, 3, … ,7. Построим горизонтальные 1₁, 2₁, 3₁, … ,7₁ и фронтальные 1₂, 2₂, 3₂, … ,7₂ проек­ции точек, каждая из которых определяется тремя координатами х, у, z.

Проведем аксонометрические оси проекций. Рассмотрим пост­роение аксонометрической проекции одной из точек, лежащих на кривой l.

Определим координаты точки 1 относительно декартовой систе­мы координат (см. рис. 1.108, а). После чего построим аксонометри­ческую проекцию точки 1. От начала координат, точки О₀, отклады­ваем по оси О₀X₀, координату х и ставим точку 1_0x. Через полученную точку параллельно оси О₀Y₀ проводим прямую, на которой откладываем координату у точки 1 и ставим точку 1₁₀. Полученная точка является вторичной проекцией точки 1. Чтобы получить непосредствен­но аксонометрическую проекцию точки, из точки 1₁₀ проводим пря­мую, параллельную оси O₀Z₀, на которой откладываем аппликату точки 1. Получаем точку 1₀.

Построение аксонометрических проекций точек 2, 3, 4,…,7 про­изводим аналогично (см. рис. 1.108, б). Соединив найденные аксономет­рические проекции точек 1₀, 2₀, 3₀, …, 7₀ плавной линией, получаем аксонометрическую проекцию l₀ кривой l.

Построение аксонометрических проекций многогранников. Построение аксонометрических проекций необходимо выполнять с использованием рациональных приемов построения, чтобы избе­жать лишней работы. Обычно изображение начинают строить с ха­рактерной части предмета, а затем последовательно пополняют его недостающими элементами.

Рассмотрим порядок построения изометрической проекции вось­мигранной призмы с вырезами.

И

Рис. 1.109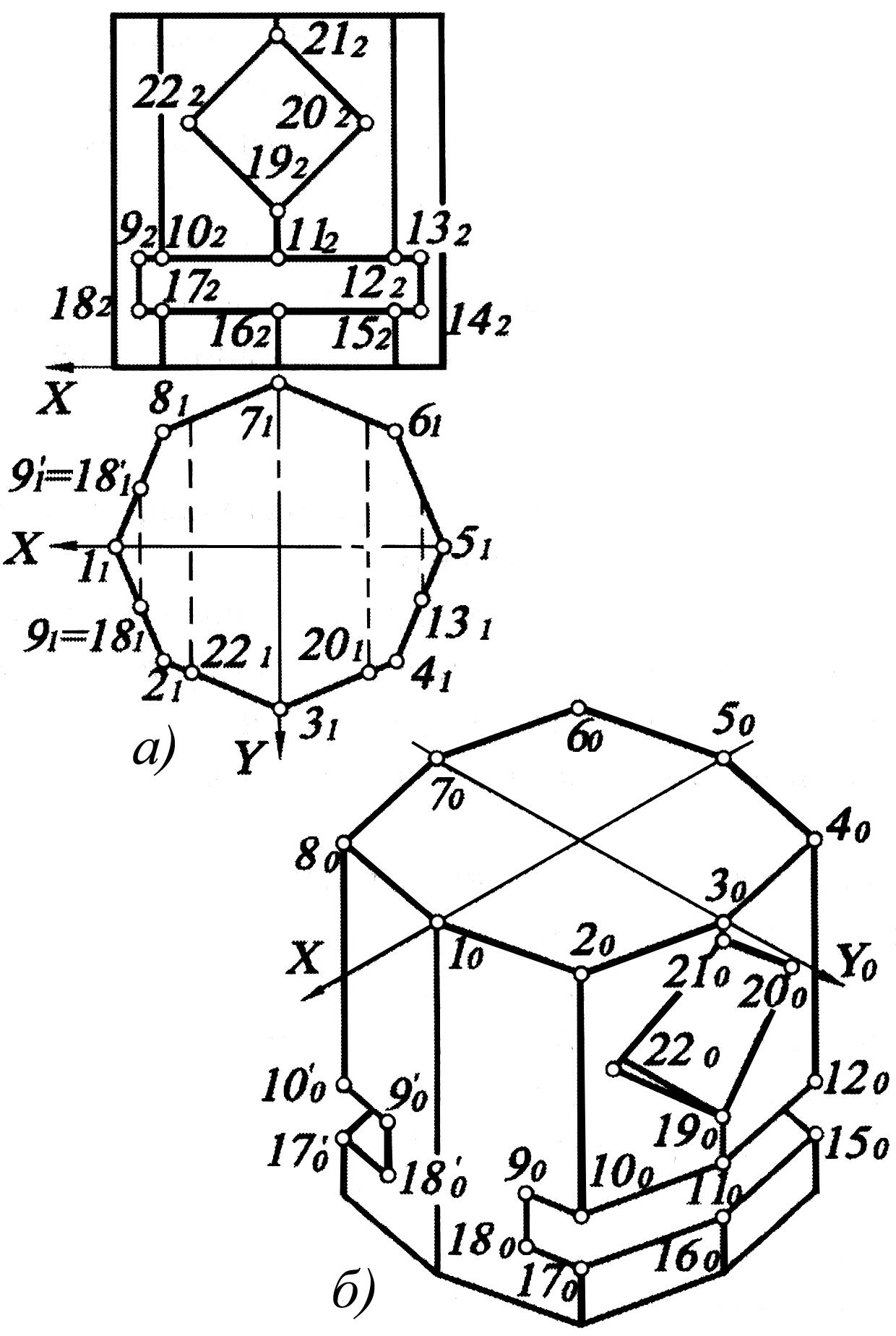

зображение призмы удобно начинать с верхнего видимого ос­нования Изометрическая проекция восьмиугольника вычерчивает­ся по координатам его вершин Отметим, что каждый отрезок, на­правленный по осям OX, OY, OZ или параллельный им, сохраняет свою величину

Обозначим вершины верхнего основания призмы 1, 2, 3, 4, 5, 6, 7, 8. Определим положение призмы относительно декартовой систе­мы координат. (Рис. 1.109, а) Определим координаты x и у вершин основания. Проведем аксонометрические оси проекций. На них по­строим точки 1₀, 2₀, 3₀, 4₀, 5₀, 6₀, 7₀, 8₀. Полученные точки верхнего основания соединяем между собой.

Нижнее основание призмы смещено вниз на высоту призмы. По­этому, откладывая эту величину из вершин восьмиугольника парал­лельно оси OZ и соединяя концы отложенных отрезков, получим изображение призмы.

Вырезы на гранях призмы будем строить по характерным точкам. Это точки 9, 10, 11, 12, …, 18 для прямоугольного выреза и для квад­ратного выреза 19, 20, 21, 22. Выбранные точки по заданным коорди­натам можно построить на поверхности восьмигранной призмы. После чего, соединив последовательно полученные аксонометрические про­екции точек, получим искомые очертания вырезов. (Рис. 1.109, б)

П

Рис. 1.110

Рис. 1.111

остроение прямоугольной изометрической проекции детали. Если деталь или изделие показывают с разрезом, то во многих случаях целесообразно начинать построение с вычерчивания всех контурных линий сечения детали в плоскости разреза. При этом отпадает необходимость изображения «вырезанной» части пред­мета.

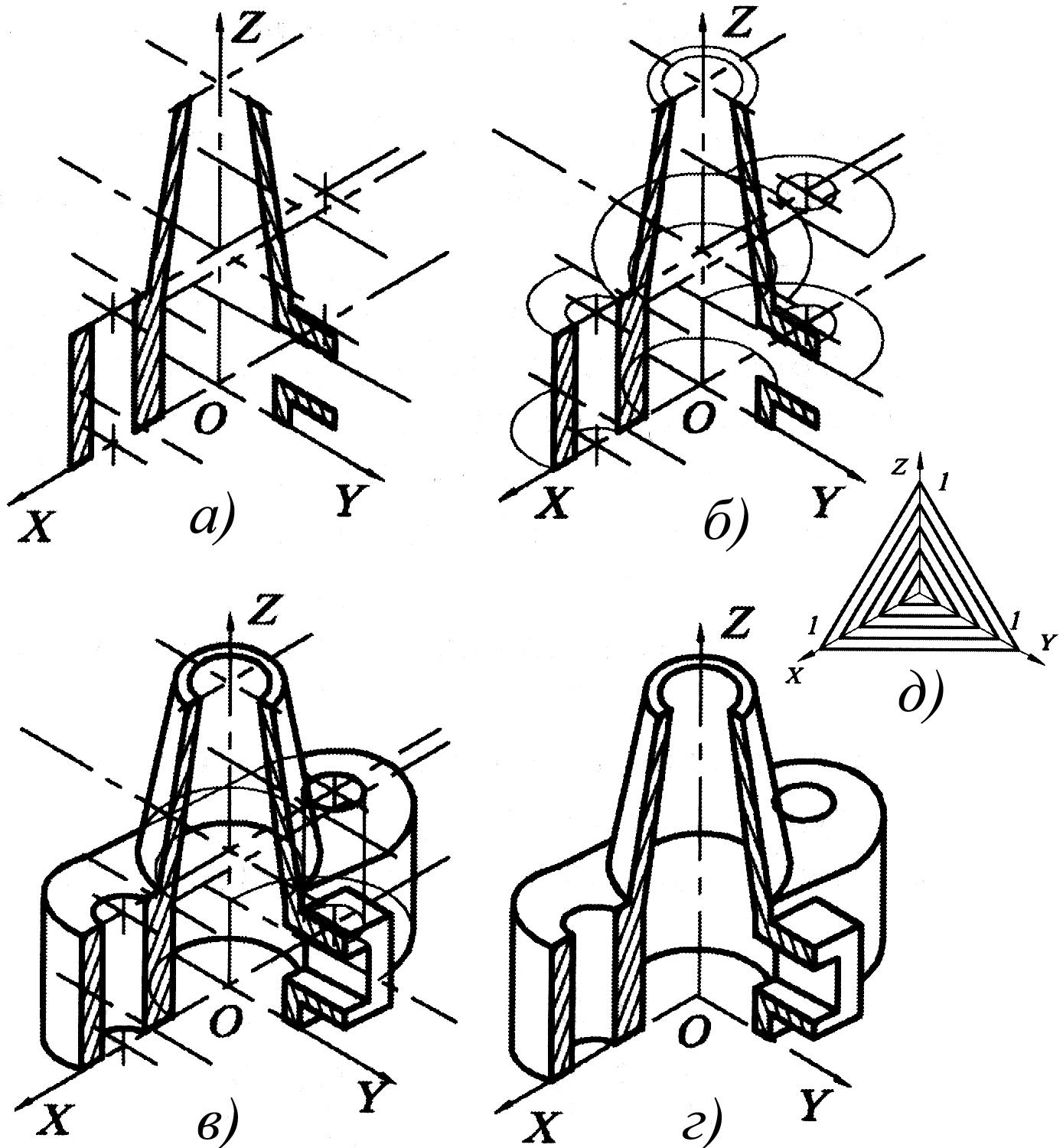
Соотнесем деталь с декартовой системой координат и нанесем на комплексный чертеж детали проекции координатных осей. (Рис. 1.110)

Построим аксонометрические оси и аксонометрические проекции сечений выреза координатными плоскостями XOZ и YOZ и од­новременно с этим нанесем аксонометрические проекции центров всех окружностей. (Рис. 1.111, а)

Построим эллипсы, являющиеся проекциями окружностей ос­нований цилиндров и конусов, ограничивающих отдельные части детали. (Рис. 1.111, б)

Построим прямолинейные очертания детали и обведем линии видимого контура. (Рис. 1.111, в)

Окончательный вид детали см. рис. 1.111, г.

Наклон линий штриховки в разрезах принимается для изометри­ческой проекции согласно схеме, представленной на рис. 1.111, д.

П

Рис. 1.112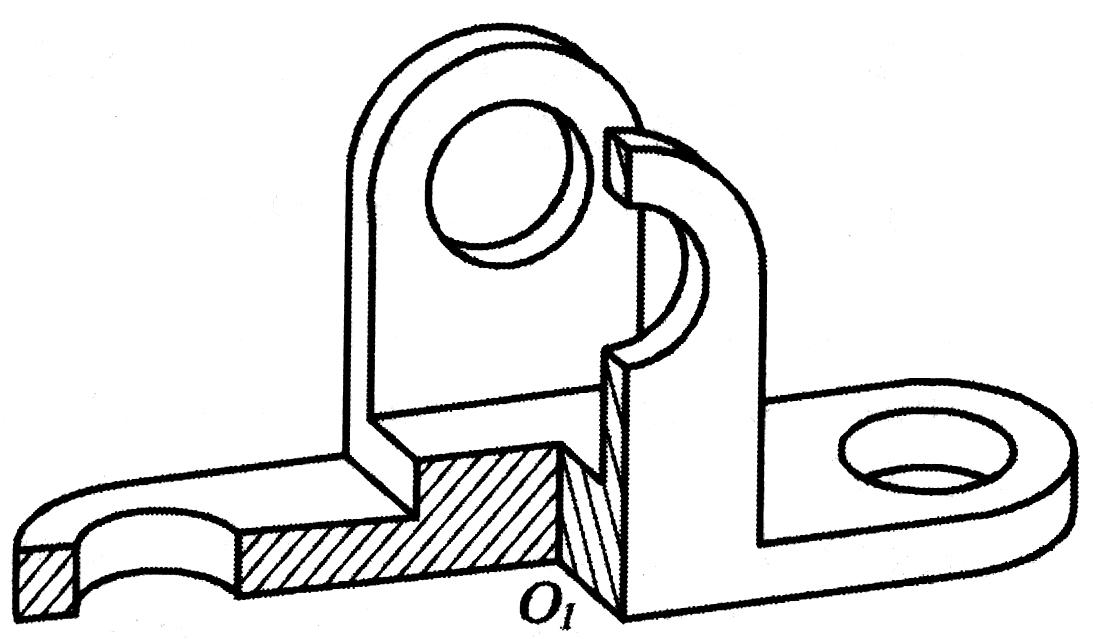

остроение прямоугольной диметрической проекции. Порядок построения прямоугольной диметрической проекции ничем не отличается от построения прямоугольной изометрии, но при этом нужно только учитывать, что коэффициент искажения по оси OY= 0,5. Если вычерчивают деталь с разрезом, то выполнение диметрии заканчивают штриховкой разрезанных стенок. (Рис. 1.112) Направление штриховки принимают согласно аналогичной схеме.

Контрольные вопросы для самопроверки

1. Как строят центральную проекцию точки?

2. В каком случае центральная проекция прямой линии является точкой?

3. Чем отличается метод параллельного проецирования от метода центрального проецирования?

4. Как строят параллельную проекцию прямой линии?

5. Может ли параллельная проекция прямой линии представлять со­бой точку?

6. В каком случае при параллельном проецировании отрезок прямой линии проецируется в натуральную величину?

7. Как расшифровывается понятие "ортогональный"?

8. Как читается свойство проецирования прямого угла?

9. Что такое эпюр Монжа?

10. Что такое система П₁, П₂, П₃ как называют плоскость проекции П₃.

11. Как строят профильную проекцию точки по ее фронтальной и го­ризонтальной проекциям?

12. Что такое прямоугольные координаты точки и в какой последова­тельности их записывают в обозначении точки?

13. Что такое октанты?

14. В каком октанте значения координат по всем осям отрицательные? Как на прямой линии определить точку, равноудаленную от плоскостей П₁ и П₂? На какой прямой такой точки не существует?

15. Может ли ортогональная проекция острого угла быть тупым углом, а тупого — острым?

16. Могут ли проекции скрещивающихся пря­мых быть параллельными?

17. 6. В каком случае проекции прямого угла на плоскости П₁ и П₂ равны 90°?

18. На прямой, определяемой точками А (10; 30; 10) и В (60; 10; 50), построить отрезок АС длиной 45 мм.

19. Задавшись горизонтальной проекцией от­резка АВ прямой общего положения и его дли­ной, построить фронтальную проекцию А₂В₂.

20. Определить расстояние от точки А (20; 40; 50) до каждой из координатных осей.

21. При каком положении относительно плоскостей проекций прямую называют прямой общего положения?

22. Как выражается соотношение между проекцией отрезка прямой и самим отрезком?

23. Как расположена прямая в системе П₁, П₂, П₃, если все три проекции отрезка этой прямой равны между собой?

24. Как построить профильную проекцию отрезка прямой общего по­ложения по данным фронтальной и горизонтальной проекциям?

25. Как располагается фронтальная проекция отрезка прямой линии, если его горизонтальная проекция равна самому отрезку?

26. Как располагается горизонтальная проекция отрезка прямой линии, если его фронтальная проекция равна самому отрезку?

27. Как разделить на чертеже отрезок прямой линии в заданном отно­шении?

28. Как построить на чертеже треугольники для определения длины отрезка прямой линии общего положения и ее углов с горизонталь­ной и фронтальной плоскостями проекций?

29. Какое свойство параллельного проецирования относится к парал­лельным прямым?

30. Можно ли по фронтальной и горизонтальной проекциям двух про­фильных прямых определить, параллельны ли между собой эти прямые?

31. В каком случае прямой угол проецируется в виде прямого угла?

32. Что называют следом плоскости на плоскости проекций?

33. Где располагаются фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа плоскости?

34. Как определяют на чертеже, принадлежит ли прямая плоскости?

35. Как строят на чертеже точку, принадлежащую плоскости?

36. В чем заключается общий способ построения линии пересечения двух поверхностей?

37. Какие точки линии пересечения поверхностей называют характер­ными?

38. В каких случаях для построения линии пересечения одной поверх­ности другой рекомендуется применять вспомогательные секущие плоскости, параллельные плоскостям проекций?

39. В каких случаях возможно и целесообразно применять вспомогатель­ные секущие сферы?

40. По каким линиям пересекаются между собой цилиндрические поверхности, образующие которых параллельны между собой?

41. Какие линии пересечения получаются при взаимном пересечении двух поверхностей вращения, описанных вокруг общей для них сферы?

42. По каким линиям пересекаются между собой соосные поверхности вращения?

43. В чем заключается способ аксонометрического проецирования?

44. Что называют коэффициентами (или показателями) искажения?

45. В каких случаях аксонометрическую проекцию называют: а) изометрической; б) диметрической; в) триметрической?

46. Как определяют направление и величину малой оси эллипса, явля­ющегося изометрической или диметрической проекцией окружнос­ти, расположенной в плоскостях: общего положения; фронталь­но-проецирующей и горизонтально-проецирующей; фронтальной, горизонтальной и профильной?

Список лиературы

1. Брилинг Н.С. Черчение. - М.: Стройиздат, 1989. - 420 с.

2. Бубенников А.В. Начертательная геометрия. - М.: Высшая школа, 1985. - 288 с.

3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учебн. Пособие/ Под ред .Ю.Б. Иванова. – 23-е изд.,перер. – М.: Наука, 1988. -272 с.

4. Гордон В.О., Семенцов-Огиевский М.А. Курс начертатель­ной геометрии. Учебное пособие. — М.: Высшая школа, 1998. — 272 с.

5. Государственные стандарты ЕСКД: ГОСТ 2.301—68* — ГОСТ 2.307-68*; ГОСТ 2.308-79; ГОСТ 2.309-73; ГОСТ 2.310-68*; ГОСТ 2.311-68*; ГОСТ 2.312-72; ГОСТ 2.313-82; ГОСТ 2.316-68*; ГОСТ 2.317-69 Государственные стандарты системы проектной документации для строительства (СПДС); ГОСТ 21.001—77 (общие положения); ГОСТ 21.101—79 (основные требования к рабочим чертежам); ГОСТ 21.102—79 (общие данные по рабочим чертежам); ГОСТ 21.103—78 (основные надписи); ГОСТ 21.104—79 (спецификации); ГОСТ 21.105—79 (нанесение на чертежах размеров, надписей, технических требований и таблиц); условные изображения и обозначе­ния: ГОСТ 21.106-78 (трубопроводов); ГОСТ 21.107-78 (элементов зданий); ГОСТ 21.108-78 (на генеральных планах); ГОСТ 21.501—80 (архитектурные решения, рабочие чертежи).

6. Короев Ю.И. Начертательная геометрия: Учебник для вузов. – М.: Стройиздат, 1987. – 319 с.

7. Локтев О.В. Краткий курс начертательной геометрии — М.: Высшая школа, 1998. — 192 с.

8. Посвянский А.Д. Краткий курс начертательной геометрии. – М.: Высшая школа, 1974. – 192 с.

9. Соломонов К.Н., Бусыгина Е.Б., Чиченева О.Н. Начертательная геометрия: Учебник для вузов. – М.: МИСИС, 2003. -160с.

10. Фролов С.А. Начертательная геометрия. - М.: Машиностроение, 1983.-240 с.

11. Чекмарев А.А. Начертательная геометрия и черчение: учеб. для студ. высш. учеб. заведений/А.А. Чекмарев. — 2-е изд., перераб. и доп. — М.: Гуманитар, изд. центр ВЛАДОС, 2005. — 471 с. : ил.