1.7. Поверхности вращения.

Кривая линия отличается от прямой тем, что длина отрезка (уча­стка) кривой линии, соединяющей две любые точки на ней, не явля­ется кратчайшим расстоянием между этими точками.

Кривую линию можно рассматривать как траекторию движения точки в пространстве или как множество точек, расположенных в пространстве в соответствии с некоторым законом. Кривая линия может быть получена как результат пересечения плоскостью кривой поверхности или кривых поверхностей между собой.

Кривая линия называется плоской, если все составляющие ее точ­ки лежат в одной плоскости, и пространственной - в противном слу­чае. К плоским кривым относятся, например, окружность, эллипс, ги­пербола, парабола кривые второго порядка, полученные в результа­те пересечения боковой поверхности конуса плоскостью, наклоненной к основанию конуса под разными углами. Примерами пространствен­ных кривых служат винтовая линия, линия пересечения боковой по­верхности конуса и сферы, оси которых не совпадают.

Для того чтобы построить проекцию кривой линии, необходимо знать координаты достаточного количества ее точек. Чем менее плав­ная кривая, чем больше изгибов она содержит, тем большее количе­ство точек нужно выбрать на ней для ее точного определения в про­странстве, а, следовательно, и построения ее проекций. И пространственная и плоская кривые проецируются на плос­кость в виде плоской кривой, либо в виде прямой, если плоскость, в которой расположена кривая, является проецирующей по отноше­нию к соответствующей плоскости проекций.

При проецировании кривых существенным является тот факт, что проекция кривой некоторого порядка сохраняет тот же порядок (т.е. имеет такой же вид) или оказывается кривой более низкого по­рядка. Так, эллипс и окружность проецируются в эллипс или, в час­тном случае, в окружность, если проецируемая окружность распо­ложена в плоскости, параллельной плоскости проекций, проекция параболы - парабола, гиперболы - гипербола.

Для определения натуральной величины кривой необходимо за­менить ее ломаной, точ­ки излома которой соот­ветствуют точкам изги­ба кривой линии.

Рассмотрим решение этой задачи на примере.

П

Рис. 1.75

усть заданы фрон­тальная и горизонталь­ная проекции кривой АВС. (рис. 1.75) Необхо­димо определить ее на­туральную величину.

Для этого развернем пространственную кри­вую на плоскости. Вы­бираем некоторое коли­чество характерных то­чек 1,2, 3, 4, 5, 6, 7, где кривая имеет значительные участки кривой между этими точками на отрез­ки прямой, незначитель­но исказив тем самым их длину.

Сведем задачу к построению отрезков ломаной линии, соеди­няющих обозначенные точки. Измеряем последовательно расстоя­ния между точками A₁ и 1₁, 1₁ и 2₁, 2₁ и 3₁ и т.д. и откладываем на оси OX от произвольно выбранной точки А₁*. Затем на пересечении горизонтальных и вертикальных прямых, проведенных соответ­ственно из A₁* и А₂, 1₁* и 1₂, 2₁* и 2₂ и т.д., построим точки А₀, 1₀, 2₀ ... и т.д. Соединив эти точки прямыми линиями, получаем лома­ную линию А₀1₀2₀ ...С₀, которая и определит натуральную величи­ну кривой ABC. Очевидно, что длина этой ломаной меньше длины пространственной кривой АВС. Полученная ломаная линия тем ближе по длине к заданной кривой, чем большее количество про­межуточных точек на ней нами выбрано.

В качестве примера построения проекций пространственной кривой рассмотрим винтовую линию. Цилиндрическая винтовая линия представляет собой траекторию движения точки, совершающей равномерное вращательно поступательное движение о

Рис. 1.76

тносительно оси цилиндра по его поверхности. На рис. 1.76 она обозначена АВСВ*С*В*.

Расстояние между соседними витками Р называется шагом вин­товой линии, а расстояние от любой точки на винтовой линии до оси цилиндра - радиусом R винтовой линии. Очевидно, что для опреде­ления положения винтовой цилиндрической линии в пространстве вполне достаточно этих двух параметров.

П

Рис. 1.77

остроим проекции одного витка винтовой линии радиуса R и шагом Р. Если винтовая линия расположена на поверхности прямого кругового цилиндра, ось которого явля­ется горизонтально-проецирующей ли­нией, тогда горизонтальная проекция винтовой линии представляет собой ок­ружность радиуса R, поскольку боковая поверхность цилиндра, на которой ле­жит винтовая линия, в этом случае проецируется на П₁ в окружность. (Рис. 1.77) Так как винтовая линия является траекторией точки, движущейся равномер­но по окружности и вдоль оси, то рас­стояние между соседними точками на П₁ и на П₂ вдоль оси цилиндра должно быть одинаковым. Тогда необходимо разбить окружность и прямоугольник, служа­щий фронтальной проекцией цилиндра, на одинаковое количество частей. Чтобы разделить окружность, например, на двенадцать частей, достаточно цирку­лем из точек 1₁, 4₁, 7₁ , 10₁, лежащих на осях, радиу­сом R провести дуги до пересечения с окружнос­тью.

Эти точки и являют­ся промежуточными. За­тем на пересечении вертикальной линии связи, проведенной из каждой точки на П₁, и соответ­ствующей горизонталь­ной прямой, которыми разделен прямоугольник, получаем фронтальную проекцию каждой из обо­значенных точек.

Соединив точки 1₂, 2₂, 3₂, 4₂ … 13₂ плавной кривой, имеем фронтальную про­екцию винтовой линии. От точки 7₂ до точки 13₂ она изображена пункти­ром, так как расположена на невидимой поверхности цилиндра.

Винтовая линия может быть получена вращением точки как по часовой стрелке, так и в противоположном направлении, при ее дви­жении по цилиндрической поверхности. В случае, когда подъему по винтовой линии соответствует движение по часовой стрелке на П₁, винтовую линию называют левой, в противном – правой. В рассмот­ренном примере (рис. 1.77) изображена правая винтовая линия.

В начертательной геометрии поверхность рассматривается как множество последовательных положений некоторой линии - обра­зующей поверхности, перемещающейся в пространстве определен­ным образом по другой линии, которую называют направляющей. В результате чего образуются кривые поверхности.

Образующая поверхности в процессе движения может изменять свою форму. Одна и та же поверхность может быть образована пере­мещением различных линий.

Кривые поверхности можно разбить на классы линейчатые, винтовые, циклические, поверхности вращения.

П

Рис. 1.78

оверхности вращения образуются при вращении некоторой произвольной линии вокруг оси. В этом случае образующей являет­ся указанная линия, а направляющей – окружность. Форма поверх­ности вращения определяется формой образующей.

Пусть произвольная линия ABС вращается вокруг оси i. Тогда она образует поверхность вращения. (Рис. 1.78)

Линия пересечения поверхности вращения плоскостью (образующая), прохо­дящей через ось z, называется меридианом (например, A*B*С*).

Меридиан, лежащий в плоскости, параллельной П₂ называется глав­ным. Линия пересечения поверхности вращения плоскостью, пер­пендикулярной оси i, называется параллелью. Таковыми являются направляющие, проходящие через точки АA*, ВB*, СС*. Парал­лель, проходящая через наиболее удаленную от оси точку С образу­ющей, называется экваторам, а через самую близкую точку В – горлом. Очевидно, что все параллели представляют собой окружности.

О

Рис. 1.79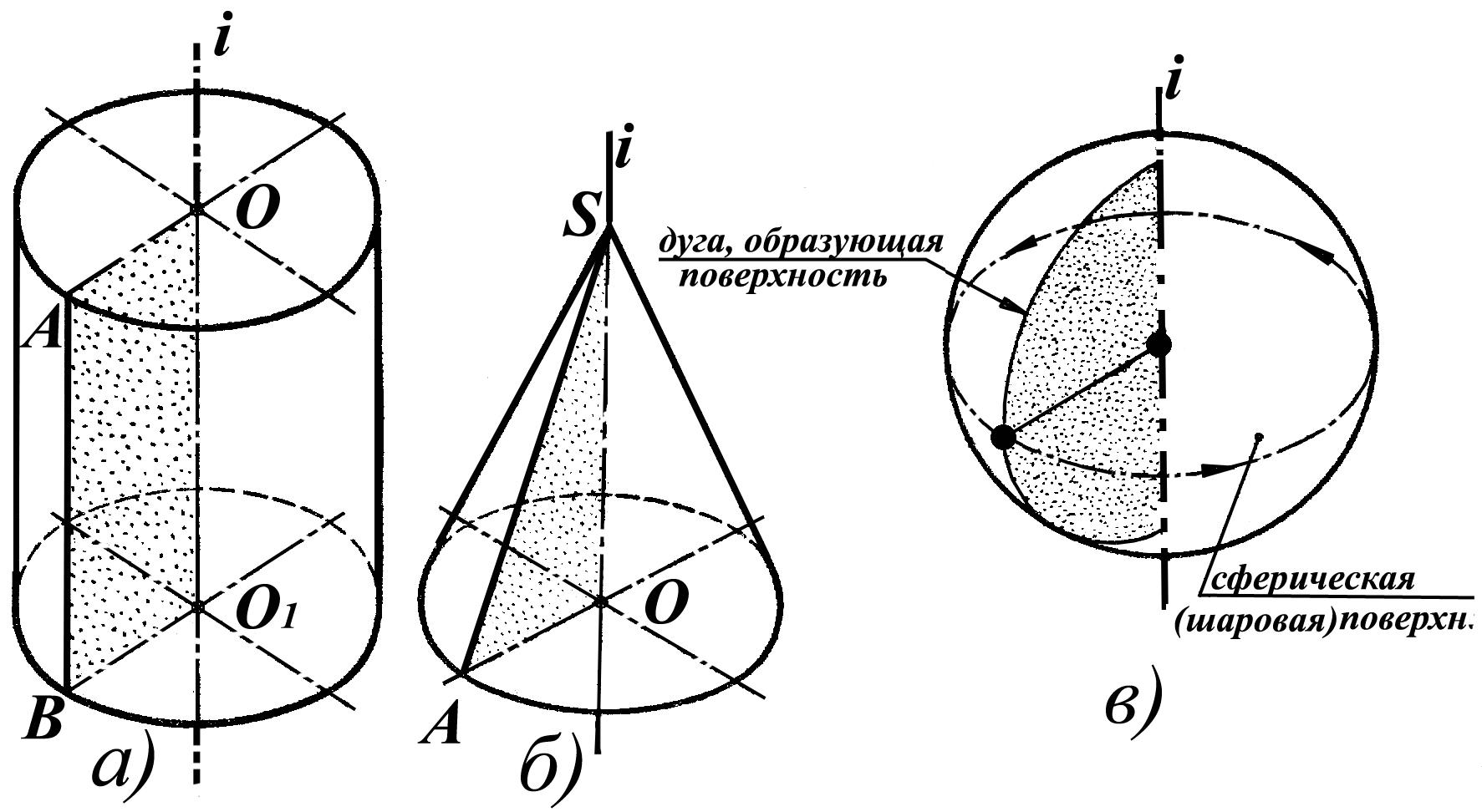

дной из самых простых поверхностей вращения является ци­линдр. Цилиндрическая поверхность образуется при вращении пря­мой (образующей) АВ вокруг оси. (Рис. 1.79, а) Образование цилинд­рической поверхности подобно получению призматической с той лишь разницей, что у гранной поверхности направляющей является ломаная линия

В случае образования конической поверхности прямая AS, вращающаяся вокруг оси, закреплена в некоторой точке S на оси (рис 1.79, б). Такая поверхность подобна пирамидальной, у которой образующей является тоже прямая, но перемещающа­яся по ломаной линии. Для того чтобы получить соответствующую повер­хность ограничить плос­костями основания.

Если в качестве обра­зующей выбираем окруж­ность, то при ее вращении вокруг оси получаем:

-

Рис. 1. 80

сферу, когда ось вращения проходит через центр О окружности (рис. 1.79,в),

- тор (рис. 1.80).

Если ось вращения проходит через образую­щую-окружность, тор получается закрытым (рис. 1.80, а), в против­ном случае открытым (рис. 1.80, б).

Рассмотрим построение проекций точки и линии на поверхностях вращения.

Цилиндр. Пусть задан прямой цилиндр, плоскости основания которого па­раллельны плоскости П₁. (Рис. 1.81)

Зная фронтальные проекции точек А и В, лежащих на боковой поверхности цилиндра построим отсутствующие проекции.

П

Рис. 1. 81

оскольку на П₁ боковая поверхность цилиндра проецируется в окружность, то А₁и В₁ лежат, очевидно, на ней. Их положение нахо­дим по вертикальным линиям связи. Профильные проекции A₃, В₃ лежат, как известно, на горизонтальных линиях связи с фронталь­ными проекциями А₂ и В₂. При этом, в соответствии с правилами ортогонального проецирования, расстояние от Ф₃ до профильной проекции точки равно расстоянию от Ф₁ до горизонтальной проекции точки. Причем точка В₃ - невидимая, так как лежит на невиди­мой части боковой поверхности цилиндра.

По заданной фронтальной проекции А₂В₂ (см. рис. 1.81) по­строим отсутствующие проекции.

Горизонтальная проекция А₁В₁ совпадает с окружностью, так как все точки линии АВ лежат на боковой поверхности цилиндра.

При построении профильной проекции А₃В₃ следует иметь в виду, что линия АВ пересекает прямую CD, которая на П₃ является конту­ром С₃D₃ цилиндра. Поэтому сначала следует определить положение контурной точки 1₃, а затем соединить точки А₃ и В₃ линией, которая в отличие от А₂1₂В₂ не является прямой. В связи с этим для построения необходимо на А₂1₂В₂ выбрать несколько промежуточных точек (2₂,3₂ и т.д.) и построить их профильные проекции (2₃, 3₃ и т.д.), руковод­ствуясь вышеуказанным правилом взаимосвязи проекций (горизон­тальной и профильной). Чем большее количество промежуточных точек выбираем, тем более точными будут построения.

Конус. Решим те же задачи построения проекций точки и линии, лежа­щих на поверхности конуса. (Рис. 1.82)

П

Рис. 1. 82

остроить отсутствующие проекции точек А и В расположенных на поверхности прямого кругового конуса, если известно поло­жение А₂ и В₂.

Для построения горизонтальной проекции точки А необходимо через ее фронтальную проекцию провести горизонтальную линию (параллель). Тогда на П₁ эта линия 12 представляет собой дугу окружности диа­метром 1₂2₂ = 1₁2₁. По линии связи на ней находим A₁. Аналогично, провода дугу окружности радиусом S₁3₁ равным расстоянию от оси конуса до точки 3₂ на его контуре, определяем положение на ней точки B₁. По этим проекциям находим положение А₃, В₃.

По известной проекции А₂В₂ линии АВ, лежащей на поверхнос­ти конуса, построить горизонтальную и профильную проекции.

Выбрав на линии А₂В₂ промежуточную точку 4₂, найдем 4₁ так же, как сделали это для точек А и В. Соединив точки А₁, 4₁, В₁, полу­чим горизонтальную проекцию линии АВ.

Для построения профильной проекции А₃В₃ необходимо найти положение контурной точки 4, лежащей на SE.

По фронтальной проекции 4₂, лежащей на S₂Е₂, находим профильную проекцию 4₃, ле­жащую на S₃E₃. Теперь точки A₃, 4₃, B₃ можно соединить линией.

При соединении точек линией всегда надо руководствоваться правилом: для каждой проекции точки, принадлежащие линии, следует соединять в одинаковой после­довательности. Так, если на фронтальной проекции точка 4 яв­ляется промежуточной, то она будет промежуточной и на дру­гих проекциях.

С

Рис. 1. 83

фера. Проекцией сферы на любую плоскость проекций является ок­ружность.

Рассмотрим построение проекций точек на поверхности сфе­ры. (Рис. 1.83).

Задача состоит в том, чтобы по известным проекциям построить отсутствующие. Обозначим все необходимо характерные точки сферы.

Точки, лежащие на экваторе, обозна­чим через А, В, С, D; точки, лежащие на главном меридиане - А, Е, С, F. Очевидно, что точки А и С принадлежат одновременно и эква­тору и главному меридиану.

При построении проекций следует иметь в виду, что любая па­раллель на П₂ проецируется в горизонтальную прямую, а на П₁ — в окружность.

Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П₂ получим горизонтальную прямую, про­ходящую через точку М₂. А на П₁ - дугу окружности радиусом F₁1₁, равным расстоянию от вертикальной оси до точки 1₂. Ясно, что точ­ка М₁ лежит на этой окружности. По двум проекциям М₁ и М₂, ис­пользуя правило взаимосвязи проекций, построим М₃.

Рассмотрим другую точку N, проекция которой N₂ на П₂ являет­ся невидимой. Аналогично предыдущему построим N₁, лежащую на дуге окружности радиусом F₁2₁. Так как N₂ - невидимая, то N₁ лежит выше оси Ф₁. А поскольку точка N находится на поверхности ниж­него полушария, что видно из положения N₂, то N₁ – невидимая. Профильная проекция N₃ строится по известному правилу взаимосвязи проекций. При этом, так как N₁ лежит выше оси Ф₁, то N ₃ - левее Ф₃. Поскольку точка N лежит в правом полушарии, то на П₃ она невиди­мая, так как на П₃ все правое полушарие закрыто от нас левым и является невидимым.

Видимость и невидимость полушарий, а, следовательно, и точек, лежащих на них, можно легко определить, рассматривая с разных точек зрения обыкновенный резиновый мячик, нарисовав на нем экватор и два меридиана, расположенных в плоскостях, перпенди­кулярных друг другу.

Построим горизонтальную и профильную проекции линии MN, если известна ее фронтальная проекция M₂ N₂, состоящая из прямо­линейных отрезков М₂3₂ и 3₂N₂.

Очевидно, что точка 3₁ лежит на A₁Е₁, так как 3₂ - на А₂Е₂. При этом прямая MN проходит через экватор (точка 4₂). Следовательно, на П₁- через точку 4₁. А участок 4₁3₁ - невидимый, поскольку, как видно по его фронтальной проекции 4₂3₂, он лежит в нижнем полу­шарии, т. е. ниже экватора.

Для построения проекций участка 3N выберем промежуточную точку 5₂. Тогда точка 5₁ лежит на дуге окружности радиуса 5₂6₂. Со­единив точки 3₁, 5₁, N₁ получим искомую линию M₁4₁3₁5₁N₁.

Построим профильную проекцию N₃М₃, которая проходит через те же промежуточные точки. Так как М₂3₂ вертикальная прямая, то на П₃ она представляет собой дугу М₃3₃ окружности радиуса 4₂3₂ = А₃3. Точка 5₃ - контурная для профильной проекции сферы. Значит, остается соединить точки 3₃, 5₃, N₃ кривой линией. При этом участок 5₃N₃ – невидимый.

Если необходимо более точное построение проекций линии MN, тогда на всех участках, где ее проекции не являются от­резками прямой или окружности, необходимо выбрать несколько промежуточных точек.

Т

Рис. 1. 84

ор. Рассмотрим открытый тор, ось которого расположена вертикаль­но, т. е. является горизонтально-проецирующей линией. Учитывая, что построение профильной проекции не вызывает больших затруднений, построим проекции лишь на П₁ и П₂. (Рис. 1.84)

Обозначим на рис. 1.84 характерные точки А, В, С, D, Е, F, G, К, L, G*, К*, L*. Теперь рассмотрим переднюю половину поверхности тора.

По горизонтальным проекциям точек М и N построить фрон­тальные. Для этого необходимо через точки М₁ и N₁ провести дуги окруж­ности радиуса O₁M₁ и O₁N₁ соответственно до пересечения с прямой А₁В₁, где получим точки 1₁ и 2₁. По линиям связи построим точки 1₂ и 2₂, лежащие на окружностях, образующих поверхность тора. Че­рез них проведем горизонтальные прямые, соответствующие дугам окружности на П₁. Следовательно, на них лежат точки М₂ и N₂. Так как контуром видимости является линия GLK, то точка М₂ - невиди­мая, а N – видимая.

Построим фронтальную проекцию линии MN, горизонтальная проекция которой представляет собой прямую М₁N_1.

Точка 3₁, принадлежащая М₁N₁ , лежит на контуре. Значит, ее по­ложение на K₂L₂ можно получить по линии связи через 3₁. Очевид­но, участок между точками N₂, 3₂ видимый, а между 3₂ и М₂ - неви­димый. Так как невидимый участок достаточно протяженный, выбе­рем дополнительную промежуточную точку 4₁. Ее фронтальную проекцию 4₂ построим аналогично точкам М и N, проведя дугу окружности радиуса 0₁4₁. Далее, соединив точки М₂, 4₂, 3₂, N₂, получаем решение нашей задачи. Кривая М₂ N₂ и видимого 3₂N₂ участков.

Рассмотрим задачи на определение общих геометрических эле­ментов при пересечении поверхностей вращения другими геометрическими объектами и между собой.

Пересечение поверхности вращения прямой. Для отыскания точек пересечения прямой с поверхностью вра­щения применим уже описанный ранее метод вспомогательной се­кущей плоскости, которая должна быть проведена через рассматриваемую прямую.

П

Рис. 1. 85

усть требуется построить фронтальную и горизонтальную проекции точек пересечения прямой а с конусом. (Рис. 1.85)

Проведем через прямую а горизонтально-проецирующую плос­кость . Тогда их горизонтальные проекции a₁ и ₁ совпадут.

Построим линию пересечения плоскости  и конуса. На плоско­сти горизонтальная проекция этой линии совпадает с a₁ и ₁.

Для тою, чтобы построить фронтальную проекцию этой линии, достаточно определить положение проекций нескольких точек. На П₁ выберем точки 1₁, 2₁, лежащие на основании конуса, точку 3₁, распо­ложенную на образующей S₁В₁, и промежуточную точку 4₁. Все эти точки лежат на боковой поверхности конуса, поэтому для их постро­ения используют правила построения точек на поверхности. А имен­но, точки 1₂, 2₂, 3₂ получаем по линиям связи. Некоторые сложности составляет лишь построение точки 4₂. Из вершины S₁ конуса радиусом S₁4₁ проводим дугу ок­ружности до пересечения с образующей S₁A₁ в точке 5₁. Затем по линии связи на S₂A₂ строим точку 5₂. Про­ведя через нее горизон­тальную прямую, на ли­нии связи с 4₁ получаем точку 4₂. Соединив точки 1₂, 4₂, 3₂, 2₂ будем иметь фронтальную проекцию линии пересечения гори­зонтально-проецирующей плоскости  и конуса.

Тогда точки М₂ и N₂ являются фронтальными проекциями точек пересе­чения прямой а и конуса, так как эти точки одновре­менно принадлежат пря­мой а и линии 1432, лежа­щей на поверхности кону­са. Далее по линиям связи получаем М₁ и N₁, принадлежащие a₁.

Видимость прямой a на П₁ и П₂ определяем исходя из видимости точек М и N. Так как М₁ и N₁ видимые, то невидимым будет лишь участок М₁N₁. Так же на П₂ невидимым является участок M₂N₂.

Касательные линии и плоскости к поверхности.

Линия является касательной к поверхности, если она имеет с ней одну общую точку и является касательной к любой кривой ли­нии, лежащей на этой поверхности. Такая точка называется точкой касания. Через одну точку на поверхности можно провести бесчисленное множество прямых, касательные к ней. При этом все касательные линии, проведенные к поверхности в данной точке, лежат в одной плоскости, которая называется касательной плоскостью.

Касательная плоскость является геометрическим местом всех ка­сательных, проведенных к данной кривой поверхности, проходящих через одну ее точку.

В

Рис. 1. 86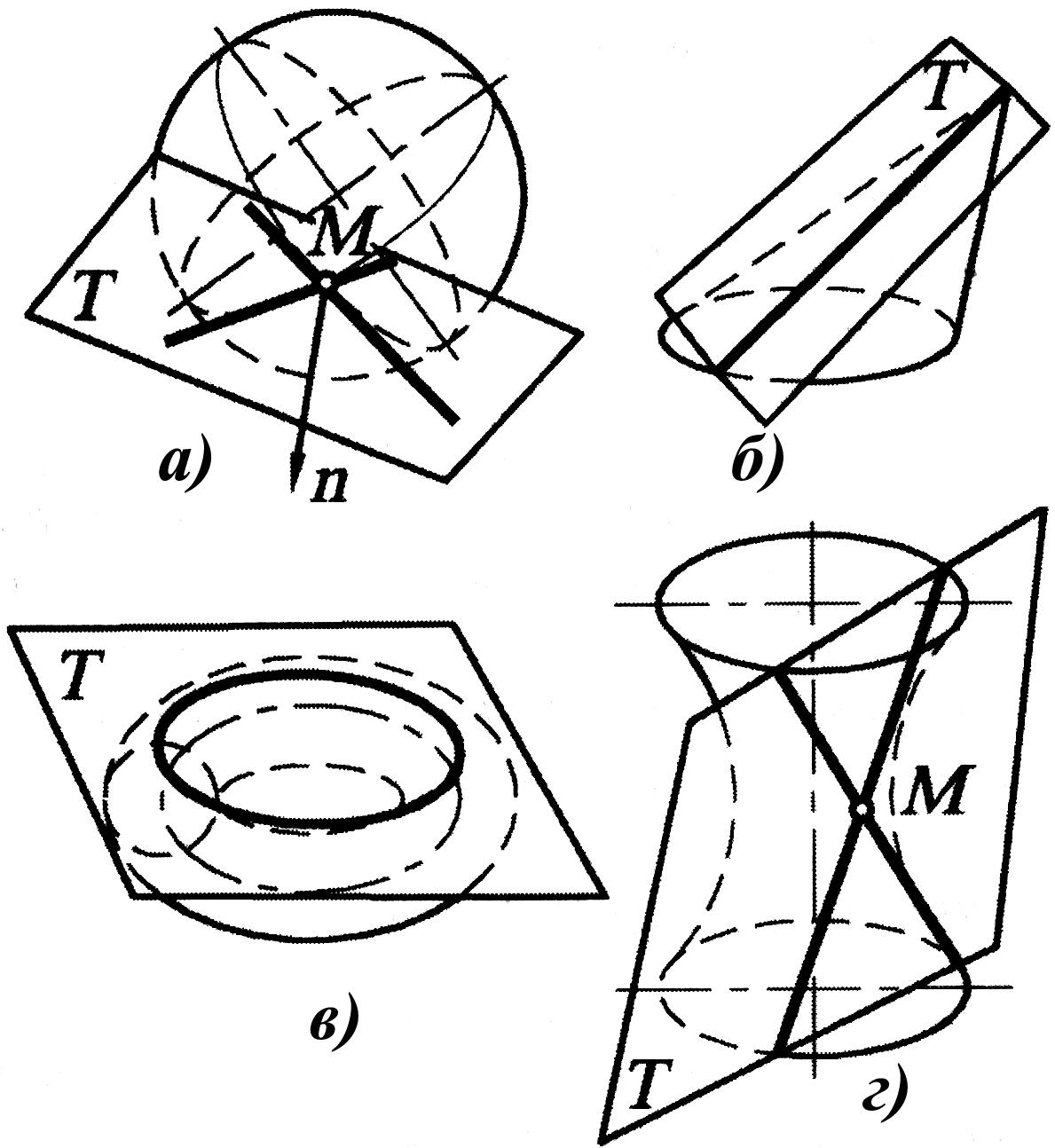

обыкновенной точке поверхности может быть построена только одна определенная касательная плоскость. В особых точках она или не определена, или не единственная, например: вершина коничес­кой поверхности; любая точка ребра возврата у торса и т.п.

Прямая п, проходящая через данную точку поверхности М пер­пендикулярно к касательной плоскости Т, называется нормалью по­верхности. (Рис. 1.86, а)

Для построения касательной плоскости в данной точке достаточно провести через эту точку две прямые, каждая из которых касается линий поверхности.

Если известна нормаль в данной точке, то два перпендикуляра к ней определяют касательную плоскость.

Существуют три случая взаимного расположения поверхности и касательной к ней плоскости:

- касательная плоскость и поверхность имеют единственную точку - точку касания (рис. 1.86, а);

- плоскость касается поверхности по линии t - прямой или кри­вой (рис. 1.86, б, в);

- плоскость, касаясь поверхности в единственной точке М, пере­секает ее по кривой линии (тор) или по двум прямым (однополостный гиперболоид вращения) (рис. 1.86, г).

Пересечение поверхности вращения плоскостью. В зависимости от положения секущей плоскости линия пересе­чения с поверхностью вращения имеет разную форму

Цилиндр. Если секущая плоскость параллельна осно­ванию, то линией пересечения с прямым цилиндром является ок­ружность. Если плоскость расположена под углом к основанию, тогда – эллипс. В случае, когда секущая плоскость перпендикулярна основанию, линия пересечения – прямоугольник.

Сфера. Линией пересечения плоскости со сферой является ок­ружность, независимо от положения секущей плоскости.

Тор. Если секущая плоскость перпендикулярна оси тора, то в сечении получаем кольцо (в частном случае круг). Когда секущая плоскость расположена под иным углом к оси тора, линия пересече­ния представляет собой пару окружностей, эллипсов, один эллипс, либо по форме похожа на цифру «8».

Конус. Наибольшее многообразие представляют кони­ческие сечения. Когда секущая плоскость конуса:

- параллельна основанию конуса, тогда линия пересечения — окружность;

- пересекает две образующих конуса, тогда линия пересе­чения – эллипс;

- параллельна образующей, тогда линия пересечения - парабо­ла;

- пересекает одну образующую, тогда линия пересечения — ги­пербола;

-

Рис. 1. 87

проходит через вершину конуса, тогда в сечении имеем треу­гольник.

Рассмотрим построение проекций на примере сечения прямого конуса, различно расположенными вышеназванными плоскостями, которые отсекают часть конуса. Как видим, на рис. 1.87 представле­но все многообразие расположения секущих плоскостей, которые являются фронтально-проецирующими.

Построим горизонтальную проекцию конуса, усеченного заданными плоскостями.

Линия пересечения представляет собой на участках S1 - отре­зок прямой, 12 - дугу окружности, 23 - участок параболы, 34 - уча­сток эллипса, 45 – гиперболу.

Для решения задачи достаточно построить горизонтальные про­екции точек 1, 2, 3, 4, 5, расположенных на поверхности конуса, и соединить их линией. Например, проекция 1₁ строится следующим образом: через точку 1₂ проводим горизонтальную прямую до пересечения с конту­ром конуса в точке 6₂, затем радиусом S₁6₁ проводим дугу окружно­сти и на ней по линии связи с точкой 1₂ находим точку 1₁. Аналогич­но строится горизонтальная проекция любой точки на поверхности конуса. Выбирая по мере необходимости промежуточные точки, получа­ем окончательное решение.

Профильную проекцию можно построить на основании правила взаимосвязи проекций. При этом необходимо учитывать контурные точки 7, 8, профильные проекции которых лежат на контуре S₃A₃. Поскольку участок образующей SA между точками 7 и 8 «вырезан» секущими плоскостями, как видно на П₂, то и на П₃ он отсутствует между точками 7₃, и 8₃.

Относительно осей Ф₁ и Ф₃ получаем симметричную картину, поэтому достаточно построить проекции на половине конуса. На чертеже (см. рис. 1.87, а) указываем линии пересечения секу­щих плоскостей, невидимые проекции которых обозначены пунк­тирной прямой.

Натуральная величина сечения. В качестве примера рассмотрим натуральную величину сечения ко­нуса плоскостью на участке 23. Для этого используем способ замены плоскостей проекций.

Ввиду того, что пространство чертежа не позволяет построить новую ось X₂₄ параллельно прямой 2₂3₂, начертим ее отдельно (см. рис. 1.87, б). Отметим точки 2, 9, 3, расстояние между которы­ми равно расстоянию между точками 2₂, 9₂, 3₂. Из каждой точки про­ведем перпендикуляр к оси, на котором откладываем расстояние от горизонтальных проекций 2₁, 9₁, 3₁ любой из точек до оси Ф₁, кото­рая выполняет роль оси П₂/П₁. Получаем точки 2₄, 9₄, 3₄ соединив которые кривой линией, построим натуральную величину сечения. На чертеже (см. рис. 1.87, б) сечение заштриховано наклонными прямыми.

Аналогично можно получить натуральную величину любого се­чения. Очевидно, что натуральную величину сечения горизонталь­ной плоскостью имеем без дополнительных построений на П₁, а вер­тикальной плоскостью - на П₃.

Пересечение поверхностей вращения.

Пересечение поверхности вращения многогранником. При пересечении поверхности вращения многогранником их общим геометрическим элементом является некоторая линия.

Рассмотрим построение этой линии на примере решения зада­чи о пересечении прямой трехгранной призмы и сферы. (Рис. 1.88)

П

Рис. 1. 88

оскольку боковые грани призмы перпендикулярны к П₁ то го­ризонтальная проекция линии пересечения призмы и сферы совпа­дает с горизонтальной проекцией призмы.

Остается построить фронтальную проекцию линии пересечения. Так как по двум проекциям геометрического объекта легко постро­ить третью, то здесь мы ограничимся построением горизонтальной и фронтальной проекций.

Применим метод вспомогательных секущих плоскостей, в каче­стве которых выберем фронтальные плоскости уровня, проходящие через характерные 1, 3, 5 и промежуточные 2, 4 точки, лежащие на линии пересечения призмы и сферы. Их горизонтальные проекции 1₁, 2₁, 3₁, 4₁, 5₁ показаны на рис. 1.88.

Линией пересечения фронтальной плоскости уровня со сферой является окружность, для построения которой на П₂ достаточно из­мерить расстояние от вертикальной оси до контура сферы на П₁, а затем этим радиусом на П₂ провести окружность.

Рассмотрим построение фронтальной проекции какой-либо точ­ки, например, точки 2. Проводим через нее фронтальную плоскость Ф*. Затем измеряем расстояние от точки 6₁ до 7₁, и этим радиусом проводим дугу окружности из точки О₂. Искомая точка лежит на пересечении этой дуги с линией связи, проведенной из точки 2₁.

Аналогично строятся точки 1₂, 4₂, 5₂. Через точку 3 нет необходимо­сти проводить вспомогательную секущую плоскость, так как она лежит на контуре сферы в проекции на П₂, и для построения точки 3₂ достаточно провести из точки 3₁ линию связи до пересечения ее с контуром сферы. Соединив точки 1₂, 2₂, 3₂, 4₂, 5₂, получаем один из участков искомой линии.

Так как участок линии между точками 5 и 8 лежит на фронталь­ной плоскости Ф***, что видно по его горизонтальной проекции 5₁8₁, то между точками 5₂ и 8₂ линия пересечения призмы и сферы пред­ставляет собой дугу окружности, проведенной через точку 5₂.

В связи с тем, что рассматриваемые поверхности симметричны относительно горизонтальной и профильной плоскостей уровня, искомая линия пересечения в проекции на П₂ симметрична относи­тельно вертикальной и горизонтальной осей, и ее построение не вызывает дополнительных трудностей.

Видимость линий определяется по видимости точек так же, как в предыдущих построениях.

Используя метод вспомогательных секущих плоскостей, можно построить линию пересечения любых поверхностей вращения и мно­гогранников. Если при построении линий пересечения вспомогатель­ных секущих плоскостей и рассматриваемых поверхностей возни­кают затруднения, тогда необходимо способом замены плоскостей проекций получить проекции указанных поверхностей в более удоб­ном виде.

Н

Рис. 1. 89

екоторые особые случаи пересечения поверхностей. В некоторых случаях расположение, форма или соотноше­ния размеров криволинейных поверхностей таковы, что для изображения линии их пересечения никаких сложных построе­ний не требуется. К ним относятся пересечения цилиндров с параллельными образующими, конусов с общей вершиной, соосных поверхностей вращения, поверхностей вращения, описанных вокруг одной сферы.

Изображения пересечения цилиндров с параллельными об­разующими приведены на рис. 1.89, а, конусов с об­щей вершиной — на рис. 1.89, б.

С

Рис. 1. 90

оосные поверхности вращения. Изображения пересечений соосно расположенных различных поверхностей вращения при­ведены на рис. 1.90. Конус, пересекающийся с двумя цилин­драми разного диаметра (рис. 1.90, а), часто используют при конструировании как переход от одного диаметра к другому.

Конус, сопряженный со сферой, с переходом на цилиндры (рис. 1.90, б), широко используют в качестве деталей меха­низмов управления — рукояток.

Комбинацию из трех соосных пересекающихся конусов (рис. 1.90, в) применяют при конструировании деталей, на­зываемых штифтами или роликами. Крайние конические по­верхности, называемые фасками, служат для упрочения кромки детали и предохранения тем самым от забоин основной рабо­чей конической поверхности. Комбинация из пересекающих­ся трех соосных конусов образует центровое гнездо для обработки деталей в центрах. Для предохранения от повреждений рабо­чей конической поверхности 1 при соприкосновении (ударах) с другими деталями служит наружный конус 2.

П

Рис. 1. 91

ересечение поверхностей, описанных вокруг одной сферы. Примеры изображения линии пересечения поверх­ностей вращения, описанных вокруг одной сферы, рассмотре­ны на рис. 1.91.

В случаях, показанных на рис. 1.91, а, б, поверхности двух цилиндров, конуса и цилиндра пересекаются по двум эллип­сам с проекциями 1₂2₂ и 3₂4₂.

В случае, показанном на рис. 1.91, в, пересечения кону­сов с вершинами S₂* и S₂, у которых имеются две параллельные образующие, линии пересечения — эллипс с проекцией 1₂2₂ и парабола с вершиной в точке с проекцией 3₂.

Рассмотренные примеры пересечения двух поверхностей вращения, описанных вокруг одной сферы, являются частны­ми случаями, следующими из теоремы Монжа.

Теорема Монжа. Если две поверхности второго порядка описаны около третьей поверхности (или вписаны в нее), то линия их пересечения распадается на две плоские кривые второго порядка (эллипс, гиперболу, параболу). Причем, плоскости этих кривых проходят че­рез прямую, соединяющую точки пересечения линии касания.

Р

Рис. 1. 92

ассмотрим решение задачи о нахождении линии пересечения конуса и цилиндра, изображенных на рис. 1.92, применяя теорему Монжа, что значительно упрощается такое решение.

Как видим, обе рассматриваемые поверхности описаны вокруг сферы. Построим решение сначала на П₂. Очевидно, точки 1₂, 2₂, 3₂, 4₂ являются точками пересечения конуса и цилиндра, так как лежат на контурных образующих. Тогда в соответствии с теоремой Монжа решением являются две прямые, проходящие через точки 1₂ и 3₂ и точки 2₂ и 4₂, т. к. эти прямые представляют собой фронтальные проекции плоскостей, согласно теореме.

В данном случае полученные линии пересечения цилиндра и конуса являются эллипсами, построение которых на П₁ ничем не отличается or построения любой линии, лежащей на поверхности конуса. Выбирая точки на фронтальной проекции каждой из линий 13 и 24, получаем их горизонтальные проекции.

Точки I, 2, 3, 4 лежат на образующей конуса, параллельной П₂, поэтому их положение на П₁ можно найти по линии связи, проходя­щей через 1₂, 2₂, 3₂, 4₂. Точки 5 и 6 выбраны на образующей цилин­дра, также параллельной П₂, что позволяет по фронтальным проек­циям 5₂ и 6₂, найти горизонтальные проекции 5₁ и 6₁, соответственно, которые являются точками перехода видимой части горизонтальной проекции линий пересечения цилиндра в конуса в невидимую.

Точка 7 является точкой касания цилиндра и конуса. Ввиду сим­метрии относительно фронтальной плоскости уровня решение на П₁ симметрично относительно горизонтальной оси, а на П₂ види­мые участки линии пересечения совпадают с невидимыми.

Метод вспомогательных секущих плоскостей концентрических сфер.

Для построения линии пересечения поверхностей вращения, рас­положенных произвольно в пространстве, удобно использовать уни­версальный метод вспомогательных секущих плоскостей.

Пересечение поверхностей, когда одна из них проецирую­щая. Если одна из пересекающихся поверхнос­тей проецирующая, то задача построения линии пересечения двух поверхностей упрощается и сводится к построению недо­стающих проекций кривой линии на одной из поверхностей по одной заданной проекции линии. На рис. 1.93 горизонтальная проекция линии пересечения прямого кругового цилиндра и с поверхностью сферы совпадает с горизонтальной про­екцией цилиндра. Ось вращения сферы и цилиндра пер­пендикулярны плоскости П₁.

Н

Рис. 1. 93

айдем сначала точки пересечения контурных образующих цилиндра с поверхностью сферы. (Рис. 1.93, а) Для этого проведем вспомогательные фронтальные плоскости так, чтобы плоскость ² прошла через фронтальные контурные образую­щие цилиндра, а плоскости ¹ и ³ — через профильные контурные образующие. Эти плоскости в то же время пересекут сферу по окруж­ностям, параллельным фронтальному меридиану (дугам R¹, R² и R³). Точки пересечения окружностей (дуг) с прямыми фронтальными проекциями образующих явятся фронтальными проекциями А ₂, В₂, С₂ и D₂ точек линии пере­сечения.

Горизонтальные проекции 1₁, 3₁, 5₁ и 7₁ этих точек будут находиться в точках пере­сечения прямых - проекций вспомогательных плоскостей с окружностью - проекцией бо­ковой поверхности цилиндра. Эти точки при­нято называть характерными.

Для нахождения проекций еще двух харак­терных точек 4 и 8 проводят через оси враще­ния сферы и цилиндра горизонтально-проеци­рующую плоскость δ (рис. 1.93, б); горизонталь­ные проекции 4₁ и 8₁ искомых точек находятся в точках пересечения прямой - проекции δ₁ - с окружностью - горизонтальной проекцией бо­ковой поверхности цилиндра - и не требуют дополнительных построений.

Фронтальные проекции этих точек опреде­ляются при помощи дополнительных фронталь­ных плоскостей ⁴ и ⁵, горизонтальные про­екции которых проводят через горизонтальные проекции 4₁ и 8₁ точек 4 и 8. Эти дополни­тельные фронтальные плоскости пересекают сферу по окружностям (дугам R⁴ и R⁵), a цилиндр по прямым - образующим; точки пе­ресечения дуг с прямыми явятся фронталь­ными проекциями 4₂ и 8₂ характерных точек; точку 4 называют высшей точкой, а точку 8 - низшей.

Проекции 2₁ и 6₁, 2₂ и 6₂ промежуточных точек определяются попутно с высшей и низ­шей точками.

Фронтальные проекции всех точек соединяют плавной кривой, получают искомую проекцию линии пересечения. Фронтальные проекции контурных образую­щих являются границами между видимой частью линии пересечения и невидимой. (Рис. 1.93, в)

Горизонтальная проекция этой линии сли­вается с горизонтальной проекцией основания цилиндра.

Р

Рис. 1. 94

ешим задачу о пересечении поверхностей прямого усеченного конуса и сферы. (Рис. 1.94)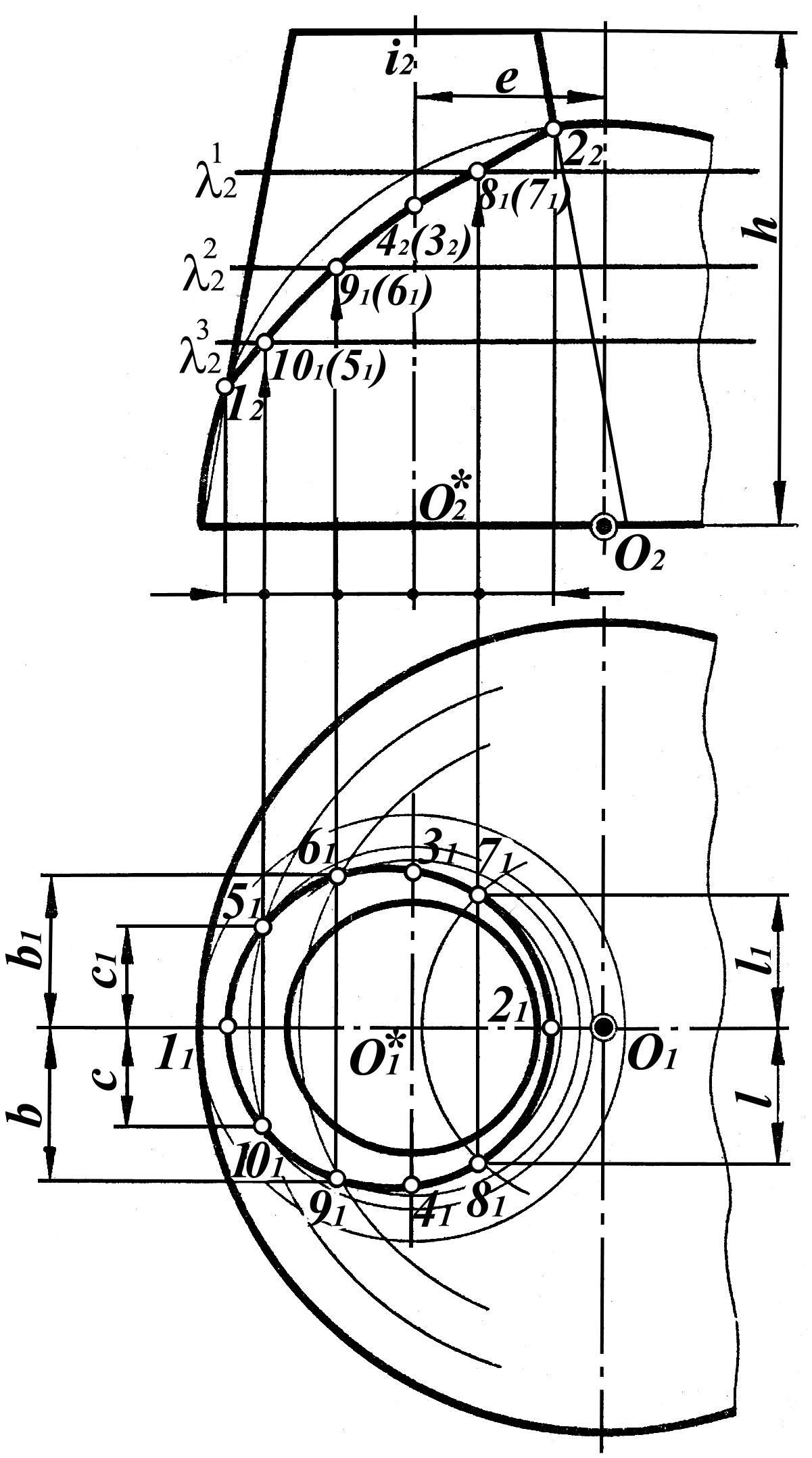

Ось сферы и ось вращения конуса перпендикулярны плоскости П₁. Фронтальные проекции характерных точек 1 и 2 определяются пересечением фронтальных проекций контурных образующих конуса с проекцией главного меридиана поверхности сферы.

Проекции промежуточных точек 3, 4, 5, 6, 7, 8, определяются при помощи ряда вспомогательных горизонтальных плоскостей λ¹λ²λ³. Эти плоскости пересекут каждое тело по соответствующей окружности - параллели, кото­рые, пересекаясь между собой, определят точки, одновременно принадлежащие поверхности сферы и поверхности конуса, а, следовательно, и линии пересечения.

Горизонтальные проекции параллелей ко­нуса проведены из точки О₁*, а сферы – из точки O₁.

Пересечения этих параллелей определяют горизонтальные проекции 3₁, 4₁, 5₁, 6₁, 7₁, 8₁ точек линии пересечения. Фронтальные проекции 3₂, 4₂, 5₂, 6₂, 7₂, 8₂ этих точек, найденные при помощи вертикальных линий связи, лежат на проекциях λ¹₂ λ²₂ λ³_2.

Найденные как горизонтальные, так и фрон­тальные проекции всех точек соединяют плав­ными кривыми и получают искомые проек­ции линии пересечения конуса и сферы. (Рис. 1.94).

Рассмотрим еще один пример, основанный на методе вспомогательных секущих концентрических сфер.

Этот метод применим лишь в случае выполне­ния трех условий:

- обе поверхности, линию пересечения которых мы определяем, являются поверхностями вращения;

- их оси должны пересекаться;

- оси этих поверхностей вращения должны быть параллельны одной из плоскостей проекций.

Как видим, для решения предыдущей задачи указанный метод не применим, т. к. не выполняется второе условие.

Р

Рис. 1. 95

ешим задачу о пересечении двух конусов, оси которых пересе­каются и параллельны П₂. (Рис. 1.95).

Центром концентрических сфер, которые обеспечивают допол­нительные построения, необходимые для решения задачи, является точка пересечения осей поверхностей вращения. В данном случае это точка О пересечения осей конусов.

Рассмотрим построение точек пересечения конусов с помощью произвольной сферы (см. рис. 1.95). Ее проекция на П₂ представляет собой окружность такого же радиуса, что и сфера.

Проекцией на П₂ линии пересечения построенной секущей сфе­ры с конусом является прямая, параллельная основанию конуса. Ее можно построить, соединив точки пересечения окружности и кон­тура конуса. Очевидно, что таких прямых две для каждого конуса.

Точки А₂, В₂, С₂ пересечения этих прямых между собой и явля­ются фронтальными проекциями точек пересечения конусов. Как видим, используя только одну окружность, можно получить несколь­ко точек пересечения конусов. Ясно, что их не может быть более четырех для одной дополнительно построенной сферы.

Далее строим горизонтальные проекции точек А, В, С, учиты­вая, что каждая из них является точкой на поверхности прямого конуса. Как излагалось ранее (см. построение конуса), для этого достаточно измерить расстояние от оси конуса до его контура по прямой, проходящей че­рез точку, горизонтальную проекцию которой строим. Затем этим радиусом из точки O₁ провести окружность и на ней по линии связи найти горизонтальную проекцию. На рис. 1.95 указанные построения выполнены для точки С₁ и С₁*, то понятно, что на П₂ имеем дело с двумя конкуриру­ющими точками. Поэтому, следует отметить, что построенная секущая сфера дает не три, а шесть точек пересечения конусов. Построение горизонтальных проекций осталь­ных точек ничем не отличается от вышеприведенного.

Для того, чтобы построить линию пересечения конусов, точек, через которые она проходит, должно быть, достаточное их количество. Дальнейшее решение данной задачи рассмотрим на рис. 1.96. Четыре точки 1₂, 2₂, 3₂, 4₂ имеем без дополнительных построений, так как они лежат на пересечении образующих конусов. Остальные точки на П₂ получим, проведя четыре окружности. Для окружности радиуса и, фронтальными проекциями точек пересечения конусов являются 5₂, 5₂*, 5₂**, 5₂***. Для окружности радиуса R₂ таких точек две - 6₂, 6₂*. Окружность радиуса R₃ дает также две точки - 7₂, 7₂*. Окружность радиуса R₄ позволяет п

Рис. 1. 96

олучить лишь одну точку 8₂. Очевидно, что проводить окружности радиусом, большим чем О₂4₂, и меньшим, чем R₂, не имеет смысла, так как не получим ни одной точки пересечения.

Как видно (см. рис. 1.96), четырех окружностей достаточно для того, чтобы построить фронтальную проекцию линии пересечения конусов, соединив найденные точки.

Для построения горизонтальной проекции полученных точек не­обходимо решить рассмотренную ранее задачу построения точек на поверхности конуса. Так, для построения точки, например, 7₁ надо измерить расстояние по горизонтальной линии, проходящей через 7₂, от оси до контура конуса, а затем этим радиусом из точки О₁ про­вести дугу. Точка 7₁ лежит на пересечении этой дуги с линией связи, проведенной из 7₂. Аналогично строятся горизонтальные проекции остальных точек.

Поскольку точки 5* и 5** лежат на образующей горизонтального конуса, которая на П₁ является контурной, то очевидно, что точки 5₁ * и 5₁ ** служат точками перехода линии пересечения конусов из види­мой зоны в невидимую.

С учетом того, что изображенные поверхности симметричны относительно фронтальной плоскости уровня, соединив построен­ные точки кривой линией, получим решение в окончательном виде (см. рис. 1.96).

В частном случае, когда размеры пересекающихся поверхностей вращения таковы, что обе они могут быть описаны вокруг одной и той же сферы, применима теорема Монжа.

Метод эксцентрических сфер. Этот метод можно применять для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии; каждая из этих поверхностей должна содержать семейство окружностей, по которым ее могут пересекать эксцентрические сферы, общие для обеих поверхностей.

Р

Рис. 1.97

ассмотрим пример основанный на этом способе. Построить линию пересечения поверхности тора с конической поверхностью вращения, имеющих общую фронтальную плос­кость симметрии. (Рис. 1.97)

Отмечаем точки видимости А и В в пересече­нии контура поверхности тора с контуром ко­нической поверхности. Для построения случай­ных точек здесь нельзя воспользоваться спосо­бом концентрических сфер, так как, хотя обе поверхности и являются поверхностями вра­щения, но их оси i¹ и i² не пересекаются. Спосо­бом же эксцентрических сфер, центры которых находятся в различных точках оси i² кониче­ской поверхности, можно найти сколько угодно случайных точек линии пересечения.

Действительно, у поверхности тора, кроме семейства окружностей (параллелей), располо­женных в плоскостях, перпендикулярных оси i¹, имеется семейство окружностей (меридианов), расположенных в плоскостях, проходящих че­рез ось i¹. Центры сфер, пересекающих поверх­ность тора по этим окружностям, будут нахо­диться на перпендикулярах к плоскостям этих окружностей, проведенных через их центры С¹, С², С³, ... Поэтому если взять центры эксцент­рических сфер в точках О¹, О², О³, ... пересечения этих перпендикуляров с осью i² кониче­ской поверхности, то сферы соответствующих радиусов пересекут обе данные поверхности по окружностям. Точки пересечения окружностей обеих поверхностей, принадлежащих одной и той же сфере, и будут точками искомой линии пересечения.

На рис. 1.97 проведены три эксцентрические сферы из центров О¹, О² и О³, с помощью кото­рых найдены случайные точки линии пересе­чения. Так, для построения точек М и N прове­ден меридиан 3—4 поверхности тора, распо­ложенный во фронтально проецирующей плос­кости, проходящей через ось i¹ (i₂¹), и из его центра С¹ (С₂¹) восстановлен перпендикуляр к этой плоскости. В точке О¹ (O₂¹) пересечения перпендикуляра с осью i² (i₂²) и будет нахо­диться центр вспомогательной сферы. Если теперь провести сферу с центром в точке О¹ (О₂¹) такого радиуса R, чтобы ей принадлежала ок­ружность 3—4, то эта сфера, пересекая кониче­скую поверхность по некоторой окружности 1—2, определит в пересечении окружностей 1—2 и 3—4 искомые точки М и N.

Горизонтальные проекции точек пересечения можно найти с помощью графически простых линий поверхности тора, которыми являются ее параллели. Так, горизонтальные проекции M₁ и N₁ точек М и N построены при помощи парал­лелей f¹ и f² поверхности тора. Точки видимо­сти Р и Q конической поверхности для плоско­сти П₁ построены приближенно, их фронталь­ные проекции найдены в пересечении фронталь­ных проекций линии пересечения и оси i² конуса.