1.6. Многогранники.

Многогранниками называются пространственные фигуры, состо­ящие из отдельных плоскостей (граней). Линии пересечения граней называются ребрами, которые представляют собой прямые линии.

Образование любой поверхности можно представить как непре­рывный ряд изображений, полученный при движении одной линии (образующей) по другой линии (направляющей). Поскольку и об­разующей, и направляющей может быть произвольная кривая ли­ния, то и поверхность может иметь любую произвольную форму, в общем случае достаточно сложную.

В

Рис. 1.61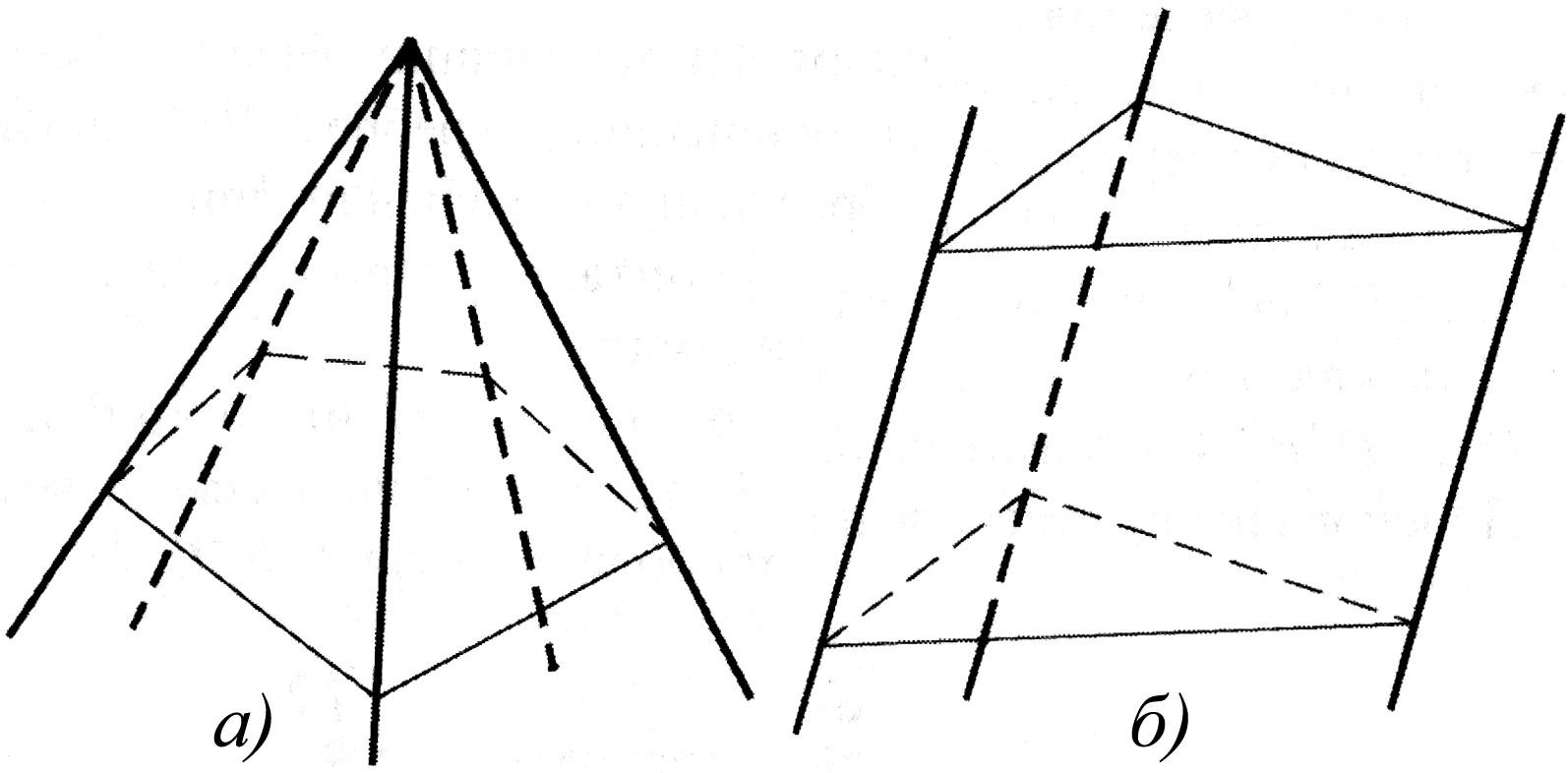

том случае, когда образующая и направляющая являются пря­мыми линиями, получаем простейшую поверхность - плоскость. Если образующей является прямая линия, а направляющей ломаная, получаем гранную поверхность. Когда образующая закреплена в од­ной точке, при движении по направляющей она вычерчивает пирамидальную поверхность (рис. 1.61, а). Если образующая перемеща­ется параллельно какому-либо направлению, получаем призмати­ческую поверхность (рис. 1.61, б).

Соответственно ограничив призматическую поверхность двумя параллельными между собой плоскостями, пересекающими образующие, получаем призму. Ограничив пирамидальную поверхность одной плоскостью, получаем пирамиду. Тогда эти секущие плоскости называются ос­нованиями многогранника, а образующие поверхности боковыми поверхностями.

Построение любых проекций точек на поверхности многогран­ника осуществляется наиболее эффективно при помощи образую­щих и направляющих, хотя можно использовать и другие приемы.

Как правило, задача формулируется следующим образом: по двум проекциям многогранника построить третью и начертить недостаю­щие проекции точки или линии на его поверхности.

Рассмотрим несколько примеров.

1

Рис. 1.62

. Пусть заданы фронтальная и горизонтальная проекции на­клонной призмы. Требуется построить отсутствующие проекции точек на ее поверхности, если на чертеже (рис. 1.62) есть точки 1₂, (2₁), (3₁), 4₁, (5₂).

Построим последовательно отсутствующие проекции точек.

Так как точка 1₂ лежит на ребре Е₂Е₂*, то 1₁ - на ребре Е₁*Е₁, что позволяет получить ее по линии связи. Поскольку ребро Е₁Е₁* неви­димое, то и (1₁) - невидимая.

Точка (2₁) - невидимая, значит, она принадлежит грани Е₁*Е₁D₁D₁*. Проводим через нее образующую, параллельную любому боковому ребру до пересечения с основанием. Затем по линии связи получаем фронтальную проекцию точки на основании (на ребре Е₂* D₂*), после чего проводим через эту точку образующую и на ней по линии связи от (2₁) находим 2₂. Поскольку на фронтальной проекции грань Е₂*Е₂D₂D₂* видимая, то и точка 2₂ видимая

Так как точка 3₁ невидимая то она лежит на основании A₁*B₁*C₁*Е₁*D₁*. Следовательно точка 3₂ строится по линии связи ведь на П₂ основание призмы представляет собой прямую A₂*B₂*C₂*Е₂*D₂*.

Используя описанный принцип можно построить остальные проекции (4₂), 5₁.

2. Пусть заданы фронтальная и горизонтальная проекции пирамиды SABC и проекции точек 1₂, 2_2, 3₂. Надо построить третью проекцию пирамиды и отсутствующие горизонтальные и профильные проекции точек 1, 2, 3. (Рис.1.63)

Д

Рис. 1.63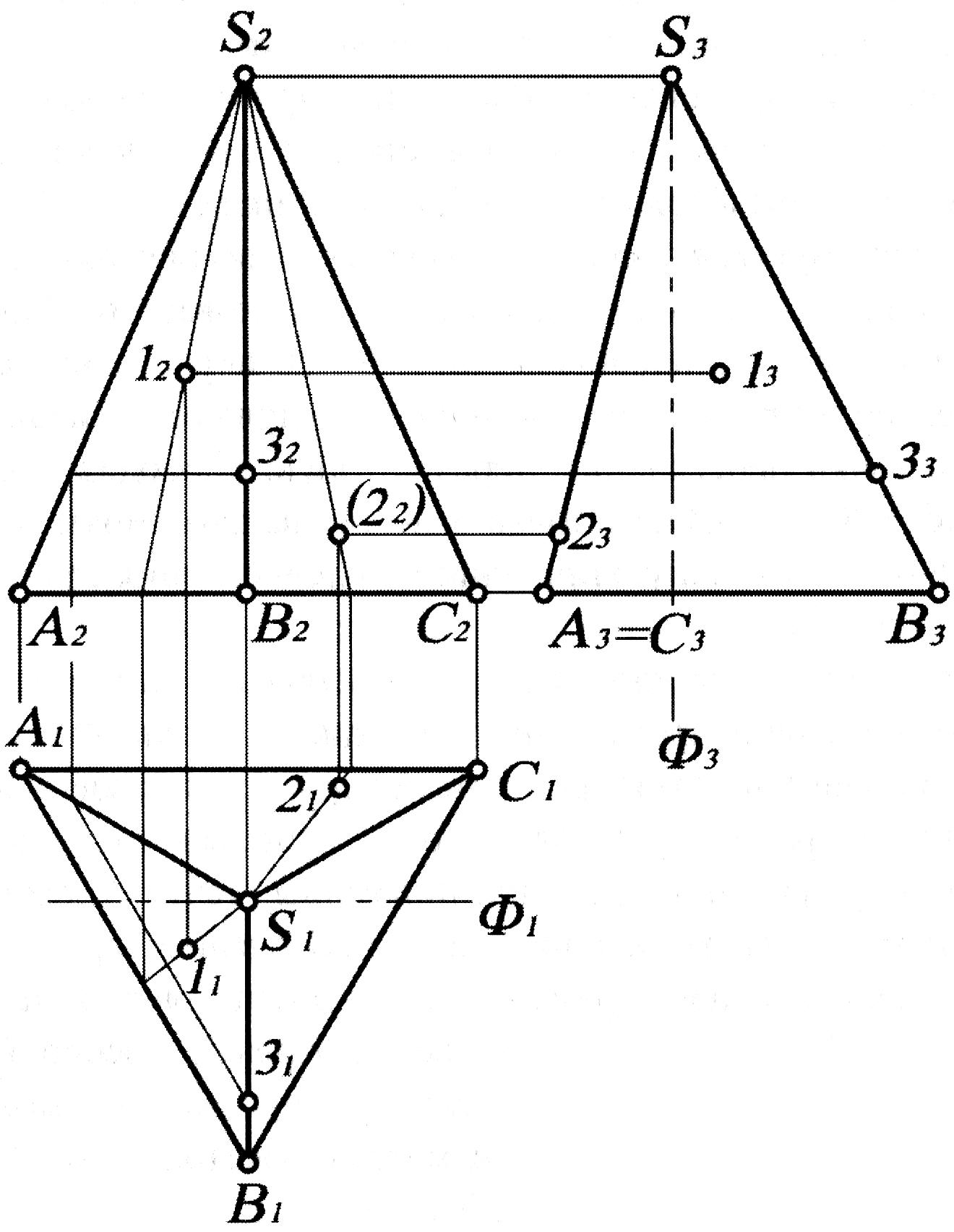

ля построения профильной проекции пирамиды через верши­ну S проведем фронтальную плоскость уровня. Тогда ее горизон­тальная Ф₁ и профильная Ф₃ проекции будут служить базовыми линиями взамен традиционных осей проекции ОХ и OZ. Точку S₃ по­лучаем по линиям связи на базовой линии. Затем определяем положение точек А₃= С₃ и B₃ откладывая от базовой линии Ф₃ от­резки равные расстояниям от A₁, С₁, В₁ до Ф₁ соответственно.

Соединив точки основания с вершиной, получаем профильную проек­цию пирамиды. Как видим, грань SAC на профильной плоскости проекций вырождается в S₃A₃ (или S₃C₃).

Решим вторую часть задачи - построение отсутствующих про­екций точек 1, 2, 3. Для определения положения горизонтальной про­екции 1₁ используем образующую пирамиды проведем через вер­шину S₂ и точку 1₂ прямую до пересечения с ребром A₂ В₂ основания. Затем по линии связи получим горизонтальную проекцию этой точ­ки на ребре А₁В₁. Соединив полученную точку с вершиной S₁ будем иметь горизонтальную проекцию образующей. На ней и лежит точ­ка 1₁ положение которой определим по линии связи с 1₂. Аналогич­но можно построить горизонтальную проекцию 2₁ с учетом того, что 2₂ – невидимая. Значит, точка 2 лежит на грани SAC. Тогда осно­вание образующей попадает на ребро АС основания. В остальном построения полностью повторяют предыдущие.

Однако для определения положения горизонтальной проекции 3₁ использовать образующую не представляется возможным, так как ребро SB, на котором лежит точка 3, в проекциях на П₁, П₂ дает вер­тикальную прямую (т. е. является профильной линией уровня). В этом случае используют линию, параллельную основанию. Через точку 3₂ проводят прямую, параллельную А₂В₂, до пересечения с ребром S₂A₂. Затем на ребре S₁A₁ по линии связи получают горизонтальную проекцию точки пересечения, через которую проводят прямую па­раллельно A₁В₁. Поскольку точка 3 лежит на этой прямой, то про­должая ее горизонтальную проекцию до пересечения с ребром S₁B₁ получаем точку 3₁.

Профильную проекцию 1₃ строим на основании взаимосвязи меж­ду горизонтальной и профильной проекциями точки. А именно, от­кладываем по линии связи, проходящей через 1₂, от базовой линии Ф₃ вправо отрезок, равный расстоянию от 1₁ до Ф₁ как это делалось при построении профильной проекции пирамиды. Точка 2₁ лежит на пе­ресечении горизонтальной линии связи, проходящей через 2₂, и грани S₃A₃C₃ превратившейся в прямую S₃A₃. Наконец, точку 3₃ находим на горизонтальной линии связи, проходящей через 3₂ и ребро S₃B₃.

Следует заметить, что горизонтальную проекцию 3₁ можно най­ти через профильную. Для этого измеряем расстояние от 3₃ до Ф₃ и откладываем его вниз от Ф₁ по ребру S₁B₁.

При использовании базовой линии (взамен осей проекций) не­обходимо учитывать направление, в котором строятся проекции.

Подчеркнем, что когда горизонтальная проекция какой-либо точки расположена ниже Ф₁ профильная проекция этой точки лежит вправо от Ф₃; если горизонтальная проекция выше Ф₁ тогда профильная левее Ф₁. Это очевидно, так как профильная проекция соответствует взгляду на любую точку (а следовательно, и любой геометрический объект) слева.

Л

Рис. 1.64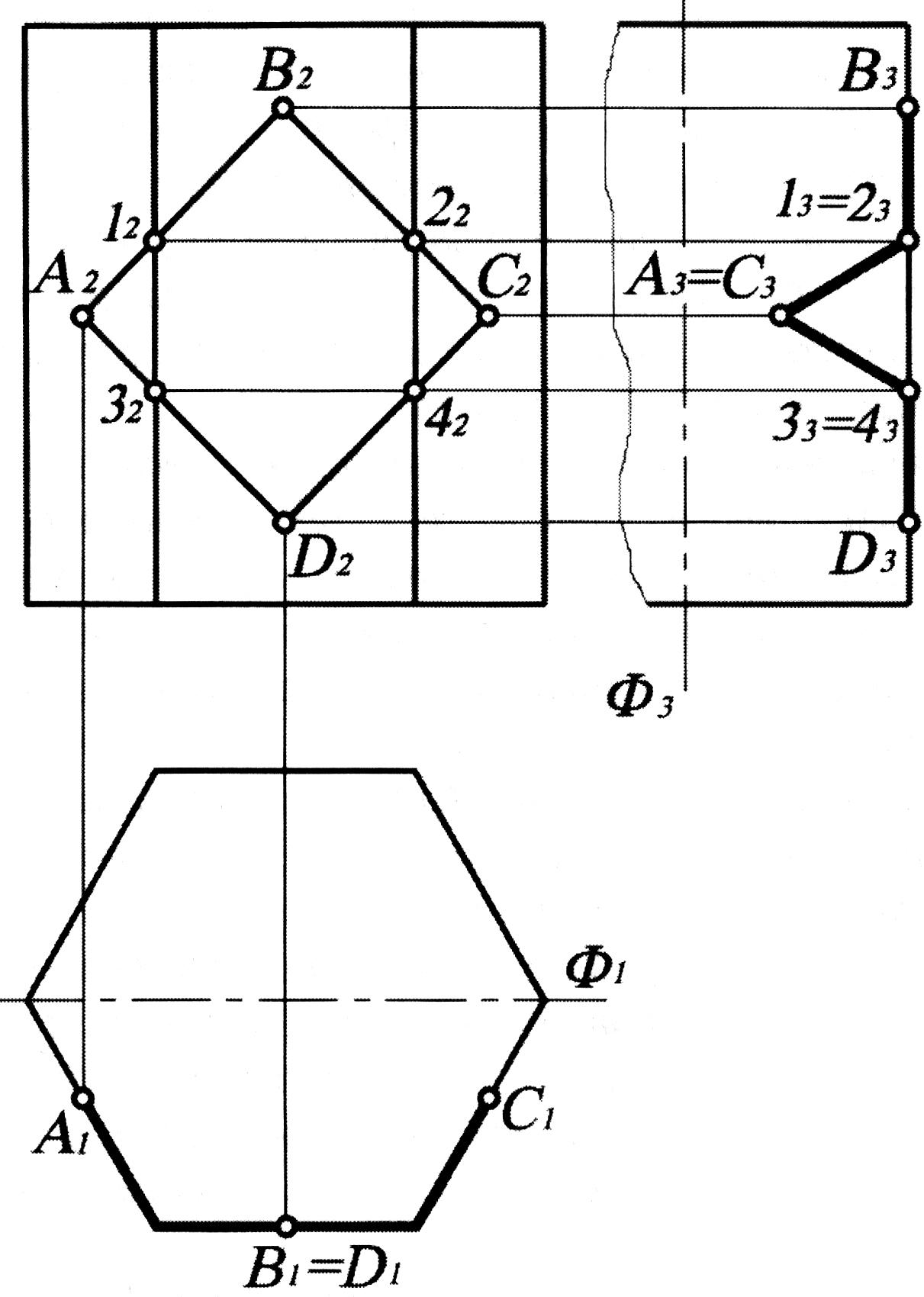

инию на поверхности многогранника можно построить по характерным точкам, которыми являются точки ее изгиба и точки перехода через ребра. При этом следует помнить, что лома­ная линия на поверхности многогранника будет ломаной, состоящей из отрезков прямой, в любой плоскости проекции, а кривая кривой (за исключением частных случаев).

3. По фронтальной проекции A₂B₂C₂D₂ ломаной линии лежащей на поверхности прямой шестигранной призмы (рис. 1.64) постро­ить горизонтальную и профильную проекции.

Поскольку призма прямая и ее боковые ребра являются горизон­тально-проецирующими линиями, то на П₁ проекция граней вырож­даются в отрезки прямой, составляющие ломаную линию (шести­угольник). Следовательно, горизонтальная проекция любой точки боковой поверхности призмы лежит на этом шестиугольнике, в том числе и точки линии A₁В₁С₁D₁.

Для построения профильной проекции A₃В₃С₃D₃ требуется най­ти промежуточные точки ломаной, лежащие на ребрах призмы. Эти точки 1, 2, 3, 4 являются характерными. По фронтальным проекци­ям 1₂, 2₂, 3₂, 4₂ найдем профильные проекции 1₃= 2₃, 3₃=4₃ исполь­зуя горизонтальные линии связи. Аналогично строим точки В₃, D₃. Они лежат на том же ребре, т. к. грань, являющаяся фронтальной ли­нией уровня, превращается на П₃ в прямую. Точки A₃С₃получаем, откладывая от Ф₃ вправо по линии связи с А₂, С₂ расстояние, отме­ренное A₁, С₁ до Ф₁. Соединяя полученные точки, имеем решение в виде замкнутой ломаной A₃1₃В₃2₃С₃D₃3₃ A₃.

Заметим, если линия на поверхности многогранника замкнутая, то и все ее проекции замкнутые линии.

4

Рис. 1.65

. По фронтальной проекции кривой линии лежащей на поверхности прямой пирамиды, построить горизонтальную и профильную. (Рис. 1.65)

Характерными точками для этой кривой будут точки 1₂, 2₂, 3₂, 4₂, лежащей на пересечении с ребрами S₂B₂, S₂С₂. Промежуточных то­чек можно выбрать любое количество (чем больше, тем точнее решение): 5₂, 6₂, 7₂, 9₂.

Горизонтальные и профильные проекции характерных точек 1₃ = 2₃ и 3₃ = 4₃ получим по линиям связи. Далее любую из промежу­точных точек построим, используя прямые, параллельные соответ­ствующим ребрам основания. Так для точки 7₂ эта прямая параллельна С₂D₂, следовательно, на П₁ она параллельна С₁D₁.

По горизонтальным и фронтальным проекциям, используя пра­вило взаимосвязи проекций, строятся профильные проекции. Соеди­нив проекции точек, получим замкнутую кривую 1₃9₃2₃8₃7₃3₃6₃4₃5₃1₃ невидимые участки которой совпадают с видимыми.

Таким образом, построение проекций любой, сколь угодно слож­ной кривой базируется на построении проекции точек, расположен­ных на этой кривой.

Пересечение многогранника прямой. Для определения точек пересечения прямой и многогранника, так же как в задаче о пересечении прямой и плоскости, необходимо через заданную прямую провести вспомогательную плоскость частного положения. Пусть требуется определить точки пересечения пря­мой а и призмы АВСА*В*С*. (Рис. 1.66)

П

Рис. 1.66

роведем через прямую а фронтально-проецирующую плос­кость , тогда =а₂. Определим фронтальные проекции точек пересечения плоскости  с призмой. Это точки 1, 2, 3, 4, где плоскость  пересекает ребра призмы. Их фронтальные проекции 1₂, 2₂, 3₂, 4₂ легко получить на линии а₂. Ясно, что по этим точкам про­ходит фронтальная проекция 1₂2₂3₂4₂ плоской фигуры, полученной в результате пересечения  и призмы. Для построения ее горизон­тальной проекции достаточно по линиям связи найти горизонталь­ные проекции точек 1₁, 2₁, 3₁, 4₁, лежащих на соответствующих ребрах призмы, соединив которые получим искомую плоскую фигуру 1₁2₁3₁4₁ . Стороны этого четырехугольника лежат на соответствую­щих гранях призмы.

Следовательно, зная видимость граней призмы можно определить видимость сторон четырехугольника на П₁: невидимой являет­ся лишь сторона 3₁4₁. Очевидно, что точки М₁ и N₁ - горизонтальные проекции точек пересечения прямой а и призмы, так как они одно­временно принадлежат и прямой а и линиям 23 и 34, лежащим на поверхности призмы. По линиям связи найдем положение точек М₂ и N₂, лежащих на а₂.

Видимость определяется по принадлежности точек М и N граням призмы. Так как точка М₁ лежит на видимой грани В₁С₁С₁*В₁*, то она видимая; точка N₁ принадлежит невидимой грани А₁А₁*В₁*В₁, следовательно, она невидимая. Однако после «выхода» из призмы в точке N₁ прямая a₁ не сразу становится видимой, т. к. она остает­ся закрытой гранями призмы. Аналогично определяем видимость точки М₂, принадлежащей видимой грани В₂С₂С₂*В₂*, и невидимость точки N₂, принадлеж

Рис. 1.67

ащей невидимой грани A₂A₂*В₂*В₂. Невидимые участки прямой а обозначим пунктирной линией.

Используя те же приемы, можно определить точки пересечения прямой b и пирамиды SABCD. Построения производим с помощью горизонтально-проецирующей плоскости проходящей через задан­ную прямую b. (Рис. 1.67)

Последовательность построений та же, что в предыдущей задаче так как b₁ = ₁, то находим все точки 1₁, 2₁, 3₁, 4₁ пересечения с ребра­ми, затем по ним - точки 1₂, 2₂, 3₂, 4₂, соединяем их и получаем четырехугольник 1₂2₂3₂4₂, далее определяем пересечение b ₂ со сторона­ми четырехугольника, т. е. точки М₂ и N₂ по ним на b ₁ находим М₁ и N_1. Видимость определяем исходя из вышеизложенных принципов.

Пересечение многогранника плоскостью. На рис. 1.68 показано пересечение пирамиды плоскостью общего положения α, выраженной следами. Все сводится к нахождению точек пересечения ребер SA, SB и SC с плоскостью α, т. е. к задаче на пересечение прямой с плоскостью. Рас­смотрим нахождение точки L, в которой ребро SB пересекает плоскость α. Выполним сле­дующие построения:

1

Рис. 1.68

) через SB проводим вспомогательную плоскость, в данном случае горизонтально-проецирующую β;

2) находим прямую пересечения 1—2 пло­скостей α и β;

3) находим точку L в пересечении прямых SB и 1—2.

Далее, так как в данном случае ребро SA расположено параллельно плоскости П₂, про­водим через него вспомогательную фронтальную плоскость . Она пересекает плоскость α по ее фронтали с начальной точкой 3; в пересечении этой фронтали с ребром SA получаем точку К.

Обратим внимание на особенность в данном примере: проек­ция A₁С₁ параллельна следу α₁. Это тот случай, когда у двух плоскостей горизон­тальные следы взаимно параллельны (α₁ A₁С₁, но A₁С₁ - часть горизонтального следа плоскости грани SAC) и линия пересечения таких плоскостей является их об­щей горизонталью. Поэтому мы можем провести через уже найденную точку К прямую, параллельную ребру АС (или || α₁), и так найти точку М.

Если бы не было этих особенностей, то следовало бы поступать аналогично построению точки

Чертеж на рис. 1.68 выполнен согласно условию, что плоскость α прозрачна и что основным является нанесение на гранях линий разделения пирамиды на две части.

Натуральная величина сечения. Задача о пересечении многогранника плоскостью решается по­строением вспомогательных секущих плоскостей. Пусть требуется найти общие геометрические элементы плоскости, заданной пере­секающимися прямыми b и d, и призмы ABCDA*B*C*D*. (Рис. 1.69)

О

Рис. 1.69

чевидно, что этими общими геометрическими элементами бу­дут отрезки прямой. Для упрощения построений вспомогательные секущие плоскости проведем через ребра призмы. В данном случае удобнее использовать горизонтально-проецирующие плоскости , *, **, ***. Тогда линиями их пересечения с плоскостью будут на П₁ прямые 5₁5₁*, 6₁6₁*, 7₁7₁* 8₁8₁*. По линиям связи найдем фронтальные проекции 5₂5₂*, 6₂6₂*, 7₂7₂*, 8₂8₂* линий пересечения секущих плоскостей с заданной плоскостью. Далее определим точки пересечения этих линий с соответствующими ребрами призмы: например, для ребра DD*, через которое проходит вспомогательная секущая плоскость  линией пересечения плоскости  и заданной плоскости будет 88*, а значит в проекции на П₂ точкой пересечения заданной плос­кости и ребра DD* является точка 1₂. Аналогично построим другие точки 2₂, 3₂, 4₂. Соединив их, получаем ломаную линию 1₂2₂3₂4₂, которая является фронтальной проекцией линии пересечения плоскости заданной пересекающимися прямыми b и d, и призмы. Горизонтальную проекцию ломаной линии 1₁2₁3₁4₁ легко построить по ли­ниям связи, опущенным на соответствующие проекции ребер призмы. Видимость участков проекции ломаной линии определяем по принадлежности граням призмы.

Сечение многогранника называется плоская фигура, расположенная в секущей плоскости и ограниченная линиями пересечения ее с многогранником. Очевидно, что такая фигура представляет собой некоторый многоугольник. Так, на рис. 1.70 это четырехугольник 1234.

Нередко практический интерес представляет задача определения натуральной величины сечения. Ранее был рассмотрен спо­соб замены плоскостей проекций, позволяющий решать подобные задачи.

О

Рис. 1.70

пределим натуральную величину сечения (четырехугольника), полученного на рис. 1.69. Так как четырехугольник 1234 занимает об­щее положение в пространстве, то его натуральную величину мож­но определить двумя переменами плоскостей проекций, сначала по­строив плоскость, перпендикулярную четырехугольнику 1234, а за­тем - параллельную ему. Чтобы рассмотреть его более подробно, вынесем построения на отдельный чертеж. (Рис. 1.70) Для построения плоскости, перпендикулярной плоскости четырехугольника 1234, не­обходимо начертить одну из главных линий, например, горизонталь. Ее фронтальная проекция h₂ должна быть параллельна оси X₁₂. По точкам пересечения 2 и 4 с четырехугольником 1234 находим и го­ризонтальную проекцию h₁ горизонтали.

Новая ось X₁₄ разделяющая П₁ и новую плоскость П₄, должна быть перпендикулярна h₁. Затем получаем проекцию 1₄2₄3₄4₄ в виде прямой.

И, наконец, вычертив вторую новую ось Х₅₄ параллельно 1₄3₄, построим проекцию 1₅2₅3₅4₅ четырехугольника в плоскости П₅. Это и есть натуральная величина четырехугольника 1234. Сечение ш­трихуем под углом 45° к горизонтальной прямой.

Чаще приходится решать более простую задачу - определение натуральной величины сечения многогранника плоскостью частно­го положения. В этом случае достаточно сделать всего одну замену плоскостей проекций. Рассмотрим на примере построение сечения пирамиды горизонтально-проецирующей плоскостью . (Рис.1.71) Пусть задана горизонтальная проекция ₁. Необходимо найти ли­нию пересечения плоскости  с пирамидой и определить натураль­ную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П₁ и П₂, а затем определить его натуральную величину.

Чтобы решить первую часть задачи, нужно найти все точки пе­ресечения плоскости  с ребрами пирамиды и соединить их отрез­ками прямой. Горизонтальная проекция ₁ пересекает ребра пира­миды в точках 1₁, 2₁, 3₁, 4₁. (Рис. 1.71, а) По линиям связи находим их фронтальные проекции 1₂, 2₂, 3₂, 4₂ на фронтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения 1₂, 2₂, 3₂, 4₂ заданной плоскости с пирамидой. Отрезок 1₂4₂ этой линии будет невидимым, так как он лежит на невидимой грани A₂S₂C₂. Плоская фигура, ограниченная полученной линией (на рис. 1.71, а заштрихованная область), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.

Д

Рис. 1.71

ля определения натуральной величины четырехугольника 1234 способом замены плоскостей проекций не обязательно строить но­вую ось параллельно ₁ (или 1₁, 2₁, 3₁, 4₁), ввиду ограниченности пло­щади чертежа. Достаточно соблюдать основные принципы построе­ния. Начертим новую ось на свободном поле чертежа. Перенесем на нее точки 1₁, 2₁, 3₁, 4₁ не меняя расстояния между ними. Проведем через них перпендикуляры к оси. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси X₁₂ , которую считаем расположенной на основании А₂В₂С₂ пирамиды, до соответ­ствующих проекций 1₂2₂3₂4₂. Соединив указанные точки, полу­чим натуральную величину сечения пирамиды заданной плоскостью . (Рис. 1.71, б)

Как видим, сечение в натуральную величину отличается от 1₂2₂3₂4₂ лишь тем, что оно вытянуто вдоль ₁ .

В

Рис. 1.72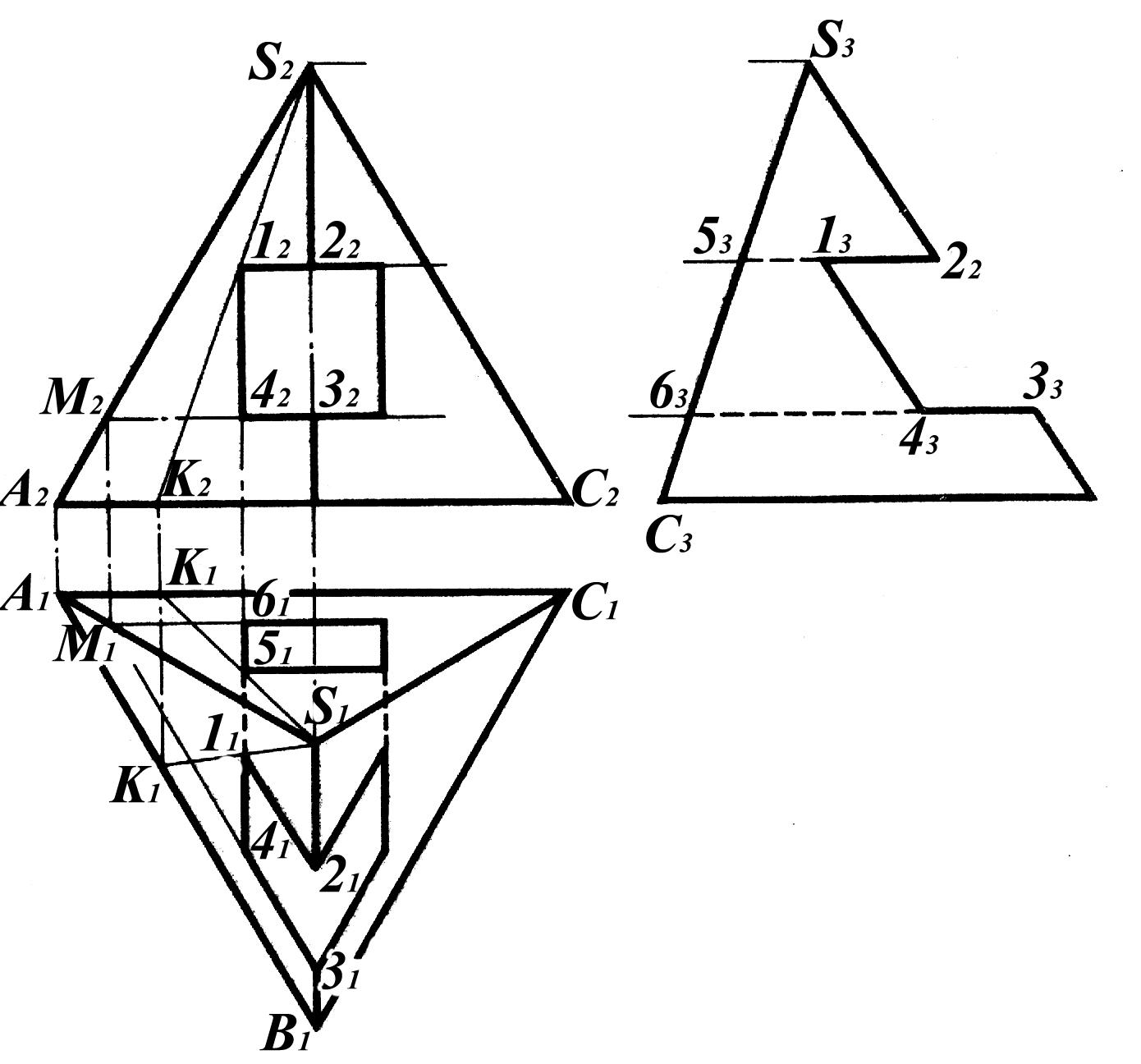

ырезы в многогранниках. На рис. 1.72 изображен многогранник в форме правильной треугольной пирамиды с призматическим отверстием в ней. Построе­ние проведено по фронтальной проекции, заданной полностью. На чертеже показано построение точек 1 и 5 (на горизонталь­ной проекции) при помощи прямых, про­веденных через вершину S. Точки 3, 4 и 6 (на горизонтальной проекции) найдены при помощи прямых, проходящих на гранях SAB и SAC параллельно плоскости П₁; гори­зонтальные проекции этих прямых про­ходят через точку М₁ параллельно А₁В₁ и А1С₁. Точка 2 может быть найдена в дан­ном случае либо аналогично точке 3, либо при помощи проекции на плоскость П₃.

Пересечение двух многогранников. При пересечении двух многогранников общим геометрическим элементом является замкнутая ломаная линия, состоящая из участ­ков прямой, так как многогранники образованы из плоскостей, а линия пересечения плоскостей представляет собой прямую. Точки излома получаются в местах пересечения граней одного многогран­ника с ребрами другого.

В том случае, когда один из многогранников занимает частное положение (т. е. его боковые грани проецируются на одну из плоско­стей проекций в многоугольник), задача построения линии их пере­сечения решается достаточно просто. Ввиду того, что одна из проекций многогранника - многоугольник, проекция линии пересече­ния на эту плоскость проекций совпадает с ним. Поскольку линия пересечения многогранников принадлежит каждому из них, то зада­ча сводится к построению отсутствующих проекций ломаной ли­нии, а, следовательно, к построению проекций точек на поверхнос­ти многогранника и соединению их отрезками прямой. Заметим, что частное положение может занимать лишь призма, так как только ее можно расположить таким образом, чтобы боковые ребра, а значит, и грани были перпендикулярны плоскости проекций.

Рассмотрим построения на следующем примере. Пусть пересекаются пирамида и призма частного положения. (Рис. 1.73) Требуется построить проекции линии их пересечения.

П

Рис. 1.73

оскольку призма расположена так, что все ее боковые грани перпендикулярны П₁, то на П₁ ее боковая поверхность проецируется в линию, точнее в треугольник D₁E₁F₁. И горизонтальной проекцией линии пересечения призмы DEFD*E*F* и пирамиды SABC является ломаная линия 1₁E₁5₁. Таким образом, горизонтальная проекция ли­нии пересечения призмы и пирамиды получена без каких бы то ни было дополнительных построений. Следует учитывать, что грани призмы пересекают не только грань SAC, но и грани SBC и SAB пи­рамиды, что очевидно из рассмотрения чертежа (см. рис. 1.73) на П₁. Следовательно, можно отметить все точки излома линии пересече­ния 1₁E₁5₁, расположенные на пересечении ее с ребрами пирамиды. А именно, точки 1₁, 2₁, 3₁, 4₁, 5₁, 6₁. Очевидно, что 3₁ = 6₁, так как ребро ЕЕ* призмы пересекает две грани SAB и SAC пирамиды.

Линия пересечения на каждой из проекций должна быть замкну­той. Причем ясно, что можно соединять отрезками прямой лишь точ­ки, лежащие на одной и той же грани. Эти правила универсальны и относятся к любой задаче о пересечении многогранников.

Тогда на П₁ получаем горизонтальную проекцию линии пересе­чения призмы и пирамиды в виде ломаной 1₁2₁3₁4₁5₁6₁1₁, лежащей на гранях пирамиды (вместе с тем и призмы).

Для нахождения фронтальной проекции этой линии необходимо решить задачу построения проекций ломаной линии на поверхнос­ти пирамиды. Достаточно построить фронтальные проекции указан­ных точек. Так как точки 1, 2, 4, 5 лежат на ребрах пирамиды, то их фронтальные проекции 1₂, 2₂, 3₂, 4₂, 5₂ легко получить по линиям связи. Для нахождения фронтальных проекций 3₂ и 6₂ точек 3 и 6, лежащих на гранях SAB и SAC соответственно, необходимо через точки 3₁ и 6₁ провести образующие S₁7₁ и S₁8₁. Точки 7 и 8 лежат на основании пирамиды, поэтому по линиям связи можно найти фронтальные про­екции 7₂ и 8₂ на соответствующих ребрах основания A₂С₂ и А₂В₂ пи­рамиды. Построив фронтальные проекции S₂7₂ и S₂8₂ образующих, по линиям связи отметим на них точки 3₂ и 6₂. Соединив точки, по­лучим замкнутую ломаную 1₂2₂3₂4₂5₂6₂1₂. Последовательность со­единения определяется по горизонтальной проекции на основании правила принадлежности соседних точек пересечения одной и той же грани. Например, ошибочным было бы соединение точек 1₂ и 3₂, так как одна из них лежит на ребре S₂С₂, а другая на грани S₂A₂B₂.

Видимость точек и линий на П₂ определяется по принадлежнос­ти граням пирамиды, так как обе грани D₂E₂E₂*D₂* и E₂F₂F₂*E₂* явля­ются видимыми. Поскольку грани S₂A₂С₂ и S₂B₂С₂ невидимые, то и точки, и прямые, лежащие на них, также невидимые. Проведя неви­димые линии пунктиром, получим решение в окончательном виде.

Рассмотрим теперь случай, когда оба многогранника занимают общее положение в пространстве. Решение задачи о нахождении линии их пересечения усложняется, поскольку нужно строить все проек­ции этой линии. Линия пересечения многогранников проходит че­рез точки пересечения ребер первого многогранника с гранями вто­рого и граней первого с ребрами второго.

Для решения применим метод секущих вспомогательных плос­костей, уже рассмотренный нами ранее. Чтобы получить какую-либо точку пересечения многогранников, необходимо найти линию пере­сечения вспомогательной плоскости с одним из них, затем с другим, далее - точку пересечения этих линий.

Рассмотрим на примере.

Пусть пересекаются четырехгранная пирамида SABCD и трехгранная призма EFGE*F*G*. (Рис. 1.74) Необходимо определить про­екции точек пересечения ребер призмы с гранями пирамиды ребер пирамиды с гранями призмы.

Ч

Рис. 1.74

ерез ребра призмы ЕЕ*, FF*, GG* проведем вспомогательные фронтальные плоскости уровня Ф, Ф*, Ф**. При выборе положения вспомогательной секущей плоскости в каждом конкретном случае руководствуемся правилом вспомогательная плоскость должна быть плоскостью частного положения и пересекать многогранники по линиям, проекции которых построить несложно. В данном случае линии пересечения с призмой плоскостей Ф, Ф*, Ф** проходят по ее ребрам, значит, ее проекции совпадают с проекциями ребер призмы.

Рассмотрим одну из вспомогательных плоскостей Ф. Ее гори­зонтальная проекция Ф₁ проходит по ребру G₁G₁*. Линия пересече­ния с пирамидой проходит через точку основания 1₁ и параллельна ребру S₁A₁. По линии связи находим фронтальную проекцию 1₂ и через нее проведем прямую, параллельную А₂ S₂, которая является фронтальной проекцией линии пересечения плоскости Ф и пирами­ды. Очевидно, что там, где эта линия пересекает ребро G₂G₂*, и ле­жит фронтальная проекция 7₂ точки пересечения ребра GG* и грани SAD пирамиды. По линии связи найдем 7₁. Аналогично строятся точ­ки 4₂, 5₂, а по ним 4₁, 5₁.

Теперь проведем вспомогательную плоскость Ф*** по ребру SA пирамиды. Тогда горизонтальная проекция линий пересечения плос­кости Ф*** и граней EGG*E* и FGG*F* призмы проходит вдоль А₁С₁, через точки 9₁ и 10₁ на основании призмы. По линиям связи найдем положение точек 9₂ и 10₂ через которые проведем образующие при­змы, параллельные ее боковым ребрам. На пересечении с ребрами S₂A₂ получим точки 6₂ и 8₂. Далее по линиям связи - точки 6₁ и 8₁. Соединив одноименные проекции точек, получим фронтальную 4₂5₂6₂7₂8₂4₂ и горизонтальную 4₁5₁6₁7₁8₁4₁ проекции замкнутой ло­маной линии пересечения призмы и пирамиды. Видимость отдельных участков определяется по принципу отрезок линии пересече­ния многогранников является видимым в проекции на какую-либо плоскость, если обе грани, на которых он лежит, видимые. В связи с этим невидимые участки изображены, как показано на рис. 1.74.

Для упрощения чертежа точки 1*, 2*, 3*, 9*, 10* на правой сто­роне пирамиды (на гранях SBC и SDC) не обозначены, т. к. их построение ничем не отличается от рассмотренного выше.