1.4. Проекция плоскости.

Плоскость является простейшей поверхностью, которую можно представить как веер линий, полученных при движении прямой (об­разующей), закрепленной в некоторой точке, по другой прямой (на­правляющей).

Здесь и в дальнейшем будем рассматривать геометрические объекты, лежащие в I четверти. Тогда их горизонтальные проекции будут расположены во II квадранте, фронтальные - в I, профильные в - IV квадранте.

Способы задания плоскости на чертеже.

Рис. 1.21

Положение плоскости в пространстве может быть однозначно определено хорошо известными геометрическими объектами. В со­ответствии с этим плоскость может быть задана одним из шести спо­собов (рис. 1.21):

а) тремя точками, не лежащими на одной прямой;

б) прямой и точкой, не лежащей на этой прямой;

в) двумя параллельными прямыми;

г) двумя пересекающимися прямыми;

д) плоской фигурой;

е) следами.

На чертеже (рис. 1.21) соответствующие геометрические объекты (точки, прямые), задающие плоскость показаны в виде проекций.

П

Рис. 1.22

лоскости частного и общего положения. Плоскостью частного положения называется плоскость, занимающая частное положение в пространстве, т. е. параллельна или перпендикулярная одной из плоскостей проекций. (Рис. 1.22)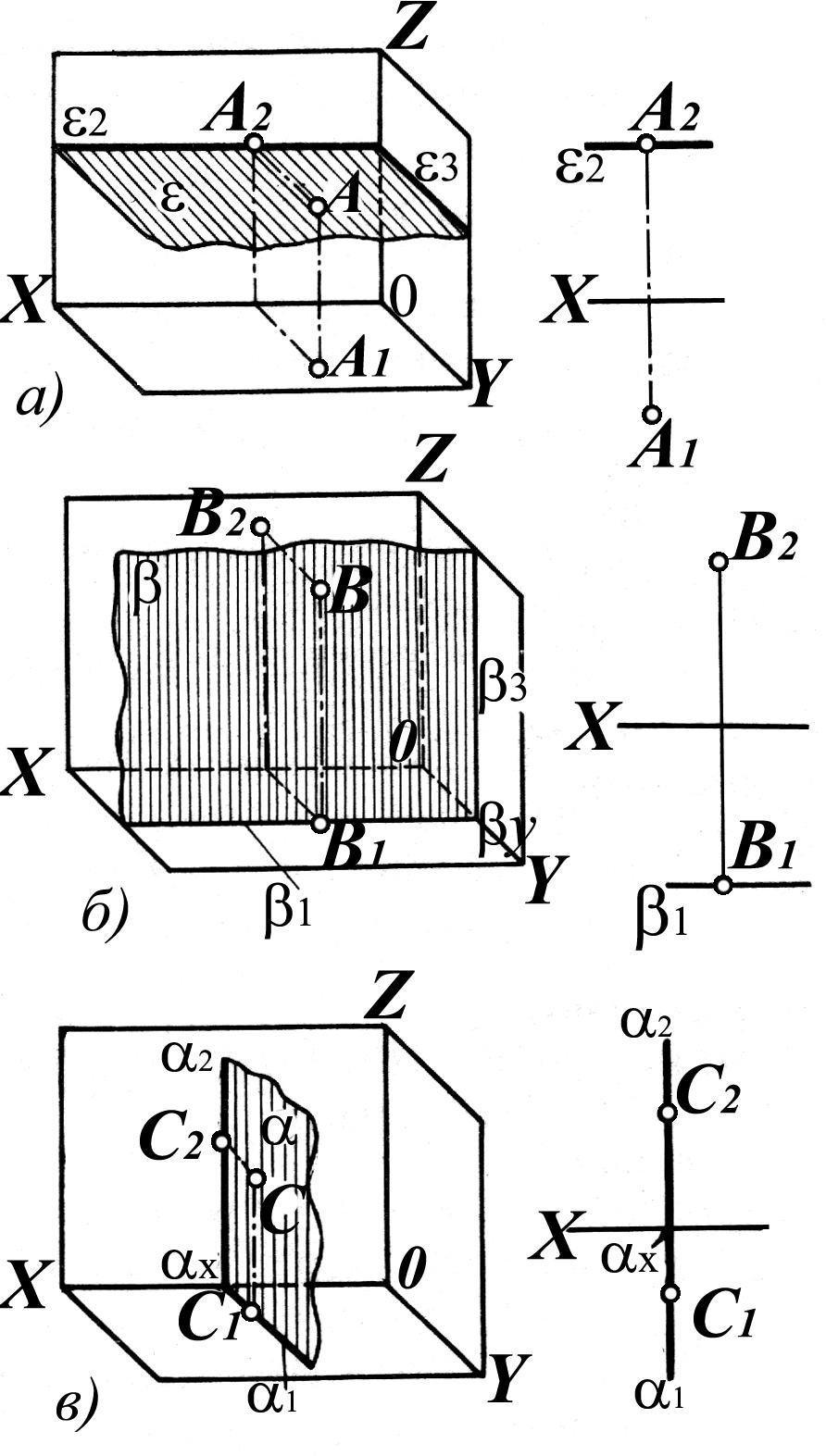

П

Рис. 1.23

лоскостью уровня называется плоскость, параллельная одной из плоскостей проекций, а следовательно, перпендикулярная двум другим Тогда проекциями плоскости уровня будут прямые, параллельные соответствующим осям (рис. 1.23), вне зависимости от того, чем задана плоскость. От способа задания плоскости зависит лишь се проекция на ту плоскость проекций, которой заданная плоскость параллельна. Плоскость, параллельная П₁ называется горизонтальной плос­костью уровня (Г), она задается тремя точками (см. рис. 1.23, а).

Плоскость, параллельная П₂ называется фронтальной плоскостью уровня (Ф). Зададим ее параллельными прямыми (см. рис. 1.23, б), причем, очевидно, расстояние от Ф, до ОХ равно расстоянию от Ф₃ до ОZ.

Плоскость, параллельная П₃, называется профильной плоскостью уровня (Р). Считаем ее заданной пересекающимися прямыми (см. рис. 1.23, в).

Плоскости общего положения. Плоскостью общего положения называется плоскость, не перпендикулярная и не параллельная ни одной из плоскостей, а значит, расположенная под произвольным углом к к

Рис. 1.24

аждой из них. У такой плоскости все проекции будут невырожденные. Например, если плоскость общего положения задана плоской фигурой (треугольни­ком), то все три проекции ее будут треугольниками. (Рис. 1.24)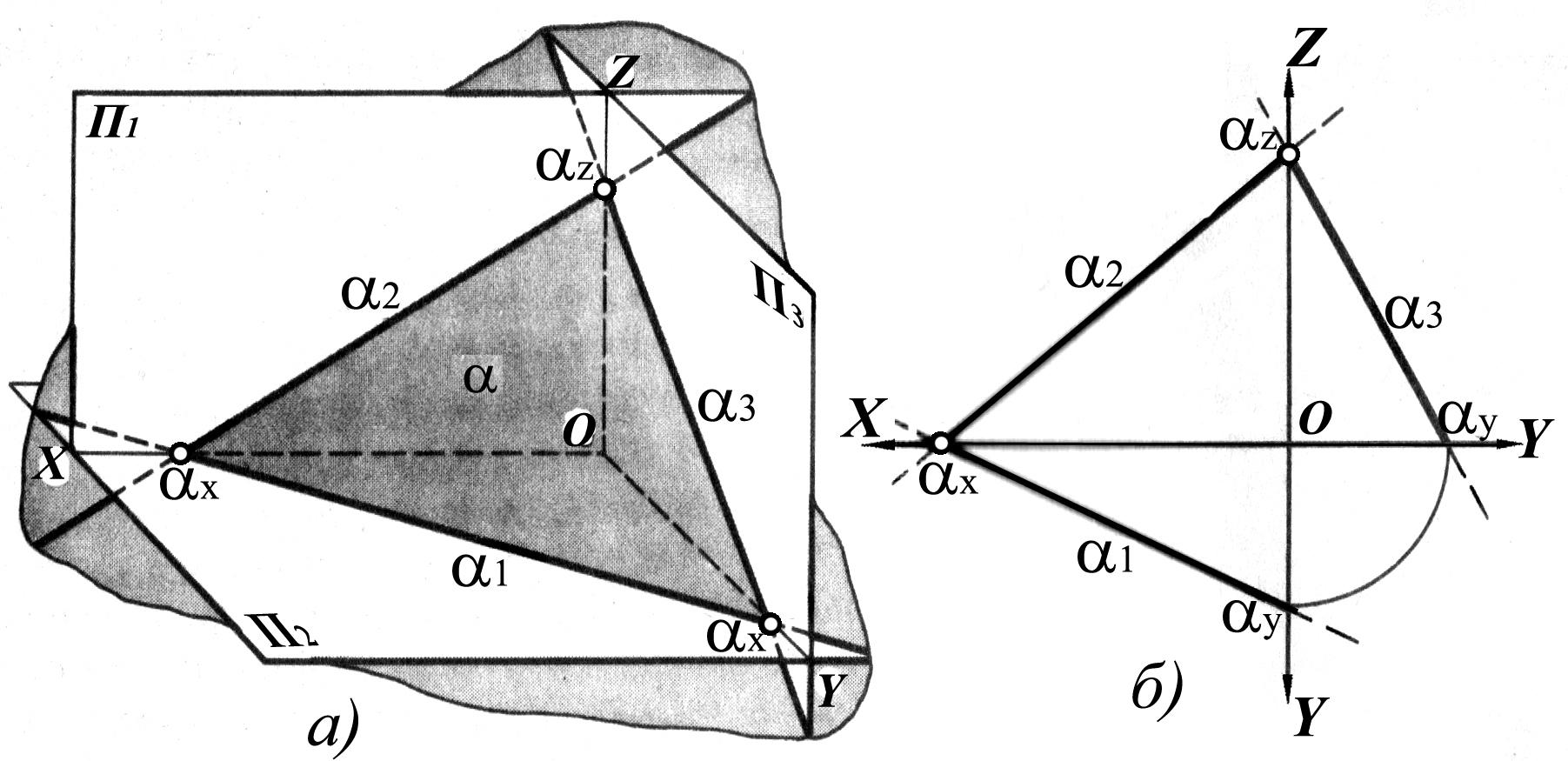

Следом плоскости называется прямая линия пересечения данной плоскости с одной из плоскостей проекций. Пересечение с П₂ дает фронтальный след плоскости, пересечение с П₁ – горизонтальный. Очевидно, что фронтальная проекция фронтального следа, так же, как и горизонтальная проекция горизонтального, совпадают с самим следом, а горизонтальная проекция фронтального следа и фронтальная проекция горизонтального лежат на оси ОХ.

Проецирующие плоскости. Проецирующей называется плоскость, перпендикулярная одной из плоскостей проекций. Исходя из определения, проекция такой плоскости является прямой при проецировании на ту плоскость про­екций, которой она перпендикулярна.

Горизонтально-проецирующей называется плоскость, перпенди­кулярная П₁, фронтально-проецирующей - перпендикулярная П₂, про­фильно-проецирующей - перпендикулярная П₃. На чертеже, первая из них задана плоской фигурой (рис. 1.25, а, б). На рис. 1.26 эта же плоскость задана следами, точка А принадлежит плоскости β, следовательно А₁ принадлежит следу β₁. Фронтально-проецирующая плоскость γ также задана следами см. рис. 1.27, а, б. Точка В принадлежит этой плоскости, следовательно В₂ принадлежит следу γ₂. На рис.1.27, в фронтально-проецирующая плоскость  задана прямой b и не лежащей на ней точкой D. Про­фильно-проецирующая плоскость ∆ задана следами. (Рис. 1.28, а, б)

Г

Рис. 1.25

Рис. 1.26

Рис. 1.27

Рис. 1.28

лавными линиями плоскости называются линии уровня, лежащие в данной плоскости.

Линии уровня плоскости. Определение линиям уровня было дано выше. Здесь к определению добавляется лишь требование принадлежности их данной плоскости.

Рассмотрим построение главных линий плоскости. (Рис. 1.29 - 1.32)

Г

Рис. 1.29

Рис. 1.30

оризонталь плоскости, заданной следами (рис. 1.29) начинаем строить с вычерчива­ния ее фронтальной проекции h₂ которая, как известно, параллель­на оси ОХ. Поскольку эта горизонталь принадлежит данной плоско­сти, то фронтальная проекция следа прямой точки А₂ принадлежит следу плоскости. Горизонтальная проекция А₁ будет находиться на оси OX и располагаться параллельно горизонтальному следу плоскости.

Горизонталь плоскости (рис. 1.31), заданной плоской фигурой - ABC, проходит через две точки треугольника, а именно, точки А и 1. Имея их фронтальные проекции А₂ и 1₂, по линии связи получим горизонтальную проекцию 1₁ (A₁ была задана). Соединив точки A₁ и 1₁, имеем горизонтальную проекцию h₁ горизонтали плос­кости ABC. Профильная проекция h₃ горизонтали плоскости ABC будет параллельна оси OY по определению.

Ф

Рис. 1.31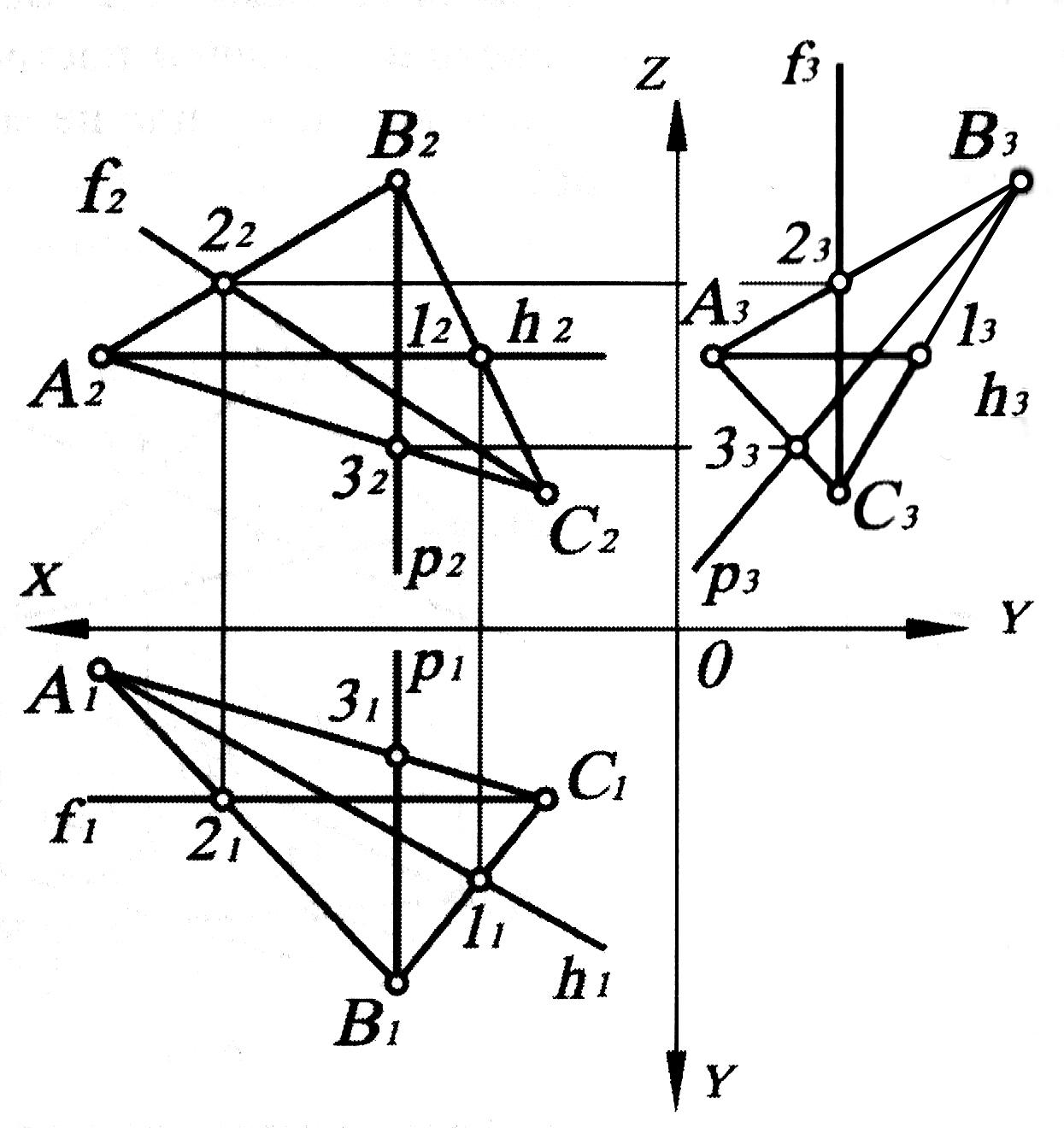

ронталь плоскости, строится аналогично горизонтали. Заданной следами см. рис. 1.30, рис. 1.29, а заданной ABC (рис. 1.31) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f₁, так как известно, что она параллельна оси ОХ. Профильная проекция f₃, фронтали должна быть параллельна оси OZ и пройти через проекции С₃, 2₃ тех же точек С и 2.

Профильная линия плоскости ABC имеет горизонтальную p₁, и фронтальную р₂ проекции, параллельные осям OY и OZ, а про­фильную проекцию р₃ можно получить по фронтальной, используя точки пересечения В и 3 в ABC.

П

Рис. 1.32

ри построении главных линий плоскости необходимо помнить лишь одно правило для решения задачи всегда нужно получить две точки, принадлежащие данной плоскости. Построение глав­ных линий, лежащих в плоскости горизонтали и фронтали, за­данной двумя пересекающимися пря­мыми, показано на рис. 1.32.

Принадлежность точки и прямой плоскости. Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.

Принадлежность прямой плоскости определяется, но одному из двух признаков:

а) прямая проходит через две точки, лежащие в этой плоскости;

б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.

Используя эти свойства, решим следующую задачу. Пусть плоскость задана ABC. Требуется построить недостающую про­екцию D₁ точки D, принадлежащей этой плоскости. На рис. 1.33 изображено последователь­ность построений проекций точки, принадлежащей плоскости.

Ч

Рис. 1.33

Рис. 1.34

ерез точку D₂ проводим проекцию прямой d, лежащей в плоскости, лежащей в плос­кости ABC, пересекающую одну из сторон треугольника и точку А₂. Тогда точка 1₂ принадлежит прямым A₂D₂ и С₂В₂. Следовательно, можно получить ее горизонтальную проекцию 1₁ на С₁В₁ по линии связи. Соединив точки 1₁ и А₁, получаем горизонтальную проекцию d₁. Ясно, что точка D₁ принадлежит ей и лежит на линии проекцион­ной связи с точкой D₂.

На рис. 1.34, а, б неизвестная проекция точки А  α, найдена с помощью горизонтали и фронтали плоскости α.

Достаточно просто решаются задачи по определению принадлеж­ности точки или прямой плоскости. Так, на рис. 1.34 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.

Для того чтобы определить, принадлежит ли точка Е плоскости ABC, проведем через ее фронтальную проекцию Е₂ прямую а₂. Считая, что прямая а принадлежит плоскости ABC, построим ее горизонтальную проекцию а₁ по точкам пересечения 1 и 2. Как ви­дим (рис. 1.35, а), прямая а₁ не проходит через точку Е₁. Следователь­но, точка ЕABC.

В

Рис. 1.35

задаче на принадлежность прямой b плоскости ABC (см. рис. 1.35, б), достаточно по одной из проекций прямой b₂ построить дру­гую – b₁*, считая, что bABC. Как видим, b₁* и b₁ не совпадают. Следовательно, прямая bABC.

П

Рис. 1.36

остроение следов плоскостей. Рассмотрим построение следов на примере плоскости, заданной треугольником ABC. (Рис. 1.36) Для решения задачи достаточно выбрать, в заданной плоскости ABC две прямые и найти точки их пересечения с П₁, и П₂, т. е. горизонтальные и фронтальные следы. Соединив эти точки на П₁ и П₂, получим искомые следы плоскости.

Рассмотрим решение задачи более подробно. В качестве указанных прямых, принадлежащих плоскости ABC , выберем АВ и ВС. Получим решение для прямой АВ. Продолжив A₂В₂ до пересечения с осью ОХ, имеем фронтальную проекцию горизонтального следа M₂. Горизонтальным следом M является точка пересечения вертикальной прямой и продолжения прямой A₁В_1. Для получения фронтального следа продолжим А₁В₁ до пересечения с осью ОХ, где лежит горизонтальная проекция фронтального следа N_1. Из этой точки проводим вертикальную прямую до пересечения с продолжением отрезка А₂В₂. Здесь и находим фронтальный след N₁.

Аналогичные построения производим для прямой ВС, получая горизонтальный M* и фронтальный N* ее следы. Соединив одноименные следы M* и M, N и N*, имеем соответственно горизонтальный α₁ и фронтальный α₂ следы плоскости ABC.

Иногда при построении возникают сложности, связанные с тем, что прямые, которыми задана плоскость, дают проекции следов, выходящие за пределы чертежа. Тогда в заданной плоскости строят любую прямую, которая позволит получить удобное решение.

Взаимное положение прямых и плоскостей. Для решения некоторых задач начертательной геометрии суще­ственное значение имеет расположение рассматриваемых геометри­ческих объектов либо параллельно, либо перпендикулярно друг другу.

Рассмотрим признаки, по которым можно определить параллельность либо перпендикулярность геометрических объектов, а также зависящие от них правила построения проекций геометрических объектов, расположенных под определенным углом друг к другу.

Параллельность прямых и плоскостей. Если прямые параллельны друг другу, тогда параллельны и их одноименные проекции. Это свойство достаточно очевидно и в рассмотрение не нуждается.

П

Рис. 1.37

рямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Тогда для построения параллельной прямой а (рис. 1.37, а) необходимо, чтобы обе ее про­екции были параллельны одноименным проекциям прямой (напри­мер, АВ), лежащей в данной плоскости. Прямая a параллельна плос­кости Н, заданной двумя пересекающимися прямыми АВ и ВС. Или в математической форме: a  Н (АВ ∩ ВС).

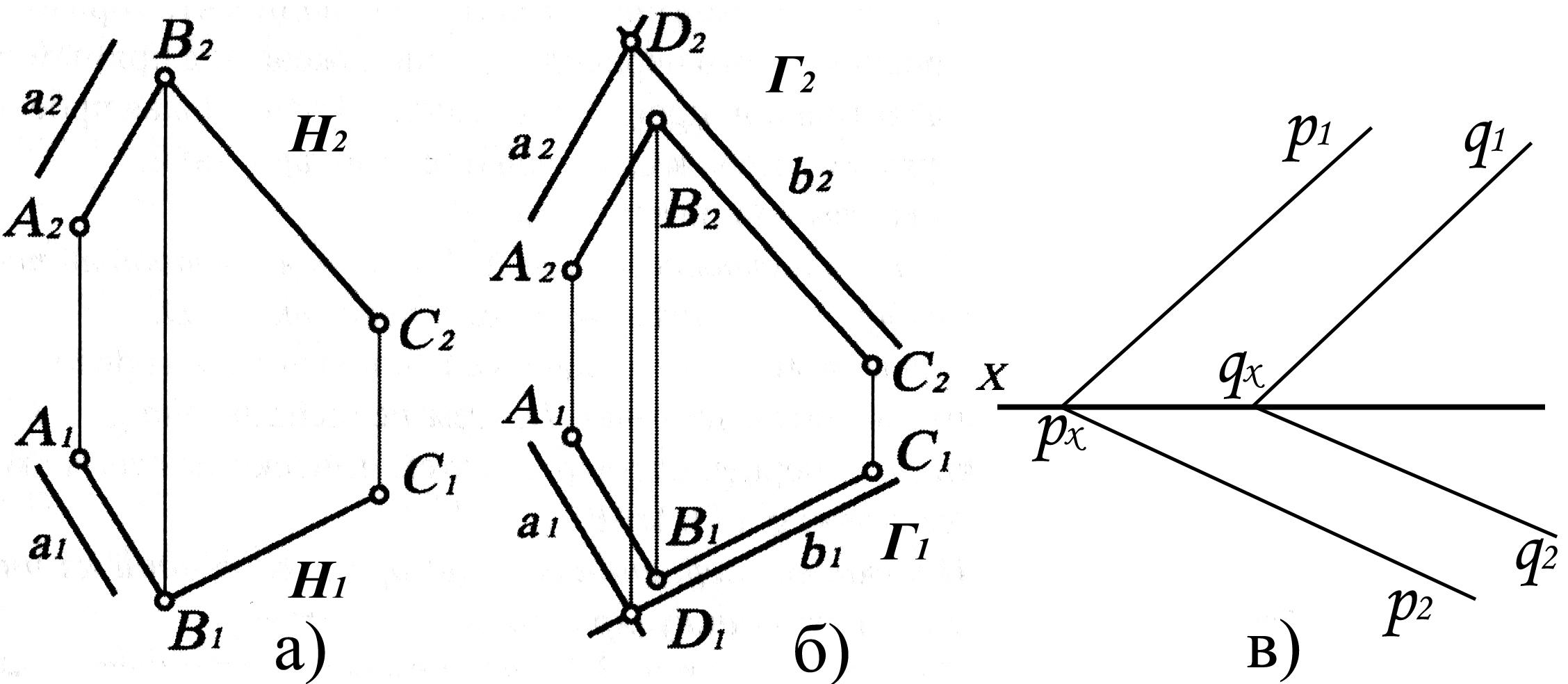
Плоскости параллельны друг другу, если две пересекающиеся прямые одной плоскости попарно параллельны двум пересекаю­щимся прямым другой плоскости. Для интерпретации этого свой­ства достаточно дополнить построения на рис. 1.37, а еще одной прямой в, пересекающей а и параллельной ВС (рис. 1.37, б). Мате­матическая запись выглядит так: Г (а∩в)  Н (АВ∩ВС).

Изображение следов плоскости p и q изображено на рис. 1.37, в.

Перпендикулярность прямых и плоскостей. Прямая перпендикулярна плоскости, если она перпендикуляр­на двум пересекающимся прямым, лежащим в этой плоскости, одна из которых фронталь, а другая горизонталь.

Д

Рис. 1.38

ля перпендикулярности достаточно, чтобы указан­ными пересекающимися прямыми были любые прямые в данной плоскости, однако только горизонталь и фронталь позволяют полу­чить без искажений проекции прямого угла, образованного перпен­дикуляром к плоскости и фронталью (на П₂) и перпендикуляром к плоскости и горизонталью (на П₁). Тогда очевидно, что горизонталь­ная проекция этого перпендикуляра расположена под прямым углом к горизонтальной проекции горизонтали, а фронтальная проекция - под прямым углом к фронтальной проекции фронтали.

Рассмотрим на примере. (Рис. 1.38, а)

Пусть плоскость задана ABC. Требуется построить перпен­дикулярную к ней прямую, проходящую через точку D.

Сначала вычертим главные линии плоскости - горизонталь и фронталь, затем из точки D₁, проведем перпендикуляр g₁, к h₁, а из точки D₂ - перпендикуляр g₂, к f₂, Математически можно записать так g  H(ABC).

Плоскости перпендикулярны друг другу, если одна из них со­держит перпендикуляр к другой.

Возвращаясь к рис. 1.38, а, где перпендикуляр к плоскости g уже построен, необходимо через точку D провести произвольную пря­мую n (рис. 1.38, б). В математической форме запись выглядит так Г(g∩n)  Н(ABC ).

Вторая прямая n проводится произвольно, так как через перпендикуляр к плоскости можно построить веер плоскостей, перпендикулярных данной.

На рис 1.38, в изображена плоскость α перпендикулярная плоскости β. Плоскость α и β заданы следами.

Прямые взаимно перпендикуляр­ны, если на одной из них можно построить плоскость, перпендикулярную другой прямой.

П

Рис. 1.39

усть требуется построить перпендикуляр к прямой g, проходящий через точку А. Следуя вышеуказанному признаку, сначала нужно построить и плоскость, перпендикулярную g и проходящую через точку А. Эта плоскость будет задана фронталью f и горизонталью h, причем h₁g₁ u f₂g₂, а проек­ции h₂ и f₂, проводим параллельно оси ОХ. (Рис. 1.39)

Любая прямая, лежащая в этой плоскости, будет перпендикулярна g, например прямая АВ, полученная по точкам пересечения 1 и 2 с плоско­стью, заданной h и f. При решении этой задачи учитываем, что если мы хотим построить пересекающиеся перпендикулярные прямые, тогда прямая AВ должна быть построена единственным образом. А именно, сначала требуется найти точку В, пересечения g и плоскости H (h∩ f), затем провести АВ. В нашем случае АВ выбра­на произвольно и точка В не является точкой пересечения g и плос­кости H (h∩ f).

Позиционные задачи на плоскости. Позиционными называются задачи на определение каких-либо общих элементов геометрических объектов, например, точки пере­сечения прямой и плоскости, линии пересечения двух плоскостей.

Пересечение прямой и плоскости. Задачу на пересечение прямой и плоскости можно решать с по­мощью вспомогательной секущей плоскости, которая должна удовлетворять следующим условиям (рис. 1.40, 1.41):

- быть плоскостью частного положения, так как именно плос­кость частного положения проецируется на соответствующую плос­кость проекций в виде прямой;

- проходить через прямую, точку пересечения, которой с плоско­стью мы отыскиваем.

П

Рис. 1.40

усть, например, даны прямая а и горизонтально проецирующая плоскость β (см. рис. 1.40, а). Тогда горизонтальная проекция К₁ искомой точки должна одновременно лежать на горизонтальной проекции β₁ плоскости β и на горизонтальной проекции β₁ прямой а, т. е. в точке пересечения а₁ с β₁ (К₁ = а₁∩ β₁). (Рис. 1.40, б) Фронтальная проекция К₂ точки К расположена на ли­нии проекционной связи и на фронтальной проекции β₂ прямой а.

Теперь рассмотрим один из частных слу­чаев пересекающихся плоскостей, когда одна из них — проецирующая.

На рис. 1.41, а приведены плоскость общего положения, заданная треугольником ABC, и горизонтально проецирующая плоскость α. Найдем две общие точки для этих двух плоскостей. Этими общими точ­ками для плоскостей ABC и α будут точки пересечения сторон АВ и ВС треу­гольника ABC с проецирующей плоско­стью α. Построение таких точек D и Е как на пространственном чертеже (рис. 1.41, а), так и на эпюре (рис. 1.41, б) производится а

Рис. 1.41

налогично.

Соединяя одноименные проекции точек D и Е, получим проекции линии пересече­ния плоскости ABC и плоскости α.

Таким образом, горизонтальная проек­ция D₁E₁ линии пересечения заданных плоскостей совпадает с горизонтальной проекцией проецирующей плоскости α — с ее горизонтальным следом α₁.

При решении задач на пересечение прямой с плоскостью следует выделить частный случай. Если плоскость зани­мает проецирующее положение, то одна проекция точки пересечения опреде­ляется в пересечении проекции прямой с проекцирующим следом плоскости, а другая проекция строится с помощью линии связи.

Рассмотрим примеры решения следующих задач.

П

Рис. 1.42

усть плоскость занимает частное положение в пространстве, например, является горизонтально-проецирующей и задана ABC (рис. 1.42, а). Необходимо найти точку пересечения ее с прямой а, заданной произвольно. Поскольку на П₁ горизонтально—проециру­ющая плоскость вырождается в прямую, то горизонтальной проек­цией точки пересечения будет К₁. Далее по линии связи на прямой α₂ (очевидно, что точка пересечения К принадлежит прямой α) най­дем фронтальную проекцию К₂ точки пересечения.

Осталось определить видимые участки прямой а, поскольку на П₂ часть указанной прямой будет закрыта от наблюдателя плоско­стью ABC. Для этого необходимо рассмотреть точку, где пересекаются фронтальные проекции а с какой-либо прямой (например, АС), лежащей в плоскости ABC. Обозначим эту точку 1₂. Но пересекать­ся прямая а и ABC могут только в одной точке, которую мы отыс­кали (К₂). Все остальные будут точками, где они скрещиваются. Сле­довательно, прямые а и АС скрещиваются в пространстве. Значит, все точки, где пересекаются их проекции, будут конкурирующими, а именно 1₂ ≡ 2₂. Тогда на П₁ имеем по линии связи 1₁  A₁С₁ и 2₁  а₁. Видимой является точка 2, которая принадлежит прямой а. Это вы­полняется до точки пересечения К₂. Затем, естественно, участок прямой а будет невидим (обозначается пунктирной линией) до вы­хода из-под плоскости ABC. Теперь задачу можно считать решенной.

Р

Рис. 1.43

ассмотрим общий случай пересечения прямой и плоскости, ког­да обе они занимают общее положение в пространстве.

Если заданна плоскость общего по­ложения, точка пересечения прямой с плоскостью определяется с помощью вспомогательной секущей плоскости. (Рис. 1.43, построение - рис. 1.44)

Для построения точки пересечения прямой линии с плоскостью необходи­мо:

1) провести через прямую DE вспо­могательную проецирующую плоскость S (рис. 1.44, а);

2) построить линию MN пересечения данной плоскости и вспомогательной (рис. 1.44, б);

3) определить искомую точку К пересечения данной прямой DE с ли­нией пересечения плоскостей MN (рис. 1.44, в).

Р

Рис. 1.44

ешение задачи завершается опреде­лением видимых участков прямой. Видимость прямой относительно плоско­сти треугольника определяют путем разбора взаимоположения точек задан­ной прямой и сторон плоскости треу­гольника, совпадающих на проекциях, как было рассмотрено на рис. 1.42.

Задача на пересечение прямой с пло­скостью решается аналогичным обра­зом и в том случае, когда плоскость за­дана следами. (Рис. 1.45)

П

Рис. 1.45

усть теперь необходимо найти точ­ку пересечения произвольно заданной прямой b с ABC. (Рис. 1.45, а)

Как рассматривалось выше, нужно через прямую b провести плоскость частного положения (например, фронтально-проецирующую). Ли­ния пересечения этой плоскости совпадает с прямой b на П₂, т. е. ₂ = b ₂. Тогда по точкам пересечения 3₂ и 4₂ построим точки 3₁ и 4₁, а следовательно, и прямую 3₁,4₁, являющуюся горизонтальной проек­цией линии пересечения плоскости  и ABC. Так как прямая 3 4ABC , то точка К₁ будет горизонтальной проекцией точки пересе­чения прямой b и ABC. По ней найдем и фронтальную проекцию К₂, которая, очевидно, должна быть расположена на b ₂ (ведь точка пересечения принадлежит и прямой b и ABC).

Определим видимые участки прямой b на обеих проекциях по конкурирующим точкам Для определения видимости на П₂ исполь­зуем фронтально-конкурирующие точки (например, точки 3₂=5₂, где скрещиваются b и АВ) Очевидно, что точка 3₁ ближе к нам, чем точка 5_l. Следовательно, на П₂ выше 3₂ тогда в этой точке А₂В₂ выше, а b₂ лежит под ней. Это верно только до точки пересечения К₂. Да­лее, естественно, выше будет b₂. Аналогично по горизонтально-кон­курирующим точкам (например, 6₁=7₁) определяем, что в точках 6₁=7₁ прямая B₁C₁ лежит выше, чем b₁, так как точка 7₂ расположена выше, чем точка 6₂. Невидимый участок прямой b обозначаем пунктирной линией.

Следует иметь в виду, что когда плоскость задана не плоской фигурой, можно говорить лишь о видимости отдельных участков прямой относительно плоскости, хотя такая постановка задачи вер­на и в случае плоской фигуры.

П

Рис. 1.46

редыдущую задачу можно сформулировать несколько иначе: определить видимость участков прямой b относительно точки ее пересечения с плоскостью, которая задана ABC , а не с самим ABC. Тогда невидимые участки левее точки К₂ и правее K₁ мы долж­ны были бы продлить до бесконечности.

Более наглядно эту особенность можно проинтерпретировать на примере (рис. 1.46, б), где плоскость задана пересекающимися пря­мыми а и b. Ход решения не отличается от предыдущего, но невидимость участков прямой с уже не ограничена геометрически­ми элементами, задающими плоскость.

Таким образом, чем бы ни была задана плоскость, точку ее пере­сечения с прямой можно найти, используя секущую плоскость част­ного положения, проходящую через эту прямую, а видимость (или невидимость) на плоскостях проекций отдельных участков прямой - с помощью конкурирующих точек.

Пересечение плоскостей. Метод вспомогательных секущих плоскостей. Поскольку линией пересечения двух плоскостей является пря­мая, то для ее построения необходимо определить лишь две точки пересечения плоскостей.

Для решения указанной задачи применяется метод вспомога­тельных секущих плоскостей, который заключается в следующем.

В

Рис. 1.47

водятся две дополнительные плоскости, пересекающие задан­ные. Для каждой дополнительной (вспомогательной) плоскости строим линию ее пересечения с заданными плоскостями Точка пересечения двух полученных линий и будет точкой пересечения заданных плоскостей Поскольку дополнительных плоскостей две, то и точек пересечения заданных плоскостей тоже две Соединяя их, получаем линию пересечения плоскостей Разумеется, каждая дополнительная плоскость должна занимать частное положение в пространстве, тогда на плоскость проекций, к которой вспомогательная плоскость перпендикулярна, она проецируется в прямую. Иначе, если вспомогательная плоскость занимает общее положе­ние, введение дополнительной плоскости не упрощает решение задачи.

Рассмотрим на примерах общий случай. Пусть в пространстве заданы две плоско­сти общего положения α и β (рис. 1.47). Для построения линии их пересечения не­обходимо, как отмечалось выше, найти две точки, общие обеим плоскостям.

Для определения этих точек заданные плоскости пересекают двумя вспомогательными плоскостями. В качестве таких плоскостей целесообразнее взять прое­цирующие плоскости и, в частности, плоскости уровня. На рис. 1.47 первая вспомогательная плоскость уровня γ каж­дую из данных плоскостей пересекает по горизонталям h и h¹, которые определяют точку 1, общую для плоскостей α и β, а значит, и принадлежащую линии их пересечения. Взяв вторую вспомогатель­ную плоскость , например, также парал­лельную П₁, получим еще одну точку — 2, общую плоскостям П₁. Эта точка опре­деляется пересечением горизонталей h² и h³, по которым вспомогательная плос­кость  пересекает каждую из данных плоскостей.

О

Рис. 1.48

писанный метод применен для эпюр построения проекций линии пересече­ния двух плоскостей, первая из которых задана двумя параллельными прямыми, а вторая — тремя точками. (Рис. 1.48) С по­мощью вспомогательной плоскости γ най­дена точка 1 как точка, в которой пересе­каются горизонтали h u h₁. Точно так же с помощью плоскости  определена вторая точка — 2.

Некоторого упрощения можно достичь, если вспомогательные проецирующие плоскости проводить через прямые, задающие плоскость, что и сделано на рис. 1.49, где построена линия 1—2 пересечения плоскостей α (ABC) и β (DEF). Точка 1 этой линии определена с помощью фрон­тально проецирующей плоскости γ, прове­денной через сторону DE треугольника DEF. Именно эта сторона, проекции кото­рой заданы, и является линией пересечения плоскости DEF и γ (DE = β ∩ γ).

У

Рис. 1.49

прощение графического решения состоит в том, что не нужно чертить эту прямую, входящую в число элементов, задающих плоскость β.

Та же плоскость γ пересечет второй треугольник ABC по прямой KL (KL = γ∩α).Аналогично, проведя через сторону ВС горизонтально проецирующую плоскость , найдем точку 2. На рис. 1.49 прямая ВC = ∩α, а MN=∩β. Пересечение этих прямых определяет точку 2. Причем ее фронтальная проекция 2₂ строится раньше, чем 2₁. Точки 1 и 2 являются точками пересечения сторон одного треугольника.