
- •«Начертательная геометрия»
- •1. Основы начертательной геометрии
- •1.1. Методы проецирования.
- •1.2. Проекция точки.
- •1.3. Проекция прямой.
- •1.4. Проекция плоскости.
- •1.5. Способы преобразования ортогонального чертежа.
- •1.6. Многогранники.
- •1.7. Поверхности вращения.
- •1.8. Развертки поверхностей геометрических тел.
- •1.9. Аксонометрические проекции.
1.2. Проекция точки.
Э
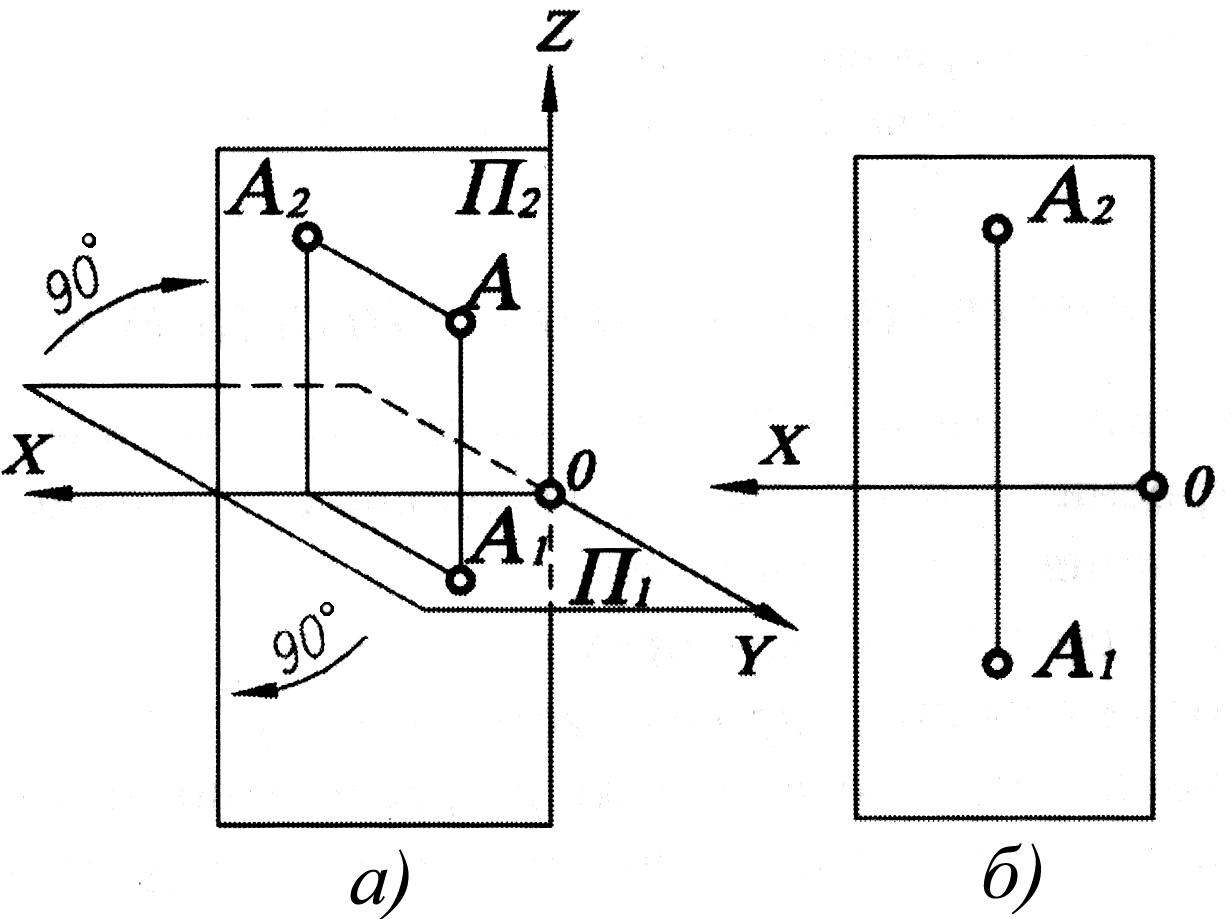 Рис.
1.4
Рис.
1.4
Несмотря на наглядность, с чертежом, где проекция точки А расположена в пространстве (рис. 1.4, а), работать неудобно, т. к. горизонтальная плоскость на нем показана с искажением. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость развернуть вокруг оси OX на 90° и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя – вверх. Этот метод предложил Г. Монж, поэтому чертеж, полученный таким образом (рис. 1.4, б) называется эпюром Монжа или комплексным чертежом.
О
 Рис.
1.5
Рис.
1.5
Оси OX, OY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево. Теперь, чтобы получить проекции в одной плоскости (плоскости чертежа), необходимо и профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. В результате получим трехкартинный комплексный чертеж (эпюр Монжа), показанный на рис 1.5, б. Так как ось OY разворачивается вместе с двумя плоскостями П1 и П3, то на комплексном чертеже ее изображают дважды.
Исходя из рис. 1.5, а, очевидно, что А1Ах = OAy = АzА3. Из этого следует важное правило взаимосвязи проекций: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции точки до оси OZ. Тогда по двум любым проекциям точки можно построить третью. Горизонтальную и фронтальную проекции точки А связывает вертикальная линия связи, а фронтальную и профильную проекции – горизонтальная.
В связи с тем, что комплексный чертеж представляет собой свернутую в плоскость модель пространства, на нем нельзя изобразить проецируемую точку (за исключением случаев, когда ее положение совпадает с одной из проекций). На комплексном чертеже мы оперируем не самими геометрическими объектами, а их проекциями.
Ортогональная система трех плоскостей проекции. Выше было показано, что две проекции точки определяют ее положение в пространстве. Так как каждая фигура или тело представляет собой совокупность точек, то можно утверждать, что и две ортогональные проекции предмета (при наличии буквенных обозначений) вполне определяют его форму.
Однако в практике для изображения изделий, машин и различных инженерных конструкций возникает необходимость в создании дополнительных проекций. Поступают так с единственной целью — сделать проекционный чертеж более ясным, удобочитаемым.
Модель трех плоскостей проекций показана на рис. 1.6, а. Третья плоскость, перпендикулярная П1 и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость будут также именоваться профильными.
Плоскости проекций, попарно пересекаясь, определяют три оси: OX, OY, OZ, которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке О. Три плоскости проекций делят пространство на восемь трехгранных углов — это так называемые октанты.
Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте.
Д
Рис. 1.6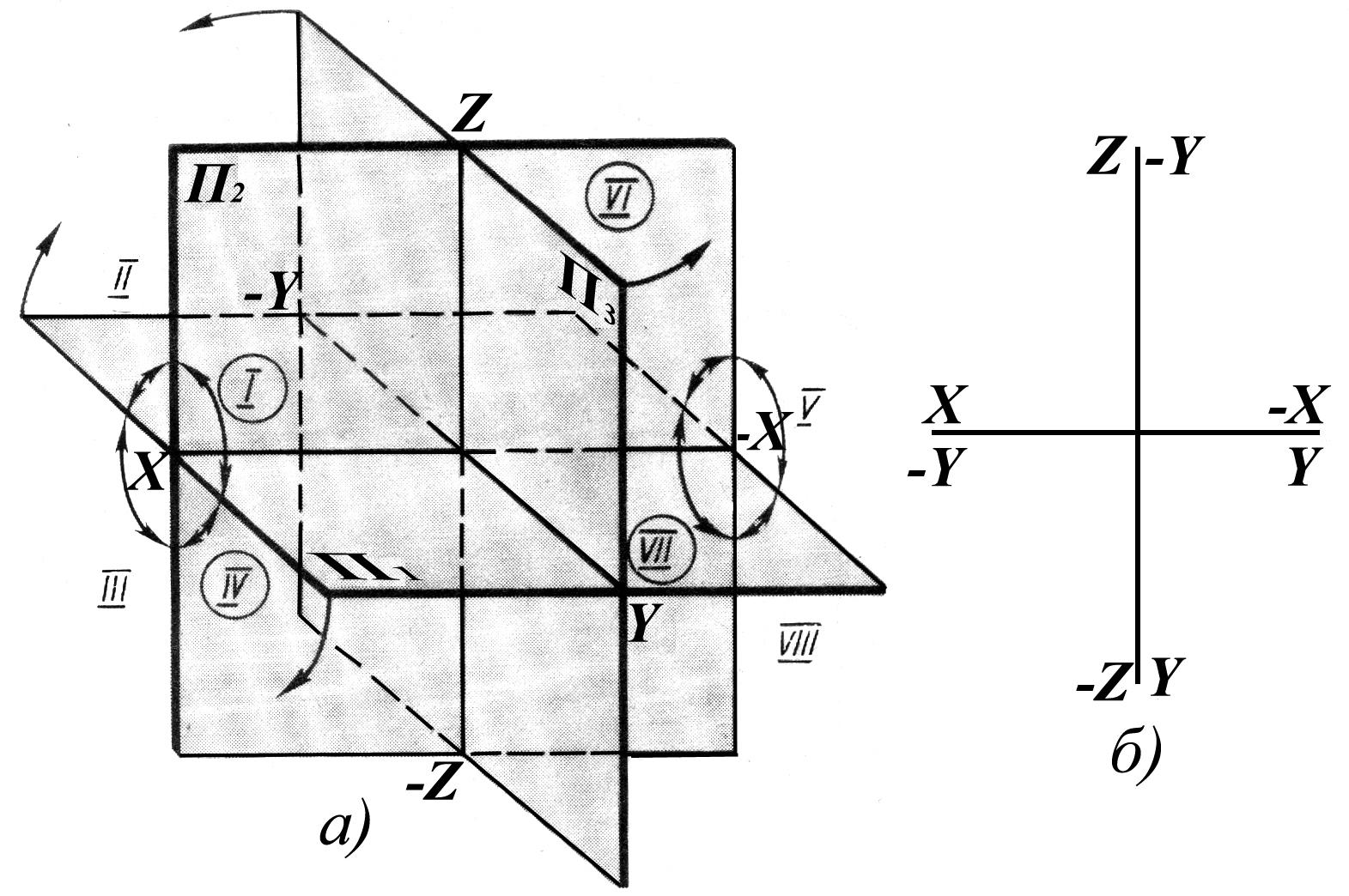
О
Табл.1.1 Октант
Знаки
координат
I + + + II + - + III + - - IV + + - V - + + VI - - + VII - - - VIII - + -
В дальнейшем при обозначении осей на эпюре отрицательные полуоси (— OX; — OY; — OZ) указываться не будут. Окончательный вид всех совмещенных плоскостей проекции (октант) даны в табл. 1.1.
П
Рис. 1.7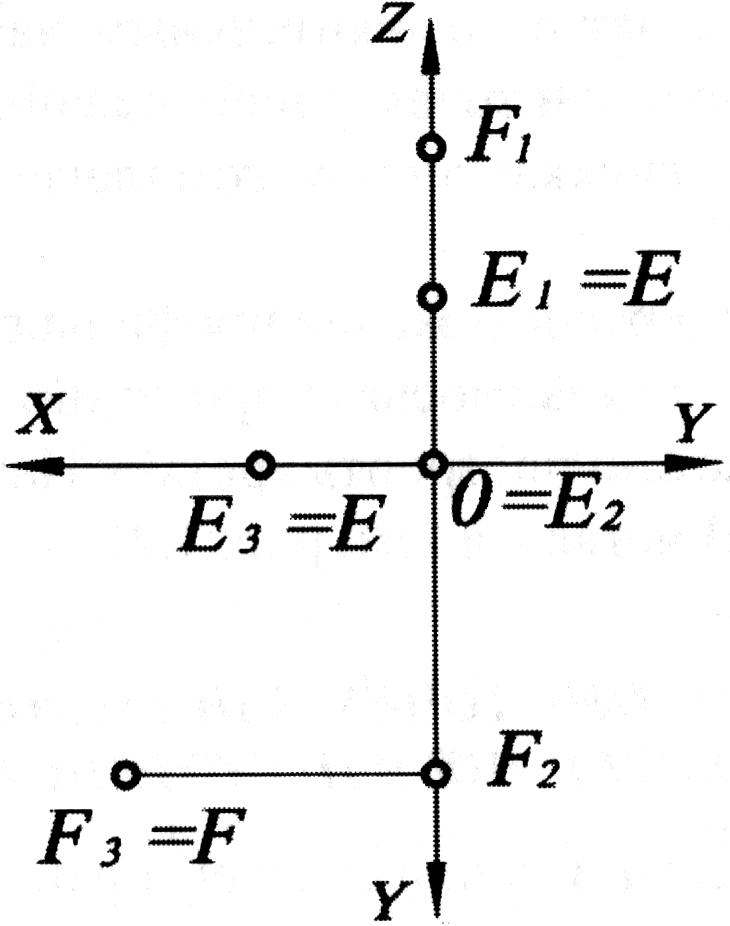
В качестве примера рассмотрим построение проекций точки Е, принадлежащей оси OY и расположенной во II четверти, и точки F, лежащей в профильной плоскости проекций и расположенной в III четверти. (Рис. 1.7)
Для точек, занимающих частное положение в пространстве, построения следует начинать с проекций, принадлежащих либо оси, либо плоскости проекций.
П
Рис. 1.8
Взаимосвязь координат точки и ее проекций показаны на рис. 1.8, где 1.8, а - вид в аксонометрии, 1.8, б - комплексный чертеж.
Необходимо помнить, что положение горизонтальной проекции определяется координатами х и у, фронтальной проекции - координатами х и z, профильной проекции координатами у и z. Тогда ордината у всегда характеризует положение горизонтальной проекции, а аппликата — фронтальной.
Исходя из тех же положений, решается обратная задача — определение координат точки по ее проекциям. Если на комплексном чертеже изображены проекции точки, тогда, измерив, соответствующие расстояния, определяем ее координаты (см. рис. 1.8, б) Причем для определения всех трех координат достаточно двух проекций, т. к. любая пара проекций определяет три координаты.
Удаленность точки от плоскости проекций. Расстояние точки от какой-либо плоскости проекций определяет положение соответствующих проекций, а именно расстояние до П1 характеризует положение фронтальной проекции расстояние до П2 горизонтальной проекции, расстояние до П1 - и горизонтальной и фронтальной проекций. Так, если известно, что точка А удалена от П1, на 30 мм, тогда ее фронтальная проекция А2 удалена от оси ОХ на 30 мм, если задано, что точка А удалена от П3 на 10 мм, тогда А1, и А2, удалены от осей OZ и OY соответственно на это расстояние (см. рис. 1.8).
Е
Рис. 1.9
Рис. 1.10


Симметрия. Симметричными относительно плоскости проекций считаются точки, расположенные на одинаковом расстоянии от нее, но с разных сторон. При этом меняется знак соответствующих координат точки. Например, пусть задано положение точки А. Требуется построить точку М, симметричную точке А (см. рис. 1.8, б) относительно плоскости П2, и точку N. симметричную точке А относительно плоскости П1. Тогда проекции этих точек будут расположены на комплексном чертеже, как показано на рис. 1.10.
