§ 12.6 Понятия языка и грамматики. Алгоритм и машина Тьюринга
С помощью конечного автомата можно реализовать, например, алгоритм сложения дух чисел. Однако не каждый алгоритм допускает реализацию в виде конечного автомата.
Для расширения понятия автомата как инструмента реализации алгоритмов нам понадобится ряд понятий.
Определение
Конечное
число элементов
назовем словарем;
элементы словаря называются символами
(словами);
последователь ности символов называются
цепочками
(предложениями);
множест во выделенных предложений
называется языком
над словарем
.
Обозначение
- язык над словарем
;
- множество всех цепочек.
Определение Грамматикой называется конечный механизм задания языка.
Приведем два таких механизма.
Определение
Порождающей
грамматикой языка
называет ся конечный набор правил,
позволяющий строить правильные предло
жения
и только их.
Определение
Распознающей
грамматикой языка
называется
критерий принадлежности данной цепочки языку.
Роль распознающей грамматики может выполнять следующий автомат без выходов.
Определение
Конечным автоматом-распознавателем
называется пятерка
,
где
- конечное множество состояний,
-
входной алфавит,
-
начальное состояние,
- функция переходов,
- множество финальных
состояний.
Конечный автомат-распознаватель
допускает
цепочку
,
то есть
,
тогда и только тогда, когда
переводит его из состояния
в состояние
.
Определение Язык, для которого существует распознающий его автомат-распознаватель, называется автоматным языком.
_____
Определение Алгоритм – определенное на некотором языке конечное предписание (рецепт), задающее дискретную последователь ность исполняемых элементарных операций для решения задачи.
ЗАМЕЧАНИЕ Существует несколько формальных моделей
алгоритма: Геделя, Черча, Тьюринга, Маркова. Доказано, что
алгоритм, реализуемый в одной из этих моделей, реализуем и в
остальных.
Конечный
автомат-распознаватель выполняет
преобразование информации по определенным
правилам, то есть реализует некоторый
алгоритм обработки информации. Один из
главных вопросов информа тики –
построение автоматического устройства,
реализующего алгори тмы. Мы показали,
что не существует автомата-распознавателя,
реализующего алгоритм задания языка
,
,
как и не существует автомата, реализующего
алгоритм умножения двух произвольных
чисел. Для того чтобы обобщение понятия
авто матно реализуемых алгоритмов было
более наглядным, рассмотрим
такую «механическую» интерпретацию конечного автомата-распознавателя.
ЗАМЕЧАНИЕ Конечный автомат (КА) – это устройство с
конечным числом внутренних состояний, одним входом и одним
выходом. Вход реализован в виде считывающей головки, которая
движется вдоль входной ленты и потактово считывает содержимое
ее
ячеек (буквы
).
Выход
реализуется
виде печатающей голов
ки, которая синхронно движется вдоль выходной ленты и печатает
на
ней выходной символ
.
При этом внутреннее состояние
автомата
меняется с
на
.
Функционирование КА, то есть его
программа, вполне определяется заданием вход-выходного отобра
жения
с
.
Определение
Машиной
Тьюринга (МТ)
называется устройство с 1) одной
бесконечной
лентой, с
которой считываются входные и куда
впечатываются выходные символы, 2) одной
головкой
чтения-записи, которая может двигаться
по рабочей ленте в любую сторону. На
каждом такте МТ считывает символ
из обозреваемой ячейки и:
1)
изменяет свое состояние (на
)
в зависимости от этого символа
и
текущего
состояния
,
2)
впечатывает символ
в обозреваемую ячейку и
3)
головка чтения записи перемещается в
направлении
:
влево (
),
вправо
(
)
или остается на месте (
).
Функционирование
МТ, то есть программа
машины Тьюринга
– это конечный список пятерок
,
порождающих частичное отображение
,
где
- входной и
одновременно выходной алфавит,
.
Если в этой программе нет пары
,
то машина останавливается. На ленте
присутствует знак "Останов"
,
который отделяет цепочки значащих
символов.
При таком определении машина Тьюринга "перерабатывает" (заменяет) входную цепочку на выходную. То есть она является автоматом-преобразователем отдельных цепочек.
ЗАМЕЧАНИЕ
Машина
Тьюринга реализует алгоритм перемножения
произвольных чисел. В качестве
распознавателя МТ распознает, например,
язык
.
Программой такой МТ является множество
пятерок
.
Здесь
- финальное состояние. Ее граф имеет вид
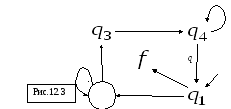
Определение Проблема называется алгоритмически неразре шимой, если машина Тьюринга не распознает язык этой проблемы.
Пример Ю. Матиясевич доказал, что 10-ая проблема Гильберта алгоритмически неразрешима.