
- •Е.В. Бондарева
- •§1. Элементы теории множества. Абсолютная величина действительного числа.
- •§2. Комплексные числа.
- •§3. Функция. Свойства функции. Преобразования графиков.
- •§4. Последовательность. Предел последовательности.
- •§5, §6. Предел функции. Техника вычисления пределов Найти пределы:
- •§ 7. Непрерывность функции.
- •§ 8. Производная.
- •§9. Дифференцирование неявно заданных функций.
- •§ 10. Логарифмическое дифференцирование.
- •§12. Дифференциал функции.
- •§13. Дифференцирование функций, заданных параметрически.
- •§14. Производные и дифференциалы высших порядков.
- •§15. Применение производной к исследованию функции.
- •§16. Функции многих переменных.
- •4. Найти .
- •5. Найти
- •9. . Найти .
- •§17 Экстремум функции двух переменных
§13. Дифференцирование функций, заданных параметрически.
|
|
Н![]()
![]()
![]() айти
айти
![]()
Найти
![]() при указанном значении t.
при указанном значении t.
|
9)
|
10)
|
§14. Производные и дифференциалы высших порядков.
1.
Найти
![]() функции у,
если
функции у,
если
1)
![]() ; 2)
; 2)
![]() .
.
|
|
2.
Найти
![]() функции у,
если
функции у,
если
3. Найти дифференциалы указанных порядков для заданных функций:
|
|
§15. Применение производной к исследованию функции.
Основные теоремы дифференциального исчисления
1.
Определить с
в формуле Лагранжа для функции
![]() на отрезке
на отрезке
![]() .
.
2.
Написать формулу Коши для функции
![]() и
и
![]() и определить значение с
на отрезке [-2;1].
и определить значение с
на отрезке [-2;1].
|
|
|
3![]()
![]()
![]()
![]() .
Пользуясь правилами Лопиталя, найти
указанные пределы:
.
Пользуясь правилами Лопиталя, найти
указанные пределы:
4. Исследовать на монотонность и экстремум функции:
|
|
5. Найти наибольшее и наименьшее значения функции на данном отрезке:
|
|
6.
При подготовке к экзамену студент за
t
дней изучает
![]() -ю
часть курса, а забывает
-ю
часть курса, а забывает
![]() -ю
часть. Сколько дней нужно затратить на
подготовку, чтобы была изучена
максимальная часть курса? Решить
задачу при
-ю
часть. Сколько дней нужно затратить на
подготовку, чтобы была изучена
максимальная часть курса? Решить
задачу при
1)
![]() ,
,
![]() ; 2)
; 2)
![]() ,
,![]() .
.
7. Требуется изготовить закрытый цилиндрический бак с заданным объемом V. Каковы должны быть размеры бака, чтобы его полная поверхность была наименьшей?
8. В данный прямой круговой конус вписать цилиндр наибольшего объема.
9. Данное положительное число а разложить на два слагаемых так, чтобы произведение их было наибольшим.
10. Найти точки перегиба и определить интервалы выпуклости кривой:
|
|
11. Найти асимптоты кривой:
|
|
Индивидуальное задание по теме: «Исследование функции и построение графика»
Исследовать функцию и построить график.
Исследование функции проводить по следующей схеме:
-
Найти область определения функции;
-
Исследовать функцию на непрерывность. Найти точки разрыва функции и ее односторонние пределы в этих точках;
-
Найти (если можно) точки пересечения графика функции с осями координат;
-
Выяснить, является ли функция четной, нечетной или общего вида;
-
Исследовать на монотонность и экстремум;
-
Найти интервалы выпуклости и точки перегиба графика функции;
-
Найти асимптоты графика функции;
-
Используя результаты исследования построить график.
-
Найти наибольшее и наименьшее значения функции №1 на отрезке
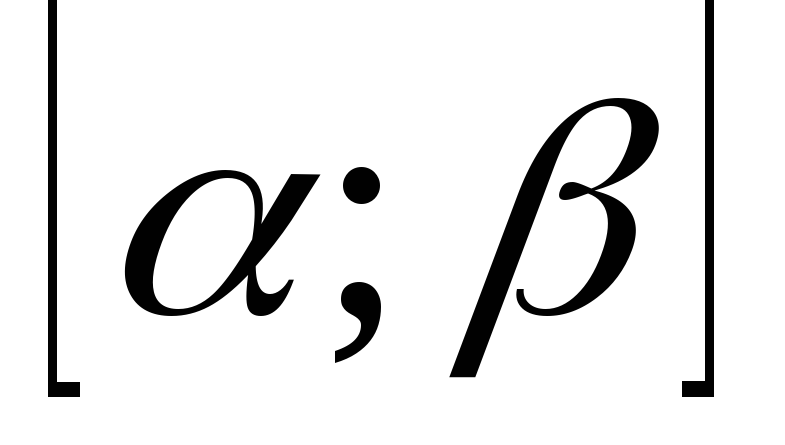
|
|
|

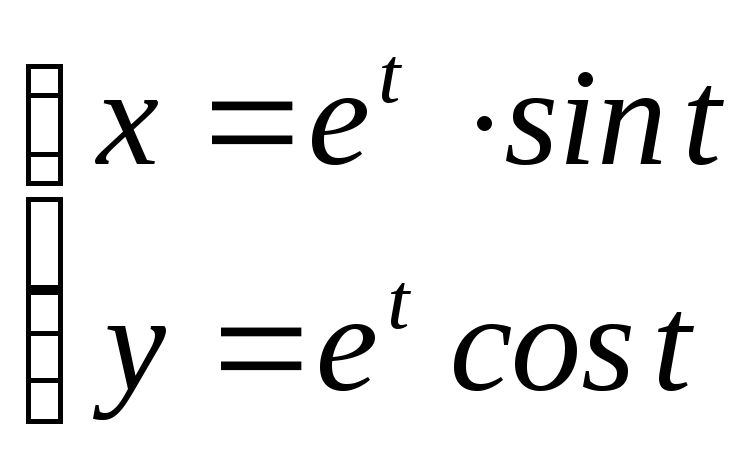 ;
;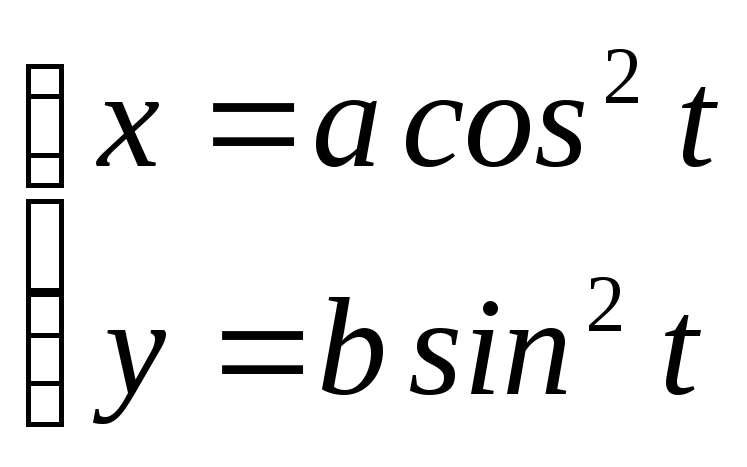 ;
;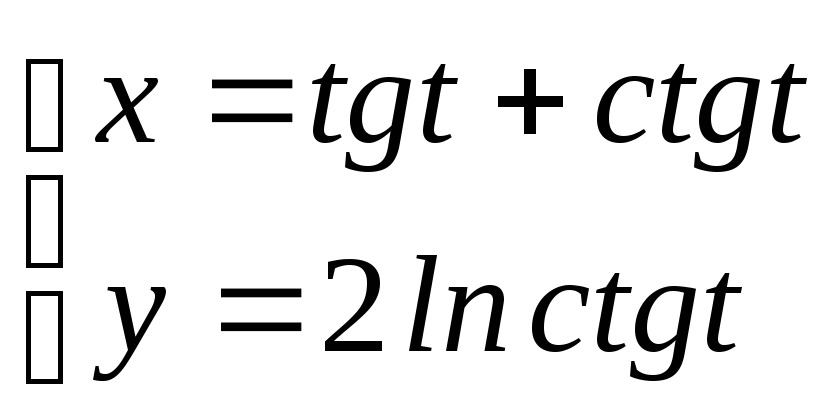 ;
; ;
;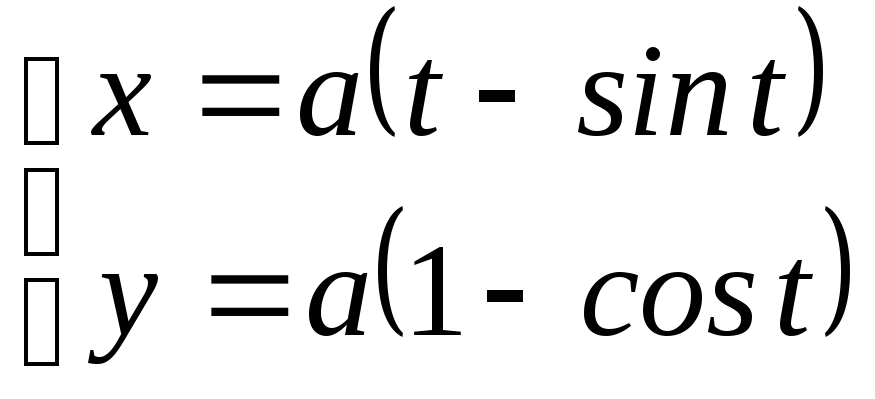 ;
;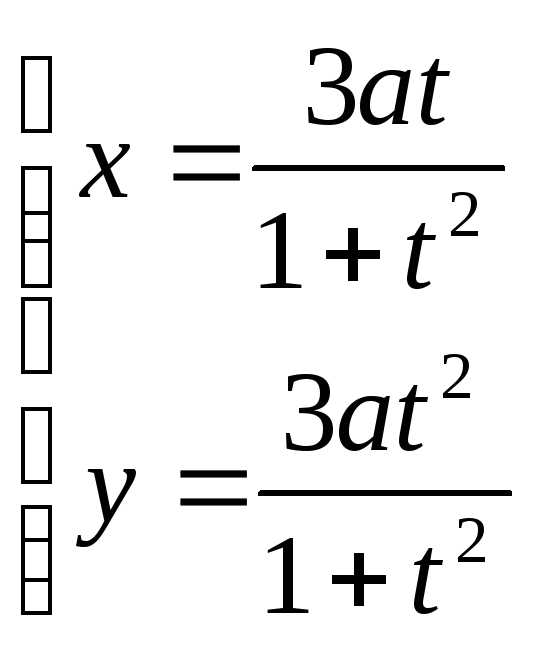 ;
;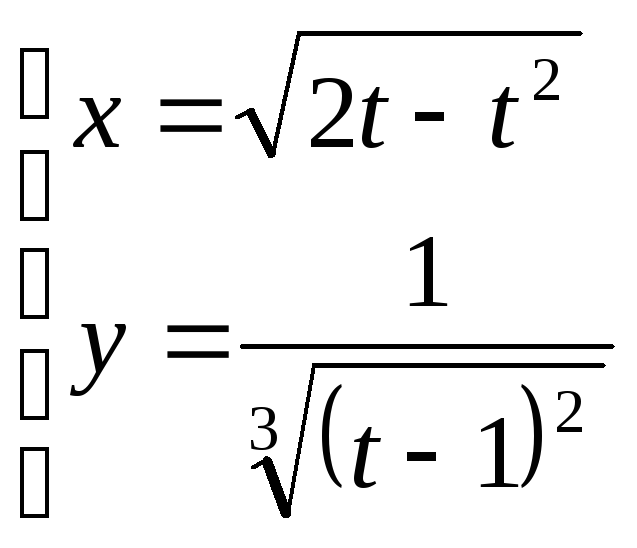 ;
;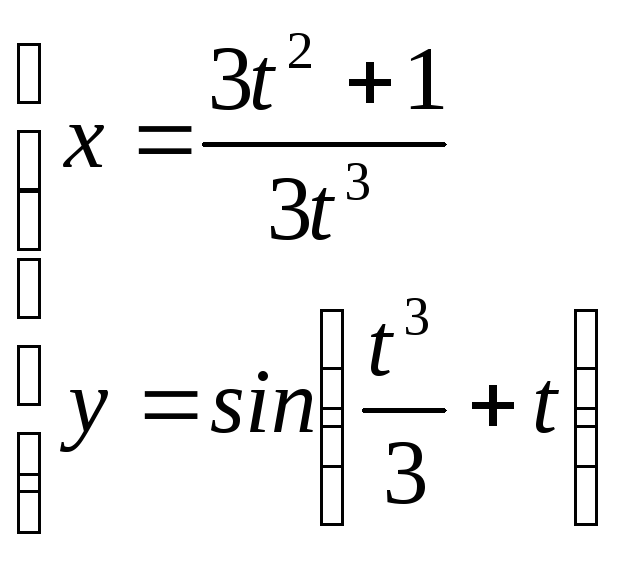 .
.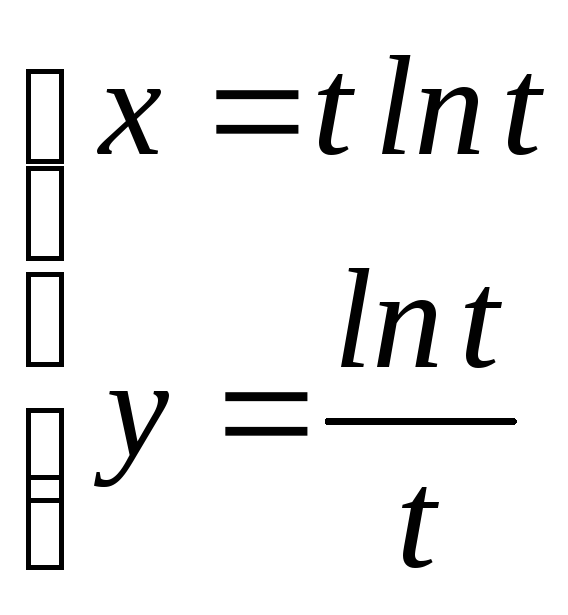 ,
t=1;
,
t=1; ,
,
 ;
; ;
; ;
;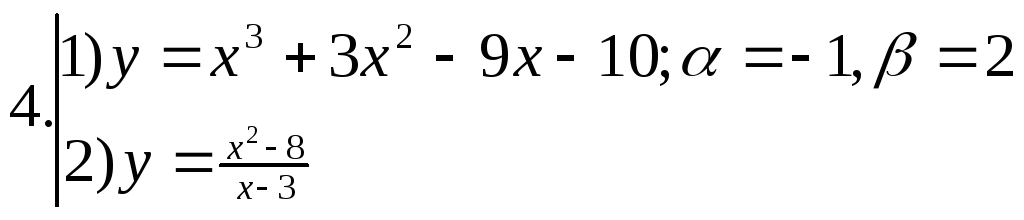 ;
;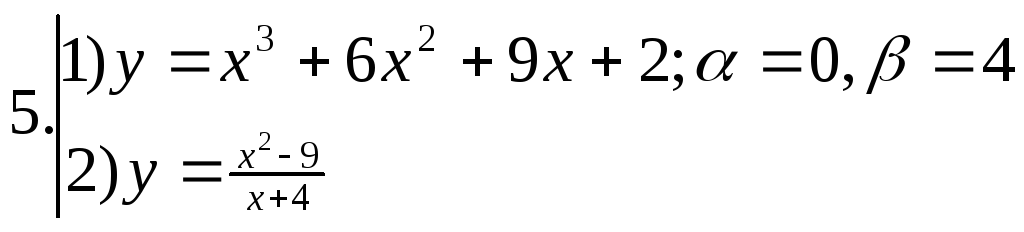 ;
; ;
; ;
;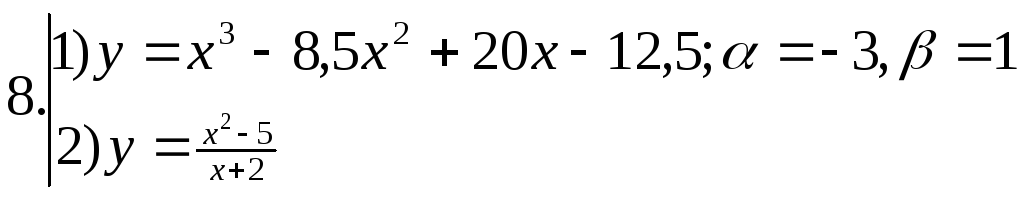 ;
;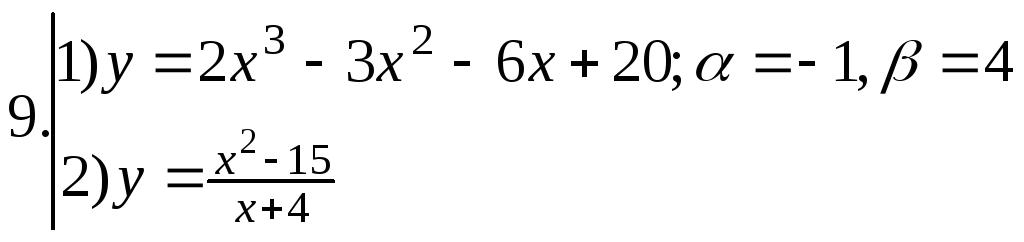 ;
; ;
; ;
; ;
;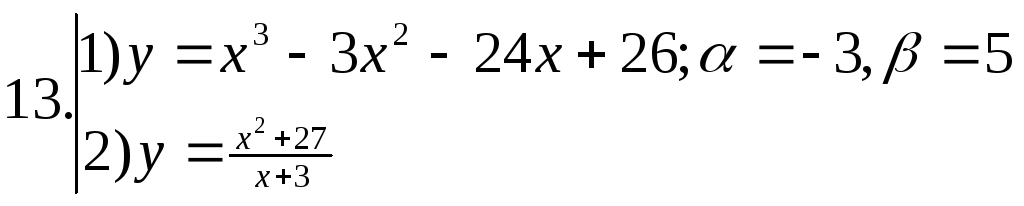 ;
; ;
; ;
; ;
;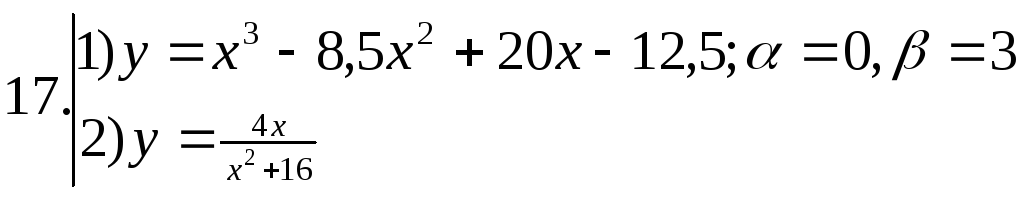 ;
; ;
;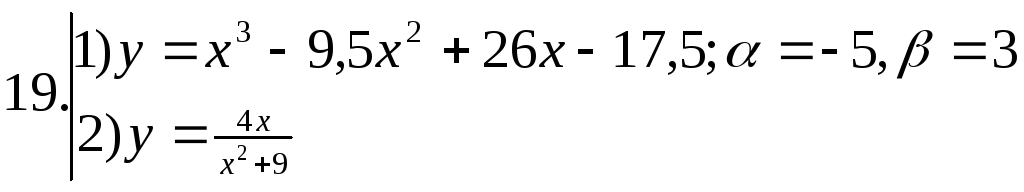 ;
; ;
;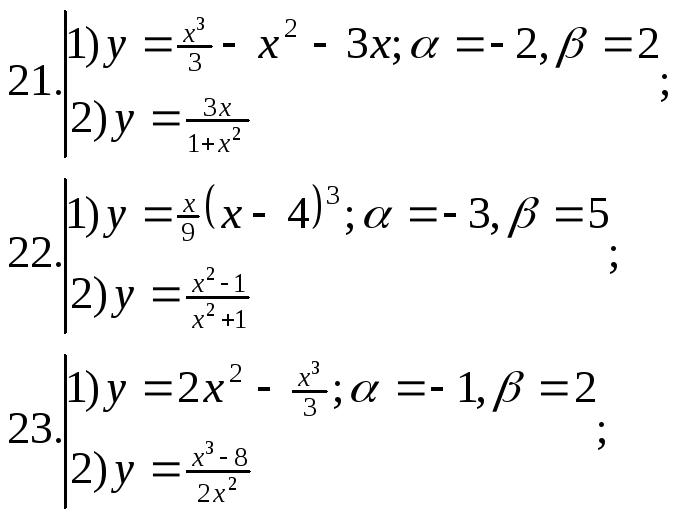
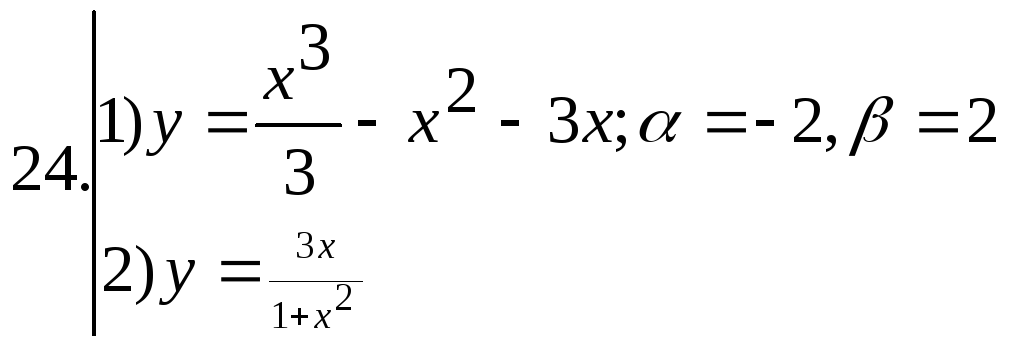 ;
; ;
; ;
;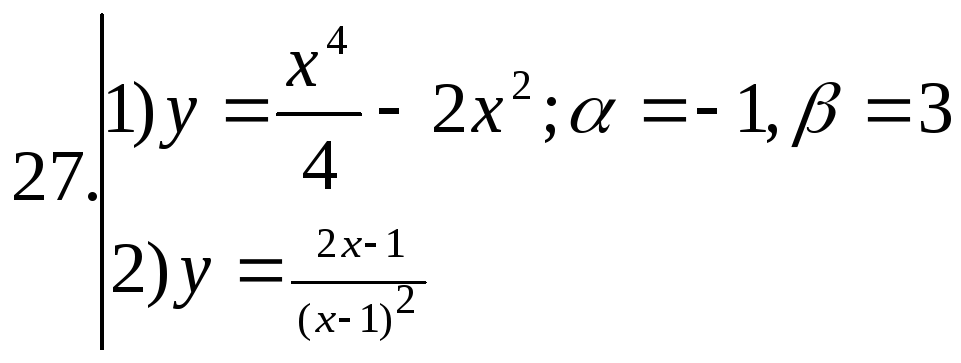 ;
;
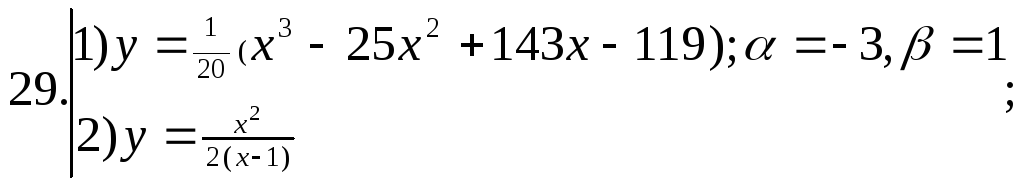
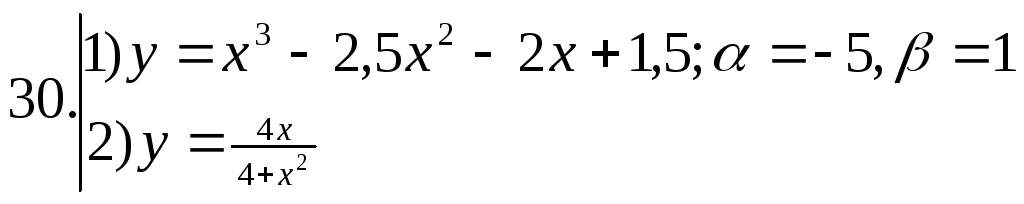 .
.