
- •Тест на проверку выживаемости знаний за 1 курс Тема 1. Математический анализ
- •Множество значений, которые может принимать переменная величина х в данном соответствии
- •Множество значений, которые может принимать переменная величина y в данном соответствии*
- •Множество значений переменной величины х, которые берутся при нахождении переменной величины y
- •Значение функции в этой точке равно нулю
- •Главная часть приращения функции
- •Приращение аргумента
- •Функция, которая превращает данное уравнение в тождество при данных начальных условиях *
- •Множество функций, каждая из которых превращает данное уравнение в тождество
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Элементы векторной алгебры
- •Тема 4. Аналитическая геометрия на плоскости
Тема 3. Элементы векторной алгебры
-
Модулем вектора называется
-
длина вектора*
-
вектор единичной длины
-
вектор, начало и конец которого совпадают
-
-
Векторы, расположенные на параллельных прямых или на одной прямой называются
-
коллинеарными*
-
сонаправленными
-
противоположно направленными
-
равными
-
противоположными
-
-
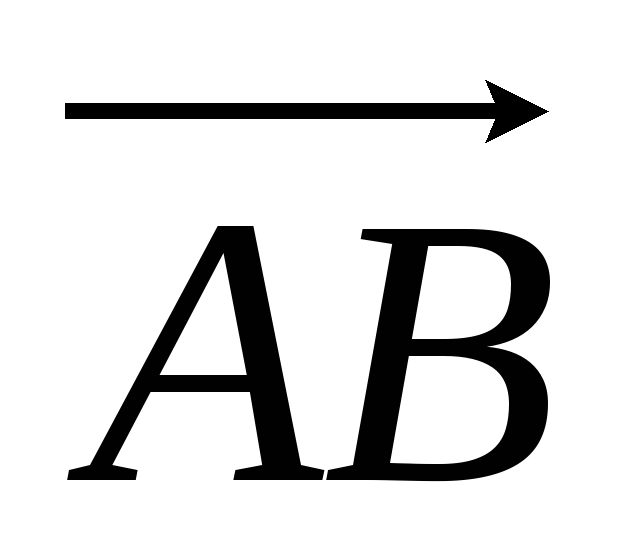
Даны координаты точек на плоскости А(х1;у1) и В(х2;у2). Координаты соответствующего вектора
 определяются
по формуле:
А)
определяются
по формуле:
А)
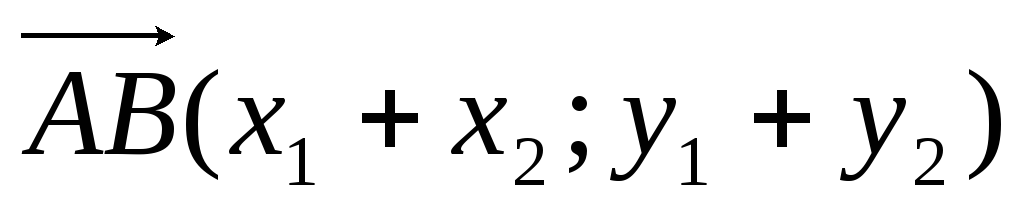 ;
Б)
;
Б)
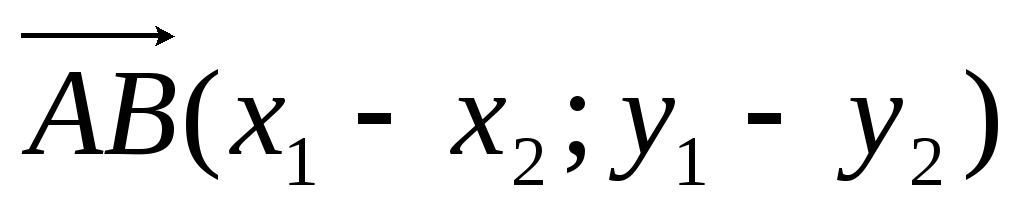 ;
В)
;
В)

-
А
-
Б
-
В*
-
-
Дан вектор
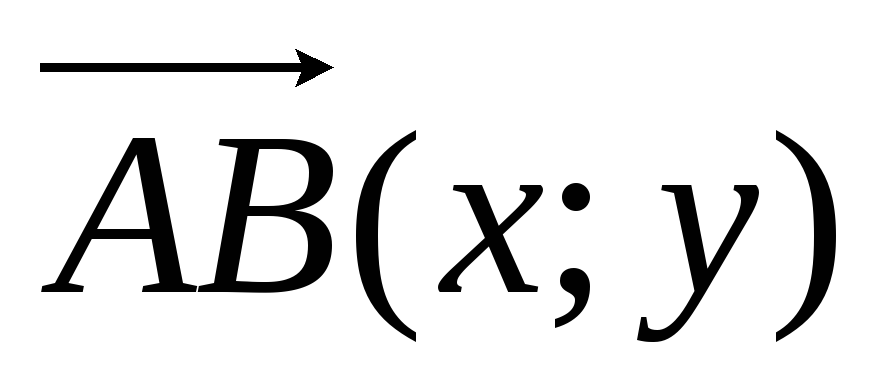 .
Его модуль можно найти из соотношения:
А)
.
Его модуль можно найти из соотношения:
А)
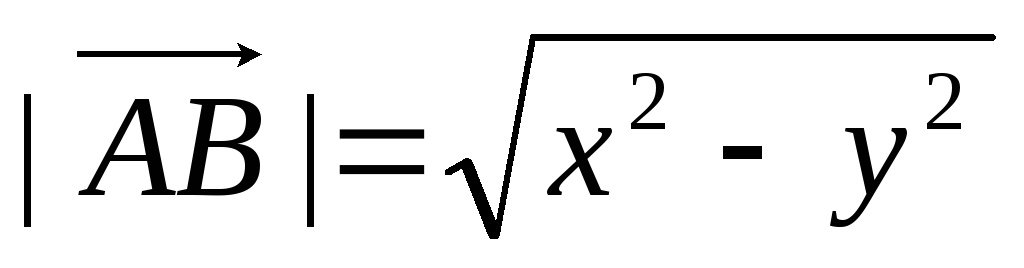 ;
Б)
;
Б)
 ;
В)
;
В)
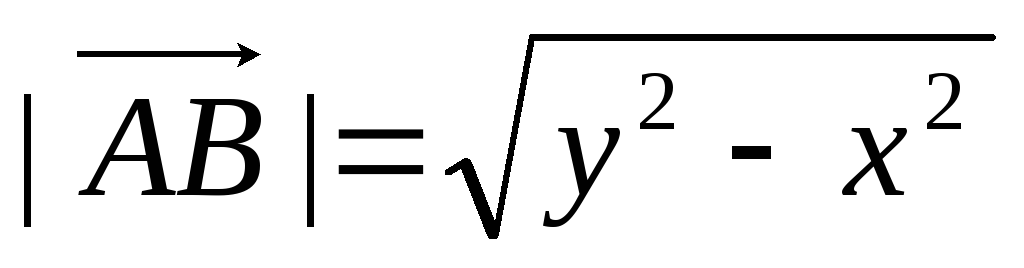
-
А
-
Б *
-
В
-
-
Векторы
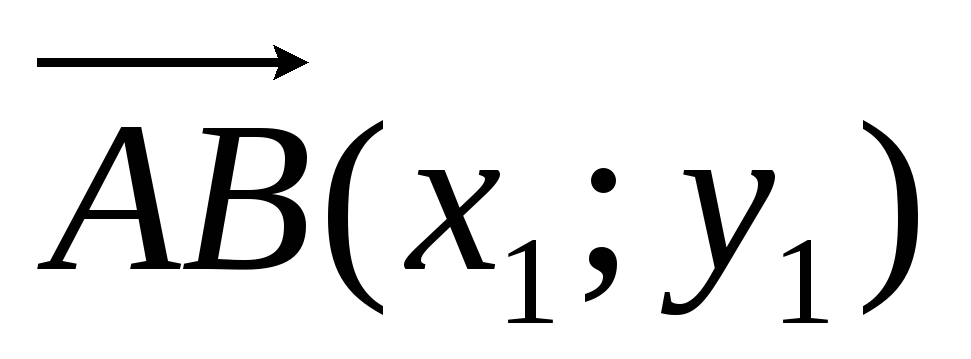 и
и
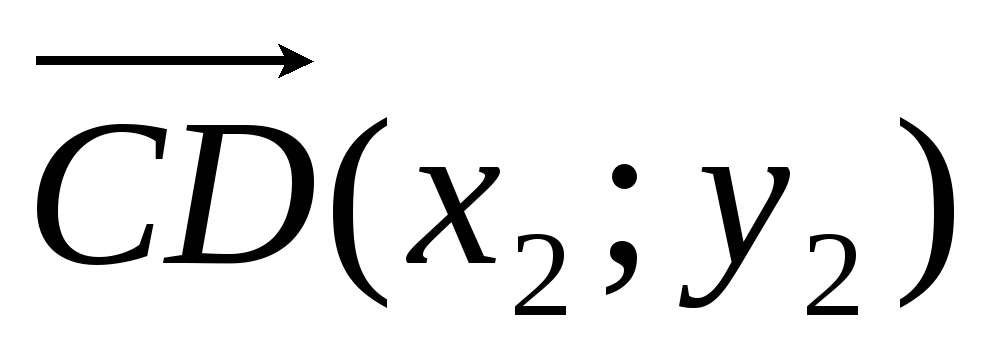 коллинеарные
тогда и только тогда, когда выполняется
соотношение для их координат:
А)
коллинеарные
тогда и только тогда, когда выполняется
соотношение для их координат:
А)
 ;
Б)
;
Б)
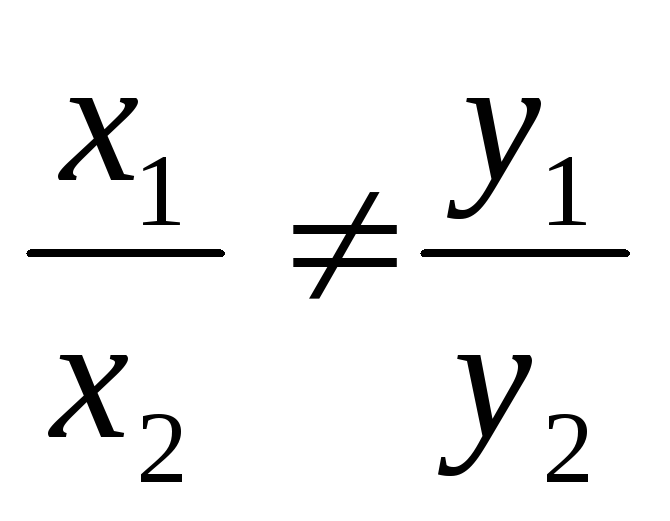 ;
В)
;
В)
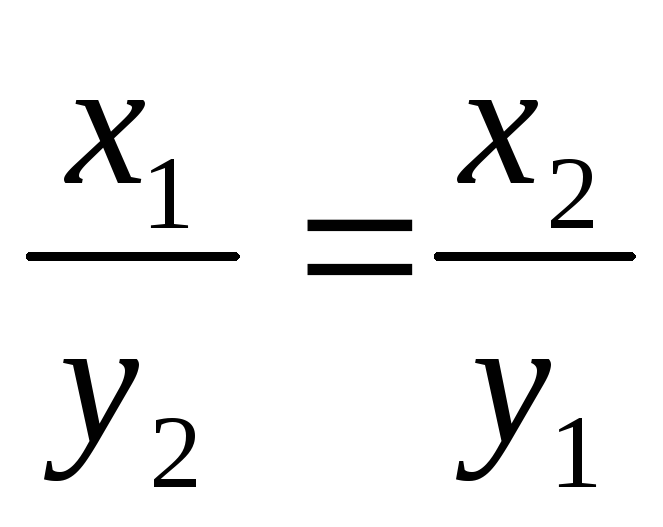
-
А*
-
Б
-
В
-
-
Скалярное произведение для векторов
 и
и
 в
координатной форме равно:
А)
в
координатной форме равно:
А)
 ;
Б)
;
Б) ;
В)
;
В)
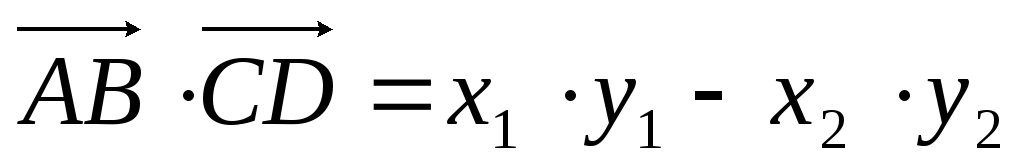
-
А
-
Б *
-
В
-
-
Даны вектора. Их скалярное произведение векторов
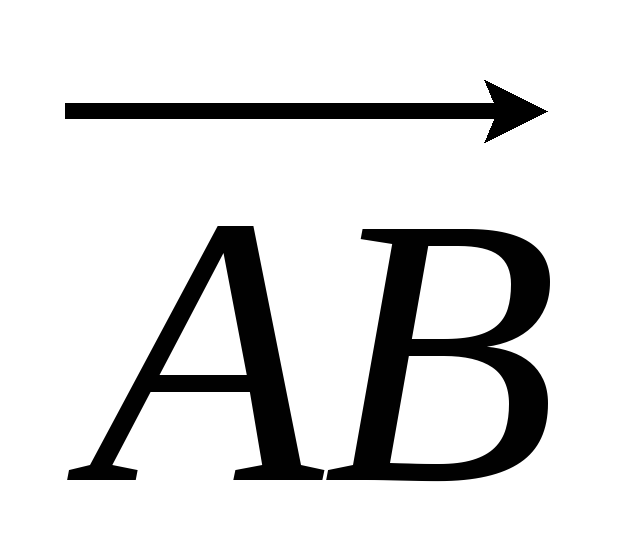 и
и
 по определению равно:
А)
по определению равно:
А)
 ;
Б)
;
Б)
 ;
В)
;
В)

-
А*
-
Б
-
В
-
-
Критерий перпендикулярности ненулевых векторов
-
перпендикулярны тогда и только тогда, когда их скалярное произведение равно 0*
-
перпендикулярны тогда и только тогда, когда их скалярное произведение не равно 0
-
перпендикулярны тогда и только тогда, когда их векторное произведение равно 0
-
перпендикулярны тогда и только тогда, когда их векторное произведение не равно 0
-
-
Если
 ||
||
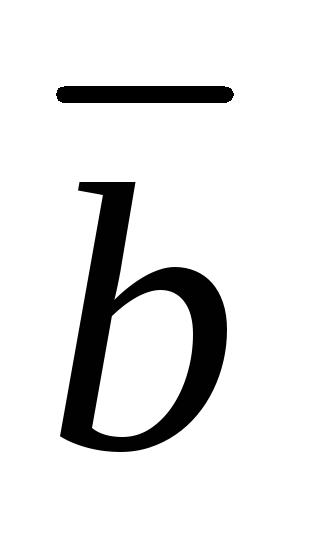 ,
то: А)
,
то: А)
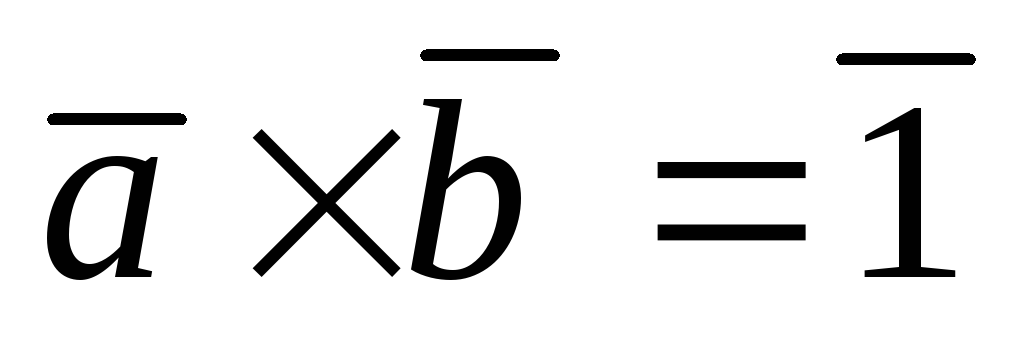 ;
Б)
;
Б)
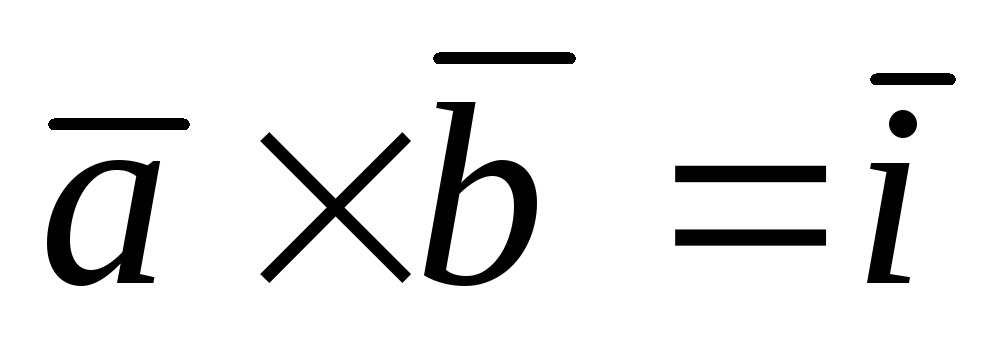 ;
В)
;
В)

-
А
-
Б
-
В *
-
-
Смешанное произведение векторов (
 ×
×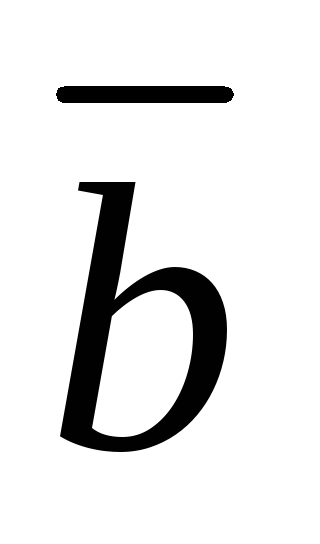 )
)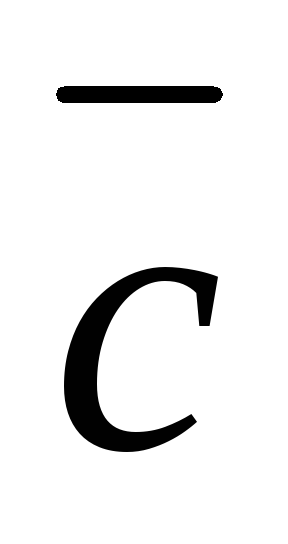 в координатной форме равно определителю
третьего порядка, составленному из
координат перемножаемых векторов по
правилу:
в координатной форме равно определителю
третьего порядка, составленному из
координат перемножаемых векторов по
правилу:
А)
 ;
Б)
;
Б)
 ;
В)
;
В)
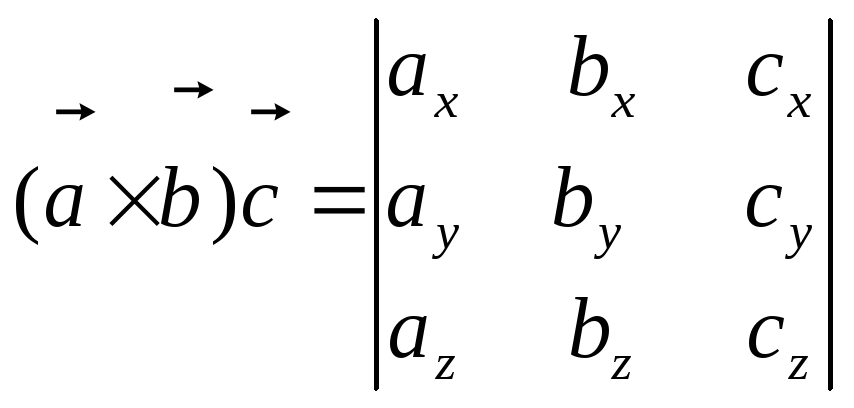
-
А *
-
Б
-
В
Тема 4. Аналитическая геометрия на плоскости
-
Расстояние между любыми двумя точками плоскости можно определить по формуле: А)
 ;
Б)
;
Б)
 ;
В)
;
В)

-
А
-
Б *
-
В
-
Координаты середины отрезка между двумя точками на плоскости: А)
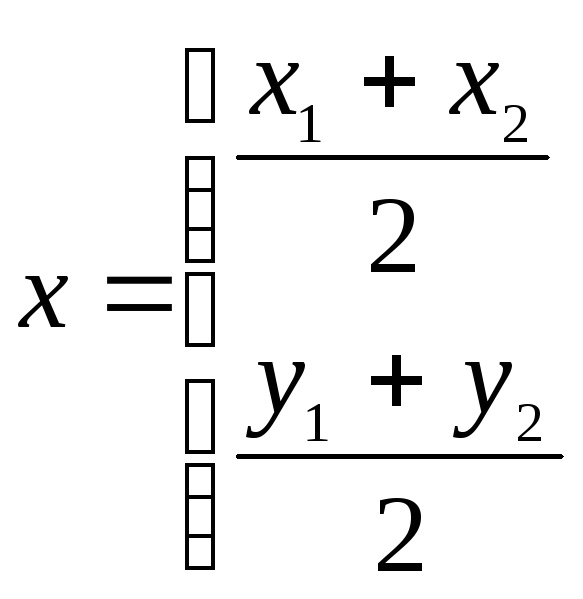 ;
Б)
;
Б)
 ;
В)
;
В)
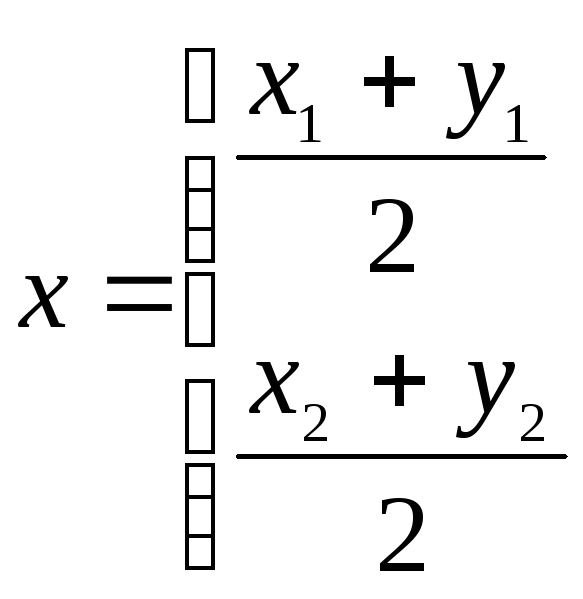
-
А *
-
Б
-
В
-
Уравнение прямой в отрезках записывается следующим образом:
А)
![]() ;
Б)
;
Б)
![]() ;
В)
;
В)
![]()
-
А
-
Б
-
В *
-
Уравнение прямой с угловым коэффициентом записывается следующим образом: А)
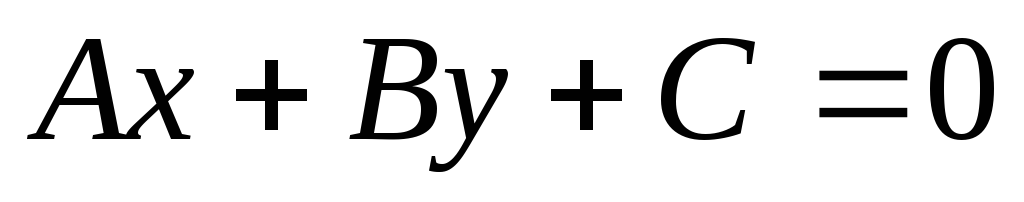 ;
Б)
;
Б)
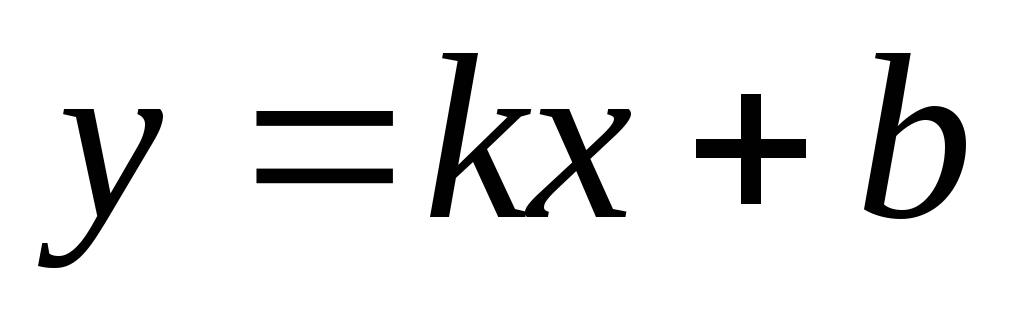 ;
В)
;
В)

-
А
-
Б *
-
В
-
Две прямые
 и
и
 будут взаимно перпендикулярны, если
произведение
будут взаимно перпендикулярны, если
произведение
 равно
равно
-
1
-
-1 *
-
0
-
Две прямые
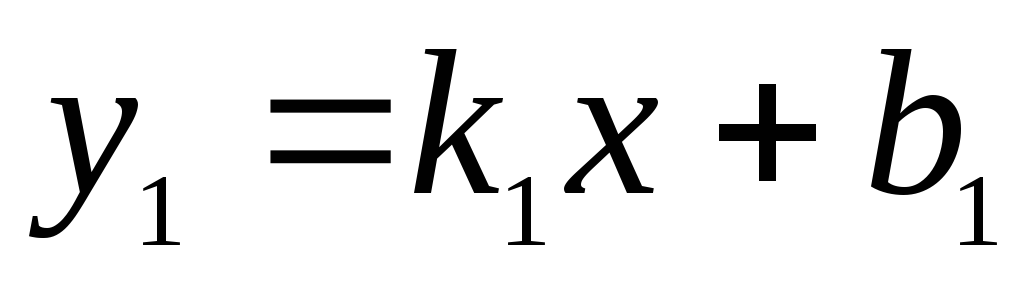 и
и
 будут взаимно параллельны, если
будут взаимно параллельны, если
-
Произведение угловых коэффициентов равно 1
-
Произведение угловых коэффициентов равно -1
-
Угловые коэффициенты равны *
-
Уравнение окружности имеет вид: А)
 ;
Б)
;
Б)
 ;
В)
;
В)
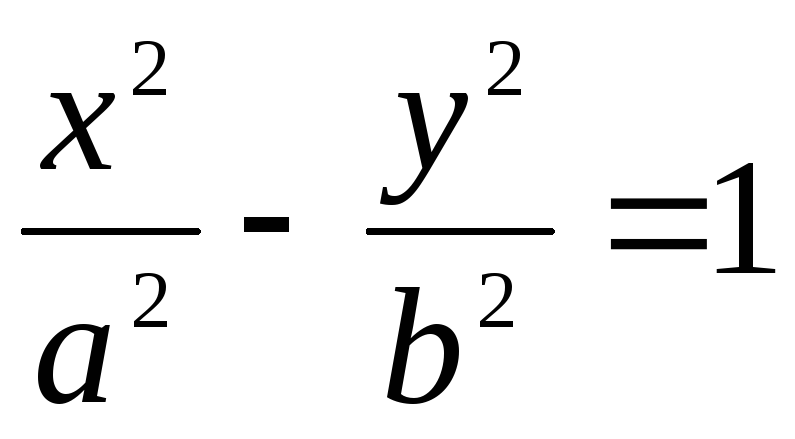 ;
Г)
;
Г)

-
А
-
Б *
-
В
-
Г
-
Уравнение гиперболы имеет вид: А)
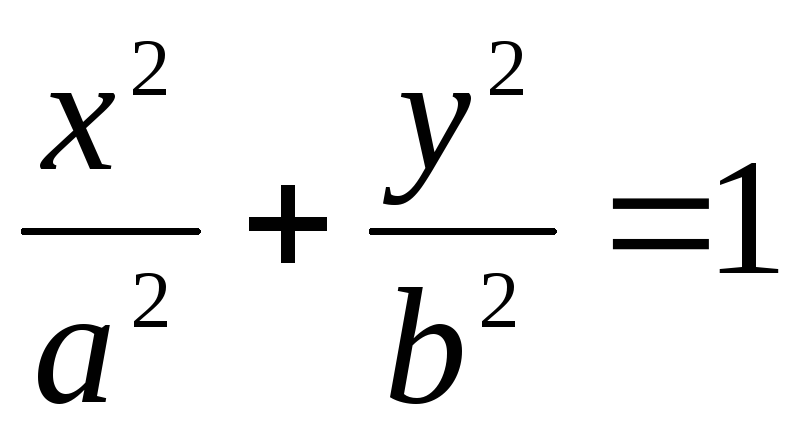 ;
Б)
;
Б)
 ;
В)
;
В)
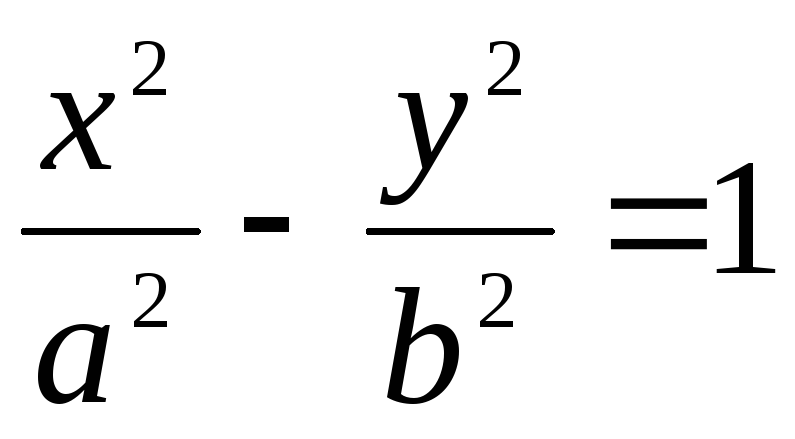 ;
Г)
;
Г)

-
А
-
Б
-
В *
-
Г
-
Уравнение эллипса имеет вид: А)
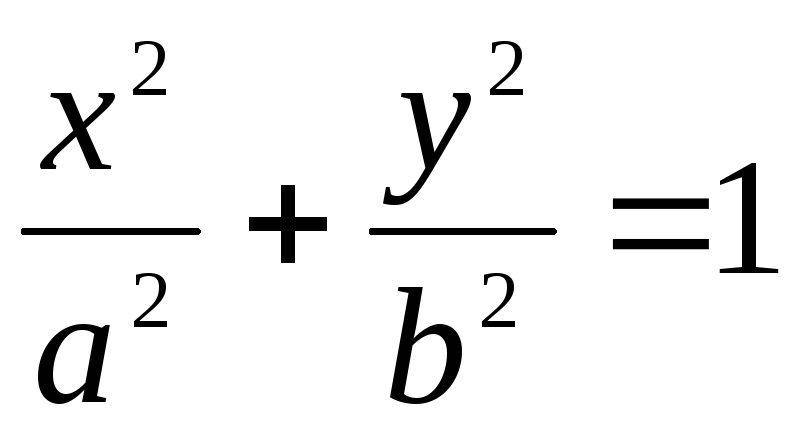 ;
Б)
;
Б)
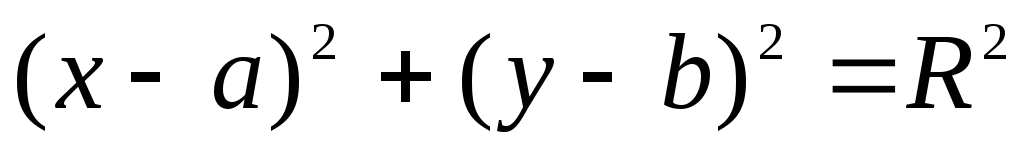 ;
В)
;
В)
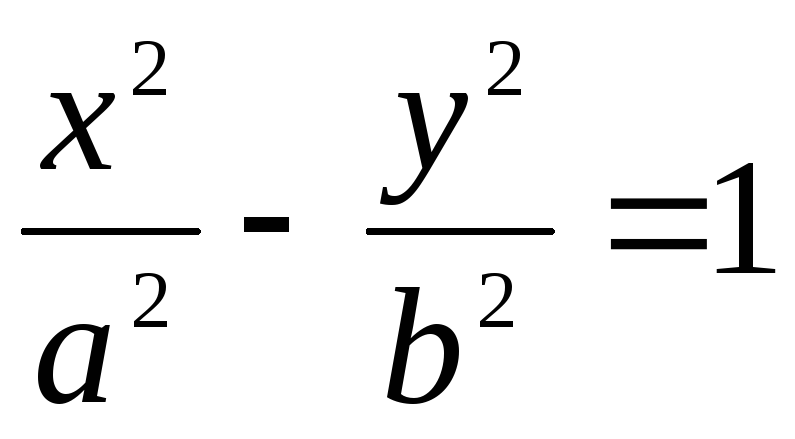 ;
Г)
;
Г)
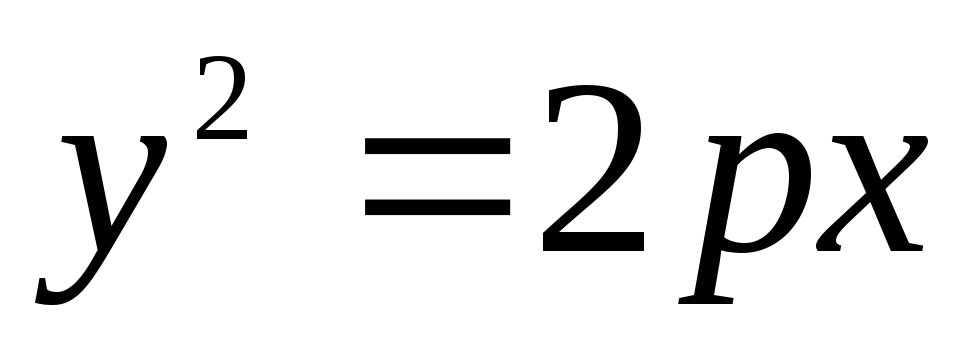
-
А *
-
Б
-
В
-
Г
-
Уравнение параболы имеет вид: А)
 ;
Б)
;
Б)
 ;
В)
;
В)
 ;
Г)
;
Г)

-
А
-
Б
-
В
-
Г *
