
- •Тест на проверку выживаемости знаний за 1 курс Тема 1. Математический анализ
- •Множество значений, которые может принимать переменная величина х в данном соответствии
- •Множество значений, которые может принимать переменная величина y в данном соответствии*
- •Множество значений переменной величины х, которые берутся при нахождении переменной величины y
- •Значение функции в этой точке равно нулю
- •Главная часть приращения функции
- •Приращение аргумента
- •Функция, которая превращает данное уравнение в тождество при данных начальных условиях *
- •Множество функций, каждая из которых превращает данное уравнение в тождество
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Элементы векторной алгебры
- •Тема 4. Аналитическая геометрия на плоскости
Тест на проверку выживаемости знаний за 1 курс Тема 1. Математический анализ
-
Функцией Y = f(x) называется
-
множество значений переменной величины y, вычисленных при подстановке значений переменной величины x в cоответствующую формулу
-
соответствие, по которому для любого определенного значения переменной величины х можно вычислить единственное значение переменной величины y*
-
соответствие, по которому для любого определенного значения переменной величины y можно вычислить единственное значение переменной величины x
-
Областью определения функции Y = f(x) называется
-
множество значений, которые может принимать переменная величина х в данном соответствии*
-
множество значений, которые может принимать переменная величина Y в данном соответствии
-
множество значений переменной величины х, которые берутся при нахождении переменной величины Y
-
Множеством значений функции Y = f(x) называется
-
Множество значений, которые может принимать переменная величина х в данном соответствии
-
Множество значений, которые может принимать переменная величина y в данном соответствии*
-
Множество значений переменной величины х, которые берутся при нахождении переменной величины y
-
Область определения функции
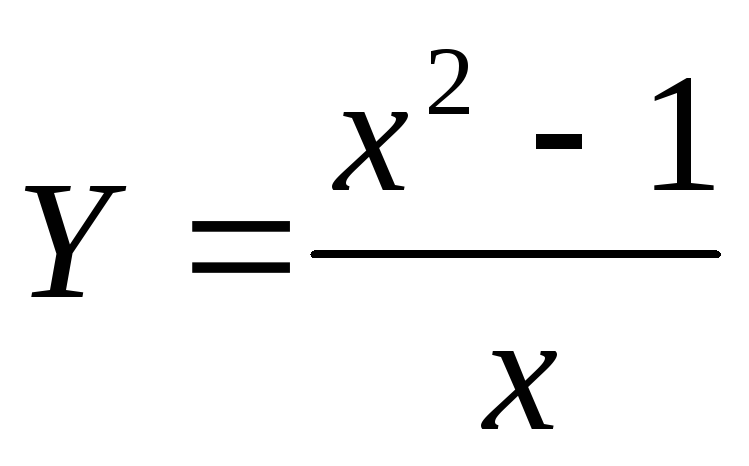 задается
выражением:
А) х
(- ; 0)
(0; +); Б) х
(- ; 0)
(0; +); В) х
(- ; 0)
(0; 1) (1; +)
задается
выражением:
А) х
(- ; 0)
(0; +); Б) х
(- ; 0)
(0; +); В) х
(- ; 0)
(0; 1) (1; +)
-
А*
-
Б
-
В
-
Функция называется непрерывной на промежутке (a; b) если
-
Аргумент этой функции может принимать любые значения из этого промежутка*
-
Функции может принимать любые значения из этого промежутка
-
Производная непрерывной Y’ функции Y = f(x) задается равенством: А)
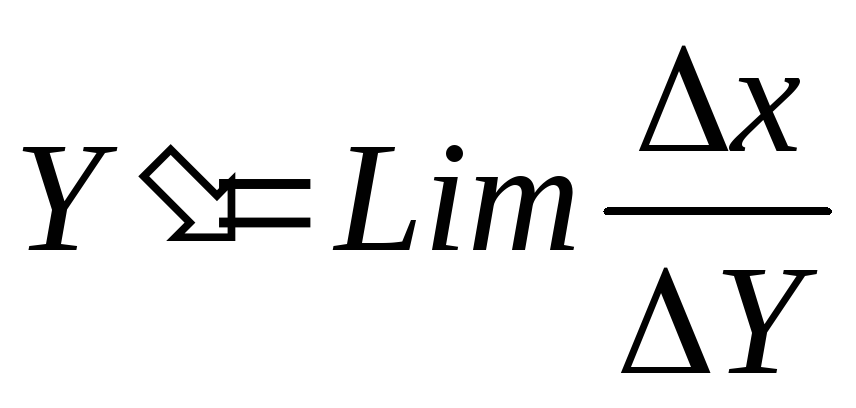 при
при
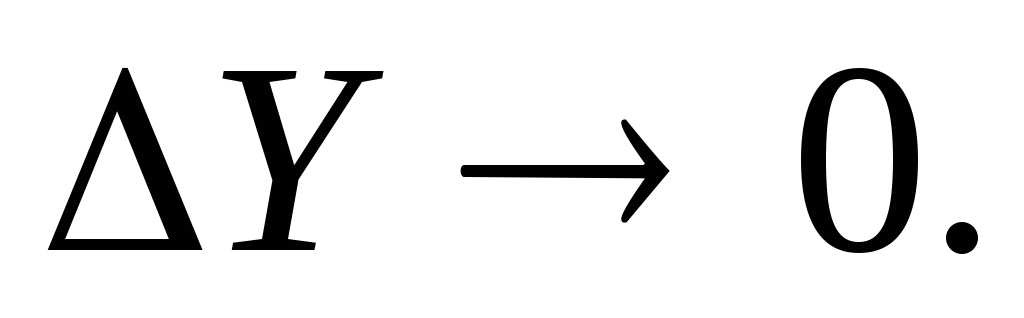 Б)
Б)
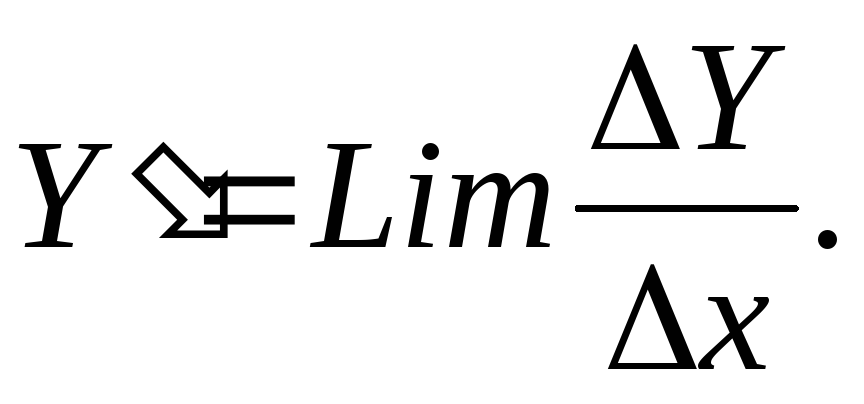 при
при
 В)
В)
 при
при

-
А
-
Б *
-
В
-
Второй производной или производной второго порядка Y функции Y = f(x) называется
-
Производная от производной функции *
-
Квадрат ее производной 2
-
Производная от степенной функции второго порядка
-
Производная функции
 равна: А ) Y
= 2x2 ;
Б) Y
= 3x4; В)
Y
=6х3
равна: А ) Y
= 2x2 ;
Б) Y
= 3x4; В)
Y
=6х3
-
А *
-
Б
-
В
-
-
Дифференциал функции – это
-
главная часть приращения функции *
-
приращение аргумента
-
первообразная функции
-
Геометрический смысл первой производной
-
Угловой коэффициент касательной к графику функции *
-
Приращение аргумента
-
Скорость изменения функции
-
Механический смысл первой производной
-
Угловой коэффициент касательной к графику функции
-
Приращение функции
-
Скорость изменения функции *
-
Механический смысл второй производной
-
Угловой коэффициент касательной к графику функции
-
Приращение функции
-
Скорость изменения скорости (ускорение) функции *
-
Если функция возрастает на интервале, то на этом интервале
-
Производная функции равна нулю
-
Производная функции больше нуля *
-
Производная функции меньше нуля
-
Если функция убывает на интервале, то на этом интервале
-
Производная функции равна нулю
-
Производная функции больше нуля
-
Производная функции меньше нуля *
-
Если график функции является выпуклым на интервале, то на этом интервале
-
Вторая производная функции равна нулю
-
Вторая производная функции больше нуля
-
Вторая производная функции меньше нуля *
