
Лабораторна робота № 2
Графічний метод розв’язання задач
лінійного програмування
2.1. Мета роботи – ознайомлення з принципами побудови математичної моделі задачі про оптимальне використання сировини; дослідження особливостей застосування графічного методу для визначення опорного плану задачі лінійного програмування та аналізу його стійкості щодо ринкової ціни на одиницю продукції.
2.2. Змістовна постановка задачі та її математична модель
Не порушуючи спільності, розглянемо задачу лінійного програмування у стандартній формі. Це передбачає, що основна система обмежень надана у вигляді нерівностей одного знака і знак нерівностей відповідає виду екстремуму цільової функції. Зрозуміло, що геометрична інтерпретація доцільна, якщо многокутник планів належить до двовимірного простору. У випадку трьох вимірів задача значно ускладнюється, а для чотирьох вимірів графічне розв’язання стає неможливим. Отже, математичну модель задачі будемо розглядати у вигляді:
![]() (2.1)
(2.1)
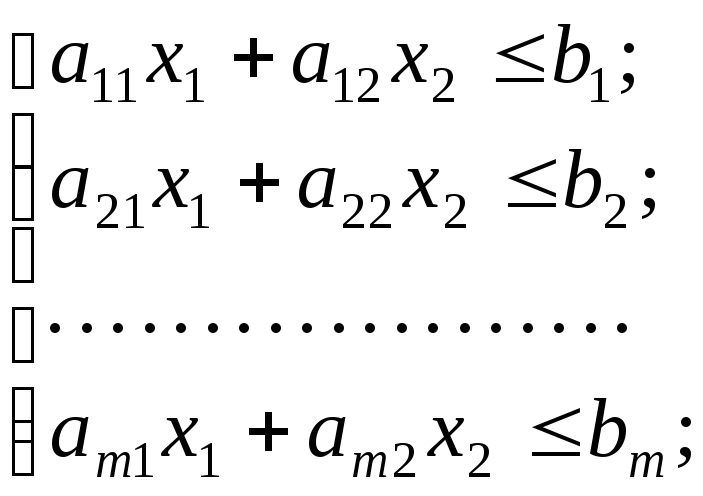 (2.2)
(2.2)
![]() .
(2.3)
.
(2.3)
Кожна
нерівність основної
системи обмежень
(2.2) згідно з рівнянням прямої
![]() поділяє площину 0Х1Х2
на півплощини та визначає ту з півплощин,
де нерівність виконується. Обмеження
на
знак
(2.3) також визначають півплощини, які
обмежені прямими:
поділяє площину 0Х1Х2
на півплощини та визначає ту з півплощин,
де нерівність виконується. Обмеження
на
знак
(2.3) також визначають півплощини, які
обмежені прямими:
![]() та
та
![]() ,
отже, область визначення даної задачі
розташована у I-й чверті координатної
площини. Якщо система обмежень сумісна,
то півплощини, де виконуються нерівності
системи обмежень, перетинаючись,
утворюють многокутник
можливих розв’язків
задачі лінійного програмування, тобто
многокутник
планів.
,
отже, область визначення даної задачі
розташована у I-й чверті координатної
площини. Якщо система обмежень сумісна,
то півплощини, де виконуються нерівності
системи обмежень, перетинаючись,
утворюють многокутник
можливих розв’язків
задачі лінійного програмування, тобто
многокутник
планів.
Оскільки
у випадку застосування графічного
способу розв’язання цільова функція
повинна бути функцією двох змінних,
графіком її у тривимірному просторі
буде деяка площина. На площині 0Х1Х2
цільова функція відображається за
допомогою ліній
рівня,
тобто ліній, що відповідають певному
сталому значенню цільової функції
![]() .
Так, лінія рівня, для якої значення
цільової функції дорівнює нулю, описується
рівнянням
.
Так, лінія рівня, для якої значення
цільової функції дорівнює нулю, описується
рівнянням
![]() ,
і графіком цієї лінії рівня є пряма, що
проходить через початок координат.
Коефіцієнти цільової функції мають
значення проекцій нормалі до лінії
рівня:
,
і графіком цієї лінії рівня є пряма, що
проходить через початок координат.
Коефіцієнти цільової функції мають
значення проекцій нормалі до лінії
рівня:
![]() .
Градієнт,
тобто вектор, що вказує напрямок найбільш
швидкого зростання функції, визначаємо
за вектором нормалі:
.
Градієнт,
тобто вектор, що вказує напрямок найбільш
швидкого зростання функції, визначаємо
за вектором нормалі:
![]() . (2.4)
. (2.4)
Відповідно, значення цільової функції зростатиме, якщо лінію рівня пересувати в напряму нормалі.
До речі, аналогічну графічну інтерпретацію може мати задача лінійного програмування і для більшої кількості керованих змінних, якщо різниця між кількістю змінних та кількістю рівнянь основної системи обмежень дорівнює двом.
Графічний розв’язок задачі лінійного програмування базується на трьох теоремах, які наводимо без доведення.
Теорема 2.1. Множина планів задачі лінійного програмування є опуклою, тобто всі внутрішні точки відрізку, що з’єднує довільні точки многокутника, теж належать цьому многокутнику.
Теорема 2.2. Кожній вершині многокутника планів відповідає опорний план і кожному опорному плану відповідає вершина многокутника планів.
Теорема 2.3. Екстремум цільової функції відповідає вершині многокутника планів.
2.3. Завдання
Технологія,
що застосовується на малому підприємстві,
дозволяє виготовляти керамічну плитку
двох типів: для внутрішніх та зовнішніх
робіт. Для виробництва кожного з типів
керамічної плитки використовується
чотири види сировини. Кількість кожної
виду сировини, що витрачається на
виготовлення однієї партії виробу
залежно від типу продукції, задана
матрицею технологічних коефіцієнтів
![]() :
:
 ,
,
рядки якої відповідають певному виду сировини, а стовпці – певному виді продукції, що виробляється. Запаси сировини на підприємстві визначаються матрицею-стовпцем
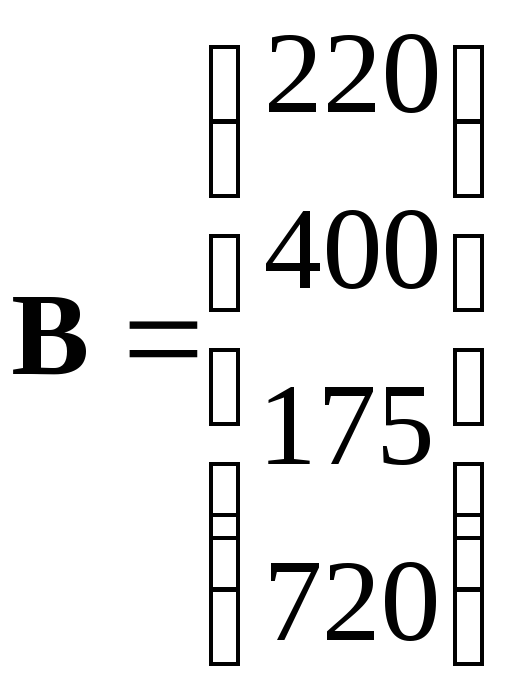 .
.
На
даний момент часу ринкові ціни на кожний
вид продукції описуються матрицею-рядком
![]() .
.
Необхідно визначити, у якій кількості слід виробляти продукцію кожного виду, щоб загальний прибуток від її реалізації був би найбільшим.
2.4. Приклад виконання лабораторної роботи № 3
Побудуємо
математичну модель задачі. Матриця
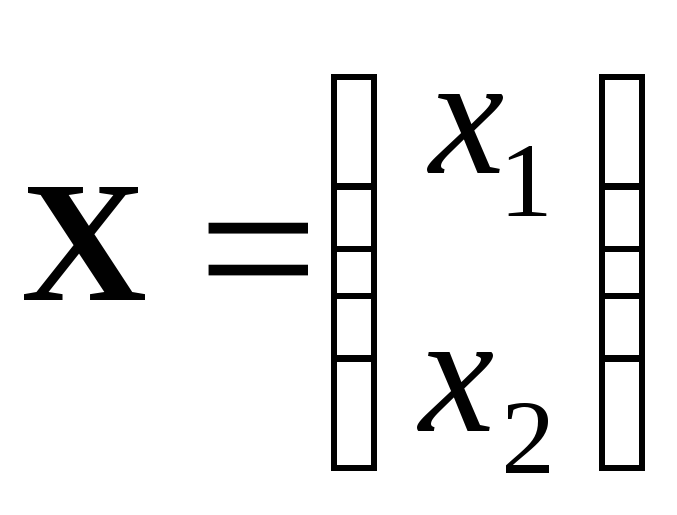 описує можливі плани виробництва, де
кількість продукції 1-го типу позначається
описує можливі плани виробництва, де
кількість продукції 1-го типу позначається
![]() ,
а кількість продукції 2-го типу –
,
а кількість продукції 2-го типу –
![]() .
Відповідно
.
Відповідно
![]() .
(2.3І)
.
(2.3І)
Отже, маємо обмеження на знак.
Витрати сировини всіх видів на виготовлення продукції обох типів можна записати у вигляді нерівностей:
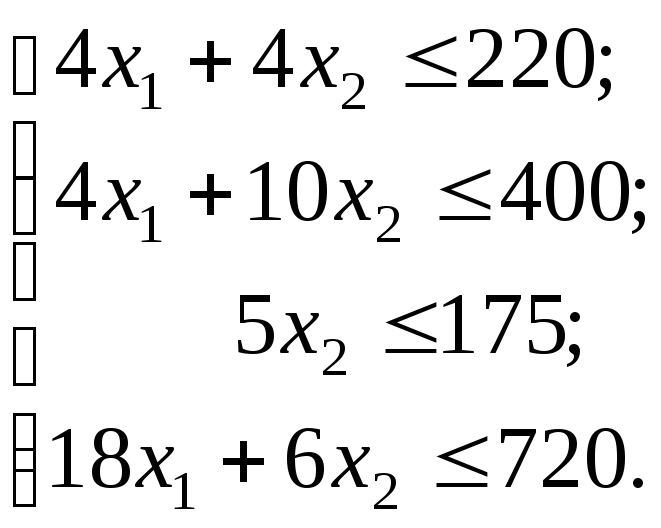 (2.2І)
(2.2І)
Це основна система обмежень, яка разом з обмеженнями на знак визначає множину можливих планів виробництва.
Сукупність нерівностей (2.2І) та (2.3І) визначає множину можливих планів виробництва. Серед них оптимальним планом є той, що забезпечує найбільший прибуток від реалізації продукції. Відповідно критерієм ефективності є функція, що характеризує загальний прибуток від реалізації при заданому рівні ринкових цін на продукцію:
![]() .
(2.1І)
.
(2.1І)
Співвідношення
(2.1І)
– (2.3І)
утворюють математичну модель задачі
про оптимальне використання сировини.
Отже, цільова функція і всі функції
системи обмежень є лінійними, тобто
маємо задачу лінійного програмування.
Оскільки цільова функція цієї задачі
досліджується на максимум і всі нерівності
основної системи обмежень мають знак
![]() ,
то математична модель задачі лінійного
програмування надана у стандартній
формі. Задача має лише дві змінні, отже,
її можна розв’язати
за допомогою
графічного
методу.
,
то математична модель задачі лінійного
програмування надана у стандартній
формі. Задача має лише дві змінні, отже,
її можна розв’язати
за допомогою
графічного
методу.
Розв’язання задачі лінійного програмування про оптимальне використання сировини з використанням графічного методу будемо здійснювати за таким алгоритмом.
1.
За основною системою обмежень та
обмеженнями за знаком будуємо многокутник
планів, тобто знаходимо область значень
змінних
![]() та
та
![]() .
Для цього за кожною нерівністю основної
системи обмежень знайдемо на площині
0Х1Х2
область
її виконання. Наприклад, визначимо
півплощину, де виконується нерівність
.
Для цього за кожною нерівністю основної
системи обмежень знайдемо на площині
0Х1Х2
область
її виконання. Наприклад, визначимо
півплощину, де виконується нерівність
![]() .
З цією метою перепишемо це обмеження у
вигляді рівняння і перетворимо рівняння
прямої до вигляду у відрізках на осях,
поділивши обидві його частини на 220.
Матимемо:
.
З цією метою перепишемо це обмеження у
вигляді рівняння і перетворимо рівняння
прямої до вигляду у відрізках на осях,
поділивши обидві його частини на 220.
Матимемо:
![]()
![]() .
.
Це
означає, що пряма
![]() відсікає на осі 0Х1
відрізок 55 (знаменник першого дробу в
рівнянні прямої) та на осі 0Х2
– теж відрізок 55 (знаменник другого
дробу). Відклавши ці відрізки вздовж
відповідних осей, побудуємо цю пряму
(рис. 2.1). Щоб визначити півплощину, де
виконується вихідна нерівність,
підставимо в цю нерівність координати
точки, що не належить прямій
відсікає на осі 0Х1
відрізок 55 (знаменник першого дробу в
рівнянні прямої) та на осі 0Х2
– теж відрізок 55 (знаменник другого
дробу). Відклавши ці відрізки вздовж
відповідних осей, побудуємо цю пряму
(рис. 2.1). Щоб визначити півплощину, де
виконується вихідна нерівність,
підставимо в цю нерівність координати
точки, що не належить прямій
![]() ,
наприклад, початок координат. Так, для
т. О (0; 0)
маємо:
,
наприклад, початок координат. Так, для
т. О (0; 0)
маємо:
![]() .
Оскільки отримали правильну числову
нерівність, то т. О
належить тій півплощині, де вихідна
нерівність задовольняється. Отже,
перпендикулярно до лінії
.
Оскільки отримали правильну числову
нерівність, то т. О
належить тій півплощині, де вихідна
нерівність задовольняється. Отже,
перпендикулярно до лінії
![]() ставимо дві стрілки, які вказують
півплощину, де ця нерівність виконується.
ставимо дві стрілки, які вказують
півплощину, де ця нерівність виконується.
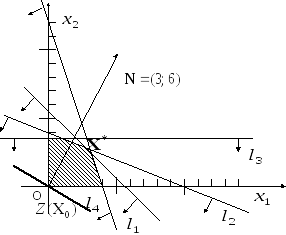
Рис. 2.1. Графічний розв’язок
Пронумеруємо всі нерівності основної системи обмежень і для кожної з них визначимо півплощину, де це обмеження виконується. Як наслідок отримаємо область, усі точки якої задовольняють як основній системі обмежень, так і обмеженням на знак. Це і є многокутник планів задачі лінійного програмування. На рис. 3.1 його виділили штриховкою.
2.
За коефіцієнтами рівняння цільової
функції знаходимо вектор нормалі
![]() і перпендикулярно до нього через початок
координат проводимо лінію рівня
і перпендикулярно до нього через початок
координат проводимо лінію рівня
![]() ,
що відповідає нульовим значенням
невідомих. У даному випадку лінія рівня
входить до многокутника планів через
т. О, якій відповідає опорний план
,
що відповідає нульовим значенням
невідомих. У даному випадку лінія рівня
входить до многокутника планів через
т. О, якій відповідає опорний план
![]() .
За цим планом цільова функція має
найменше з можливих значень:
.
За цим планом цільова функція має
найменше з можливих значень:
![]() .
.
Оскільки
цільова функція досліджується на
максимум, то пересуваючи лінію рівня в
напрямку вектора нормалі, визначаємо
вершину многокутника планів
![]() ,
через яку функція
,
через яку функція
![]() виходить з многокутника планів (див.
рис. 2.1).
Ця точка відповідає оптимальному плану,
за яким цільова функція має максимум:
виходить з многокутника планів (див.
рис. 2.1).
Ця точка відповідає оптимальному плану,
за яким цільова функція має максимум:
![]() .
.
3.
Визначаємо лінії, перетин яких утворює
вершину
![]() ,
якій відповідає максимальне значення
цільової функції. Це лінії
,
якій відповідає максимальне значення
цільової функції. Це лінії
![]() та
та
![]() .
Отже, оптимальному плану
.
Отже, оптимальному плану
![]() відповідає повне використання сировини
першого і другого видів, що означає, що
відповідні цим видам сировини нерівності
основної системи обмежень перетворились
на рівняння. Утворюємо систему рівнянь,
які відповідають лініям
відповідає повне використання сировини
першого і другого видів, що означає, що
відповідні цим видам сировини нерівності
основної системи обмежень перетворились
на рівняння. Утворюємо систему рівнянь,
які відповідають лініям
![]() та
та
![]() :
:
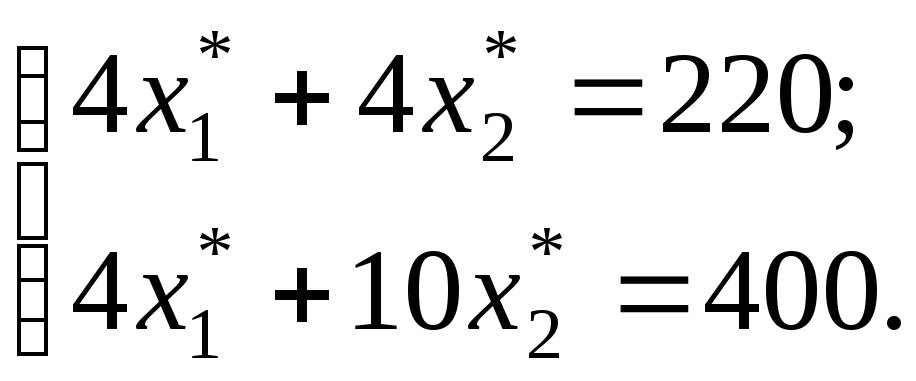
Розв’язком
цієї системи є оптимальний план
![]() .
.
4. За оптимальним планом задачі обчислюємо максимальне значення цільової функції:
![]() (ум.
од.).
(ум.
од.).
5. За оптимальним планом сировина 1-го та 2-го видів використана повністю. Визначимо надлишки інших видів сировини. Для цього підставимо значення оптимального плану до інших обмежень основної системи. Так, залишки сировини 3-го виду становлять
![]() ,
,
сировини 4-го виду
![]() .
.
Перетворимо
вихідну математичну модель задачі. Для
цього поряд з основними змінними, які
визначають кількість продукції кожного
типу, введемо додаткові
змінні.
Ці змінні визначають залишки сировини
кожного виду, вони вводяться у нерівності
основної системи обмежень з метою
перетворення їх на рівняння. Таким
чином, застосування додаткових змінних
дозволяє перейти від стандартної
форми
математичної моделі задачі лінійного
програмування до канонічної,
або основної.
Так, залишки сировини 1-го виду позначимо
![]() ,
2-го –
,
2-го –
![]() ,
3-го –
,
3-го –
![]() і 4-го –
і 4-го –
![]() .
Оскільки залишки сировини підприємство
не продає, то цільова функція, що визначає
прибуток підприємства, залишилась без
змін.
.
Оскільки залишки сировини підприємство
не продає, то цільова функція, що визначає
прибуток підприємства, залишилась без
змін.
Отже, математична модель задачі набуває вигляду:
![]() , (2.1ІІ)
, (2.1ІІ)
 (2.2ІІ)
(2.2ІІ)
![]() ,
,
![]() . (2.3ІІІ)
. (2.3ІІІ)
Знайдемо опорні розв’язки основної системи обмежень (2.2ІІ) за допомогою MS Excel (див. лабораторну роботу № 2 даного посібника). Для цього здійснимо перетворення розширеної матриці системи (2.2ІІ) за методом Жордана – Гаусса (рис. 2.2).
Зверніть
увагу, що додаткові змінні у системі
рівнянь (2.2ІІ)
утворюють одиничну матрицю
![]() ,
відповідно, її визначник не дорівнює
нулю. Отже, ранг матриці коефіцієнтів
системи дорівнює чотирьом, тоді кількість
базисних змінних теж дорівнює чотирьом,
а кількість вільних невідомих – двом.
Згідно з цим кількість загальних
розв’язків системи рівнянь визначається
як кількість сполучень з множини, що
містить шість елементів, по чотирьом.
Отже,
,
відповідно, її визначник не дорівнює
нулю. Отже, ранг матриці коефіцієнтів
системи дорівнює чотирьом, тоді кількість
базисних змінних теж дорівнює чотирьом,
а кількість вільних невідомих – двом.
Згідно з цим кількість загальних
розв’язків системи рівнянь визначається
як кількість сполучень з множини, що
містить шість елементів, по чотирьом.
Отже,
![]() .
.
Але не всі з цих рішень дають опорні плани задачі лінійного програмування.
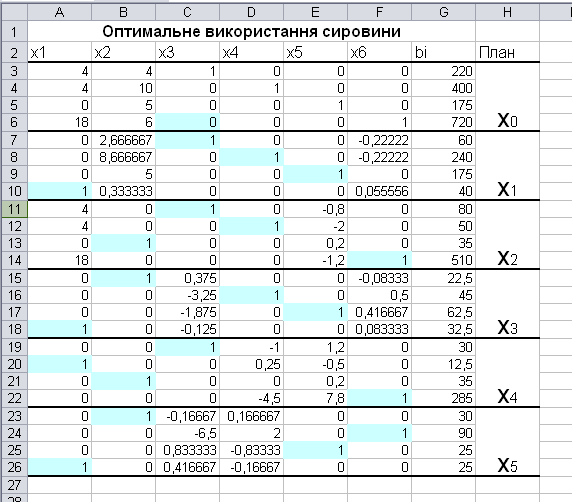
Рис. 2.2. Опорні плани задачі
Однак
многокутник планів має шість вершин,
звідси випливає, що система рівнянь
(2.2ІІ)
матиме лише шість опорних розв’язків.
Ці розв’язки є опорними планами задачі
про оптимальне використання сировини
і саме серед них треба шукати оптимальний
план. Так, вихідний план
![]() відповідає випадку, коли продукція не
виробляється, а вся кількість сировини
залишається не використаною. Йому
відповідає значення цільової функції
відповідає випадку, коли продукція не
виробляється, а вся кількість сировини
залишається не використаною. Йому
відповідає значення цільової функції
![]() .
План
.
План
![]() означає, що виробляється лише продукція
першого типу у кількості 40 одиниць, при
цьому сировина 4-го виду використана
повністю, залишки сировини 1-го виду
становлять 60 одиниць, 2-го – 240 одиниць,
3-го – 175 одиниць. За цим планом прибутки
підприємства при реалізації продукції
становитимуть
означає, що виробляється лише продукція
першого типу у кількості 40 одиниць, при
цьому сировина 4-го виду використана
повністю, залишки сировини 1-го виду
становлять 60 одиниць, 2-го – 240 одиниць,
3-го – 175 одиниць. За цим планом прибутки
підприємства при реалізації продукції
становитимуть
![]() (ум.
од.).
(ум.
од.).
Знайдемо прибуток підприємства за кожним з опорних планів. Так, обчислюємо значення цільової функції за кожним з опорних розв’язків:
![]() (ум.
од.);
(ум.
од.);
![]() (ум.
од.);
(ум.
од.);
![]() (ум.
од.);
(ум.
од.);
![]() (ум.
од.).
(ум.
од.).
До
речі, номер опорного плану відповідає
тому порядку, у якому лінія рівня цільової
функції перетинає вершини многокутника
планів, якщо її пересувати вздовж
градієнта цільової функції (див. рис.
2.1). Відповідно, із збільшенням номера
плану зростає і значення цільової
функції. Найбільше її значення відповідає
плану
![]() .
Цей план і є оптимальним планом виробництва
продукції:
.
Цей план і є оптимальним планом виробництва
продукції:
![]() .
.
Зверніть увагу, що при розв’язанні системи рівнянь (2.2ІІ) було отримано відомості не тільки про кількість продукції, яку підприємство виробляє за оптимальним планом, але і про залишки сировини кожного виду при виконанні цього плану.
Зрозуміло, що результати, які одержано при аналізі математичної моделі задачі, що надана у канонічній формі, співпадають з тими, які отримано раніше при аналізі математичної моделі задачі, що надана у стандартній формі.
