I. Кинематика материальной точки
Кинематика занимается описанием движения без выяснения его причин.
Материальной точкой называют физическую модель такого реального объекта, размерами которого можно пренебречь в конкретной задаче.
Прямая
задача кинематики - определить положение
тела в любой момент времени. Если речь
идёт о движении материальной точки, это
означает - определить зависимость
радиус-вектора точки от времени
по известному ускорению
.
Для этого необходимо знать начальные
условия - положение и скорость материальной
точки в начальный момент времени (t = 0).
Существуют три основных способа описания движения: векторный, координатный и естественный.
1. Векторный способ
В
этом способе положение материальной
точки задают радиус-вектором
,
проведенным из некоторой неподвижной
точки, называемой началом отсчета.
Рассмотрим алгоритм решения прямой задачи кинематики при векторном способе описания движения.
По известному ускорению материальной точки, находят скорость точки в произвольный момент времени
.
Постоянные интегрирования определяются, исходя из начальных условий (см. в примерах).
Определив
,
находят зависимость радиус-вектора от
времени
.
Если в задаче требуется определить модуль скорости тела, то он определяется как:
,
где
- проекции скорости на оси X,
Y,
Z
соответственно (их также можно называть
составляющими скорости по названным
осям).
Путь,
пройденный телом, определяется из
определения модуля скорости
как
.
Решение задач
1.1.
Положение материальной точки определяется
в момент времени t = 0
радиус-вектором
,
вектором скорости
и постоянным ускорением
,
направленным перпендикулярно скорости
.
Найти временную зависимость радиус-вектора
,
вектора скорости
и модуля скорости точки.
Решение. Скорость точки в произвольный момент времени равна
.
По
условию задачи
при
t = 0,
следовательно,
.
Поэтому
Зависимость радиус-вектора точки определяется выражением
Учитывая,
что по условию
при
t = 0
находим
.
Тогда
Так
как
(рис.1), зависимость от времени модуля
скорости тела определяется выражением
В
разобранной задаче была рассмотрена
прямая задача кинематики - по известному
ускорению и начальным условиям было
найдено местоположение материальной
точки в произвольный момент времени.
Однако, во многих случаях возникает и
обратная задача: по известному закону
определить
и
.
Если прямая задача выполнялась с помощью
математической операции интегрирования,
то обратная требует применения
дифференцирования.
1.2.
Радиус-вектор частицы меняется со
временем по закону
,
где
- постоянный вектор,
- положительная постоянная. Найти:
а)
скорость
и ускорение
частицы в зависимости от времени;
б) промежуток времени Δt, по истечении которого частица вернётся в исходную точку;
в) путь S, который она пройдёт при этом.
Решение. а) По определению скорость и ускорение в произвольный момент времени соответственно равны
,
.
б) По истечении времени Δt частица вернется в исходную точку, поэтому ее радиус-вектор равен нулю:
,
,
откуда
.
в) Путь, пройденный частицей, определяется соотношением
.
Модуль
скорости
- величина всегда положительная. Направим
ось X
вдоль вектора
,
тогда
,
при
и
,
при
и
.
На промежутке от 0 до t1:
.
На промежутке от t1 до Δt:
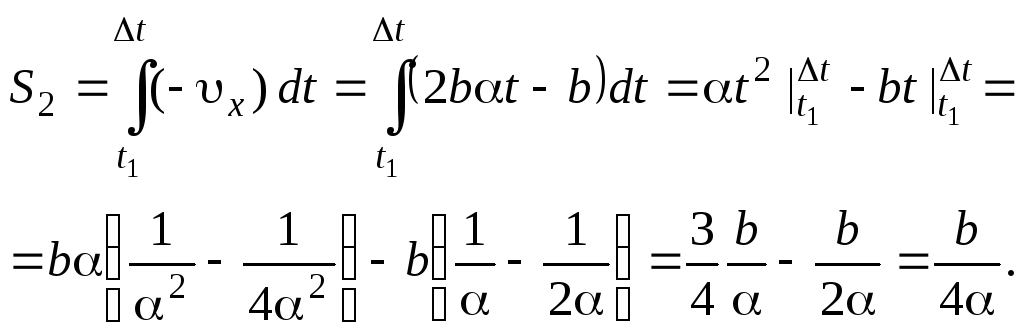
Путь, пройденный частицей
.
1.3*.
В момент t = 0
частица вышла из начала координат в
положительном направлении оси
.
Её скорость меняется со временем по
закону
,
где
- начальная скорость,
- некоторая положительная постоянная.
Найти:
а) ускорение и радиус-вектор;
б)
моменты времени, когда частица проходит
точку, удаленную на расстояние
от начала координат в случае, если
,
где
максимальное удаление точки от начала
отсчета оси
.
Решение.
а)
Продифференцировав
по времени, получим ускорение частицы
.
Представим радиус-вектор частицы как
.
По
условию
при
t = 0,
поэтому
и
.
б)
Поскольку частица движется вдоль оси
,
то ее положение определяется координатой
,
которая является проекцией вектора
и
равна:
.
Найдем
максимальную координату
,
приравняв производную
нулю:
,
и
по условию
.
Покажем,
что найденное значение
действительно является максимумом. Для
этого найдем вторую производную
и сравним ее с нулем
.
Из
полученного результата видно, что
,
следовательно,
действительно является максимальным
удалением точки от начала отсчета оси
.
Т
аким
образом, в момент времени
координата частицы равна
,
и частица меняет направление своего
движения на противоположное (рис.2). На
расстоянии
от начала координат частица будет
находиться в моменты времени, когда
,
то есть
,
.
Подставив
в это выражение
для определения t,
получим квадратные уравнения
,
или
.
Решая уравнения, получим искомые значения времени
,
.
Отметим,
что для существования первых двух корней
необходимо, чтобы
,
то есть
,
что соответствует условию задачи. Один
из полученных корней
является отрицательным и физического
смысла не имеет. Итак, частица проходит
точку, удаленную на расстояние
от начала координат, в момент времени
(до
поворота частицы)
и в моменты времени
(после
поворота частицы).
1.4.
Радиус-вектор меняется со временем по
закону
,
и
- положительные постоянные,
и
- орты осей
X
и Y.
Найти:
а) уравнение траектории точки y(x);
б)
зависимость от времени скорости
,
ускорения
и модулей этих величин;
в)
зависимость от времени угла
между скоростью и ускорением.
Решение.
а) Спроецируем
вектор
на оси X,
Y
и Z
и получим
зависимости координат от времени
,
,
.
Исключив
из полученной системы уравнений время
,
получим уравнение траектории 
.
Из которого видно, что траектория движения - парабола. График функции y(x) в плоскости XY схематично изображен на рис.3.
б) По определению
,
то есть
, 
.
,
поэтому
, 
.
Модули скорости и ускорения равны
,
.
в
)
Как видно из рис.3, угол
между скоростью и ускорением равен в
данной задаче углу между скоростью
и её составляющей по оси Y
,
Откуда
.
В
данной задаче угол
между векторами
,
ускорения
можно определить другим, более
универсальным способом, используя
свойство скалярного произведения двух
векторов:
.
Из которого следует, что
.
Откуда
.
Учитывая,
что согласно вспомогательному
тригонометрическому тождеству
,
приведем полученный результат к виду
,
что совпадает с результатом полученным ранее.
Однако, этот универсальный способ часто оказывается достаточно громоздким.