
- •1 Завдання, що вирішуються в курсовій роботі 5
- •2 Стадії виконання курсової роботи 5
- •3 Безпека мережі 5
- •1 Завдання, що вирішуються в курсовій роботі
- •2 Стадії виконання курсової роботи
- •3 Безпека мережі
- •Завдання №1. Шифр Цезаря.
- •Завдання №2. Алгоритм шифрування гост 28147-89.
- •Проста заміна
- •Завдання №3. Алгоритм шифрування rsa.
- •Криптографічна система rsa (Rivest-Shamir-Adleman)
- •Завдання №4. Функція хешування.
- •Завдання №5. Електронний цифровий підпис.
- •Завдання 6: розрахунок параметрів лінійного тракту волс
- •6.1. Розрахунок первинних параметрів оптичного волокна
- •6.2. Розрахунок вторинних параметрів оптичного волокна
- •6.3. Розрахунок швидкодії восп
- •6.4. Розрахунок порогу чутливості пром
- •6.5. Розрахунок загасання з'єднувачів ов
- •6.6. Розрахунок розподілу енергетичного потенціалу
- •6.7. Розрахунок довжини ділянок регенерації
- •Завдання №7. Сегментація мереж за допомогою масок
- •Список літератури
Завдання №3. Алгоритм шифрування rsa.
Алгоритм шифрування RSA відноситься до криптографічних систем з відкритим ключем. Криптосистеми з відкритим ключем (асиметричні криптосистеми) були розроблені в другій половині сімдесятих років ХХ сторіччя. У асиметричних криптосистемах процедури прямого і зворотного криптоперетворення виконуються на різних ключах і не мають між собою очевидних і таких зв'язків, що легко простежуються, що дозволяють по одному ключу визначити інший. У такій схемі знання тільки ключа шифрувания не дозволяє розшифрувати повідомлення, тому він не є секретним елементом шифру і зазвичай публікується учасником обміну для того, щоб будь-який охочий міг послати йому шифроване повідомлення.
Принцип функціонування асиметричної криптосистеми полягає в наступному:
-
користувач А генерує два ключі - відкритий (незасекречений) і секретний - і передає відкритий ключ по незахищеному каналу користувачеві Б;
-
користувач Б шифрує повідомлення, використовуючи відкритий ключ шифрування користувача А;
-
користувач Б посилає зашифроване повідомлення користувача А по незахищеному каналу;
-
користувач А отримує зашифроване повідомлення і дешифрує його, використовуючи свій секретний ключ.
Пари { відкритий ключ; секретний ключ} обчислюються за допомогою спеціальних алгоритмів, причому жоден ключ не може бути виведений з іншого.
Криптографічна система rsa (Rivest-Shamir-Adleman)
Авторами алгоритму RSA, запропонованого в 1977 р., є Р.Рівест (Rivest), А.Шамір (Shamir) і А.Адлеман (Adleman). Надійність алгоритму грунтується на трудності факторизації (розкладання на множники) великих чисел і труднощі обчислення дискретних алгоритмів (знаходження x при відомих а, b і n з рівняння ах = b (mod n) ).
Алгоритм RSA складається з трьох частин: генерації ключів, шифрування і дешифрування.
-
Генерація ключів.
Виберемо два великих різних простих числа p і q (Натуральне число називається простим, якщо воно ділиться тільки на себе і на 1.) і знайдемо їх добуток
n = pq .
Обчислимо функцію Ейлера (n) за формулою
(n) = (p-1)(q-1).
Закритий ключ d вибираємо з умов
d < (n) та
d взаємно просте з (n),
тобто d і (n) не мають загальних дільників.
Відкритий ключ e вибираємо з умов
e < (n) та
de = 1(mod (n)).
Остання умова означає, що різниця de - 1 винна ділитися на (n) без залишку. Для визначення числа e потрібно підібрати таке число, що
de - 1 = (n)*k .
У алгоритмі RSA
( e, n ) – відкритий ключ
( d, n ) – секретний ключ.
-
Шифрування.
Початкове повідомлення розбивається на блоки Mi однакової довжини. Кожен блок представляється у вигляді великого десяткового числа, меншого n, і шифрується окремо. Шифрування блоку M (M - десяткове число) здійснюється по наступній формулі
Me = C (mod n)
де C – шифроблок, відповідний блоку відкритого повідомлення M. Шифроблоки з'єднуються в шифрограму.
-
Дешифрування.
При дешифруванні шифрограма розбивається на блоки відомої довжини і кожен шифроблок розшифровується окремо по наступній формулі
Cd = M (mod n) .
Згенеруйте відкритий і закритий ключі в алгоритмі шифрування RSA, вибравши прості числа p і q з першої сотні. Зашифруйте повідомлення, що складається з ваших ініціалів: ПІБ.
I.Генерация ключів .
Виберемо двоє простих чисел р = 13 і q = 19 (див. Д5).
Тоді модуль
n = pq=13*19 = 247
і функція Ейлера
(n) = (p-1)(q-1) = 12*18 = 216.
Закритий ключ d вибираємо з умов d < (n) і d взаємно просто з (n), тобто d и (n) не мають загальних дільників.
Хай d = 25.
Відкритий ключ e вибираємо з умов e<(n) и de=1(mod (n)): e<216
25e=1(mod 216).
Остання умова означає, що число 25e-1 повинно ділитися на 216 без залишку.
Таким чином, для визначення e потрібно підібрати таке число, що
25e-1 = 216 k.
При k=14 отримуємо 25e=3024+1 або
e=121.
У нашому прикладі
(121, 247) – відкритий ключ,
( 25, 247) – секретний ключ.
II. Шифрування
Представимо шифроване повідомлення «КГЛ» як послідовність цілих чисел. Хай літера «К» відповідає числу 12, літера «Г» - числу 4 і літера «Л» - числу 13.
Зашифруємо повідомлення, використовуючи відкритий ключ (121, 247):
С1
= (![]() )
mod 247= 12
)
mod 247= 12
С2
= (
![]() )
mod 247=199
)
mod 247=199
С3
= (![]() )
mod 247= 91
)
mod 247= 91
Таким чином, початковому повідомленню (12, 4, 13) відповідає криптограма
(12, 199, 91).
III. Розшифрування
Розшифруємо повідомлення (12, 199, 91), користуючись секретним ключем (25,247):
М1
= (
![]() )
mod 247=12
)
mod 247=12
М2
= (![]() )
mod 247= 4
)
mod 247= 4
МЗ
= (
![]() )
mod 247=13
)
mod 247=13
В результаті розшифрування було отримано початкове повідомлення (12, 4, 13), тобто "КГЛ".
Зауваження.
-
Ч
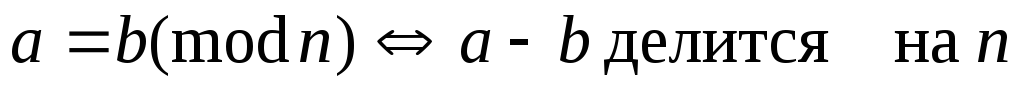
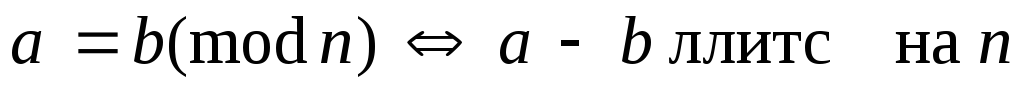 исла
а і
b
порівнянні
по mod
n, якщо
їх різниця ділиться на n:
исла
а і
b
порівнянні
по mod
n, якщо
їх різниця ділиться на n:
Наприклад,
![]() .
.
-
О
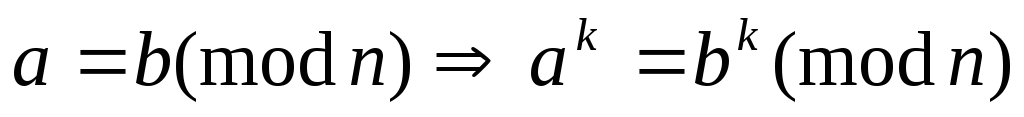
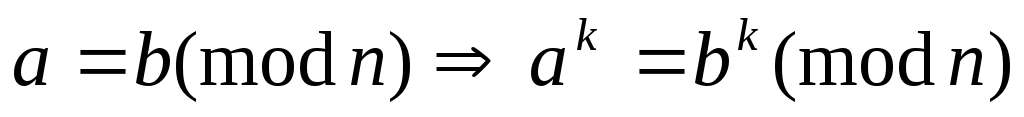 бчислення
можна проводити, використовуючи правила
модульної алгебри:
бчислення
можна проводити, використовуючи правила
модульної алгебри:
Для даного прикладу отримаємо
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() і
так далі.
і
так далі.
