
- •Русаков Алексей Михайлович
- •Лекции по дисциплине «Дискретная математика»
- •Введение.
- •Теория множеств.
- •Понятие множества. Операции над множествами.
- •Определение.
- •Определение.
- •Определение.
- •Пример.
- •Свойства операций сложения и пересечения множеств.
- •Определение.
- •Замечание.
- •Примеры.
- •Счётные множества. Теорема Кантора.
- •Определение.
- •Примеры счётных множеств.
- •Замечания.
- •Теорема.
- •Доказательство:
- •Задачи для самостоятельного решения.
- •Решите задачи № 1.30 1.39 с использованием диаграммы Эйлера-Венна.
- •Бинарные отношения в теории графов.
- •Например:
- •Матрицы смежности и инцидентности.
- •Пример.
- •Маршруты, цепи и простые цепи.
- •Определение
- •Расстояние и протяжённость в графе.
- •Деревья.
- •Примеры:
- •Например:
- •Помеченные графы. Перечисление помеченных деревьев.
- •Пример:
- •Теорема Келли.
- •Задача о кратчайшем соединении.
- •Задача о кратчайших путях.
- •Эйлеровы цепи, критерий Эйлеровости. Задача о Кёнигсбергских мостах.
- •Доказательство:
- •Достаточность.
- •Индуктивный переход.
- •Гамильтовы циклы.
- •Пример:
- •Примеры задач и упражнений.
- •Решение.
- •Задачи для самостоятельного решения.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение группы.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение и способы описания формальных грамматик.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Теория автоматов.
- •Основные понятия теории автоматов.
- •Определение.
- •Способы задания автоматов. Таблица переходов.
- •Определение.
- •Определение.
- •Способы задания автоматов. Граф автомата.
- •Определение.
- •Способы задания автоматов. Матрица переходов и выходов. Определение.
- •Машины Тьюринга и конечные автоматы. Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Машины Тьюринга с двумя выходами.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Автоматы с магазинной памятью и бесконтекстные языки.
- •Определение.
- •Определение.
- •Модель дискретного преобразователя Глушкова в. М. Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Понятие об абстрактном автомате и индуцируемом им отображении. Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Определение.
- •Автоматные отображения и события. Определение.
- •Определение.
- •Определение.
- •Определение.
- •Теорема.
- •Регулярные языки и конечные автоматы. Определение.
- •Определение.
- •Определение.
- •Определение.
- •Правила подчинения мест в регулярных выражениях.
- •Определение.
- •Определение.
- •Правила построения основного алгоритма синтеза конечных автоматов.
- •Пример.
- •Автомат Мили.
- •Определение.
- •Определение.
- •Автомат Мура.
- •Определение.
- •Определение.
- •Теория булевых функций.
- •Связь булевых функций и схем из функциональных элементов и контактных схем. Определение.
- •Замечания.
- •Теорема.
- •Доказательство:
- •Замечание.
- •Теорема. (Формулы разложения Клода Шеннона.)
- •Доказательство:
- •Замечания.
- •Основные свойства булевых функций. Замечание.
- •Определение.
- •Примеры задач и упражнений. Пример 1
- •Доказательство
- •Задачи для самостоятельного решения.
- •Элементы комбинаторики.
- •Основные понятия комбинаторики. Определение.
- •Определение.
- •Доказательство.
- •Теорема – правило включения-исключения.
- •Доказательство.
- •Доказательство.
- •8.2. Формулировка задания.
- •Определение.
- •Пример.
- •Переходы можно представить также с помощью таблицы и схематически:
- •Определение.
- •Последовательность выполнения.
- •Методический пример.
- •Контрольная распечатка.
- •Замечания.
- •Отчет по практической работе.
- •Контрольные вопросы
- •Варианты заданий.
- •Домашняя работа №1. По всей теории
- •Домашняя работа №2. Способы задания графов
- •8.03.2. Правила регулярного выражения.
- •Установка необходимого программного обеспечения.
- •Замечания.
- •Методический пример.
- •Контрольная распечатка.
- •Отчет по практической работе.
- •Контрольные вопросы.
- •Варианты заданий.
- •Дополнительные материалы.
- •Биография Георга Кантора (основатель теории множеств).
- •Город Калининград (Кёнигсберг).
- •Список литературы.
-
Бинарные отношения в теории графов.
Определение.
Бинарное отношение
![]() определяется как соотношение
определяется как соотношение
![]() ,
которое выполняется для некоторых пар
элементов заданного множества V.
,
которое выполняется для некоторых пар
элементов заданного множества V.
Между бинарными отношениями и графами с однократными рёбрами существует взаимно однозначное соответствие.
Так, например. Нуль — граф отвечает
нулевому отношению
![]() .
Полный граф
.
Полный граф
![]()
![]() отвечает универсальному отношению
отвечает универсальному отношению
![]() .
.
Каждое отношение
![]() имеет дополнительное отношение, или
отрицание
имеет дополнительное отношение, или
отрицание
![]()
![]() ,
такое что
,
такое что
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() не выполняется.
не выполняется.
Определение.
Граф
![]() является дополнением к Графу
является дополнением к Графу
![]() ,
то есть
,
то есть
![]() по отношению к полному графу
по отношению к полному графу
![]()
![]() ,
определённому на V.
,
определённому на V.
Определение.
Для любого отношения
![]() существует обратное отношение
существует обратное отношение
![]() ,
такое что
,
такое что
![]() тогда и только тогда, когда выполняется
тогда и только тогда, когда выполняется
![]() .
.
Определение.
Отношение
![]() называется частичным упорядочением,
если оно обладает следующими свойствами:
называется частичным упорядочением,
если оно обладает следующими свойствами:
-
Рефлексивность
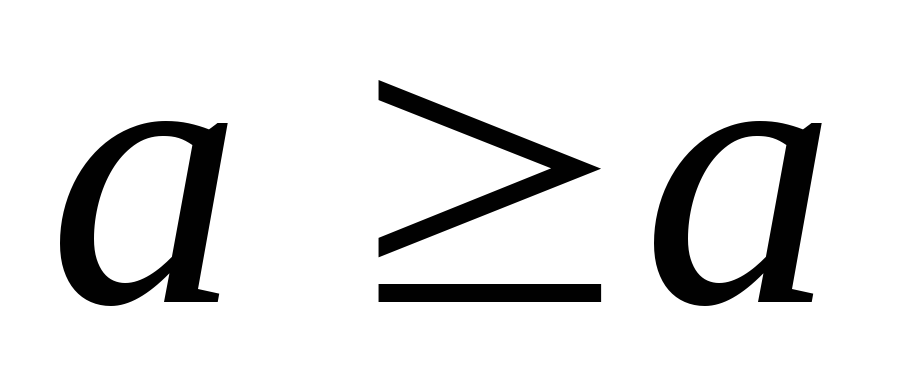 .
. -
Транзитивность. Из
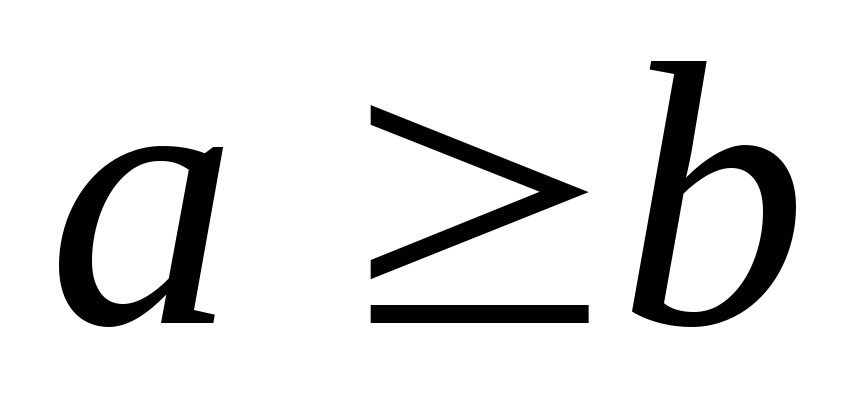 и
и
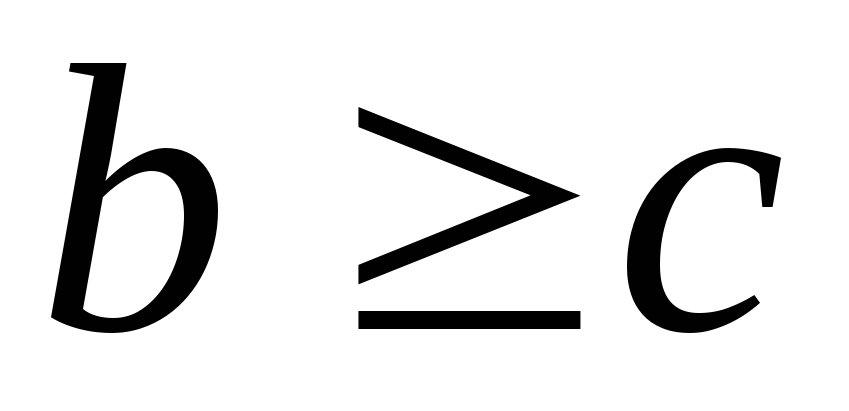 ,
следует
,
следует
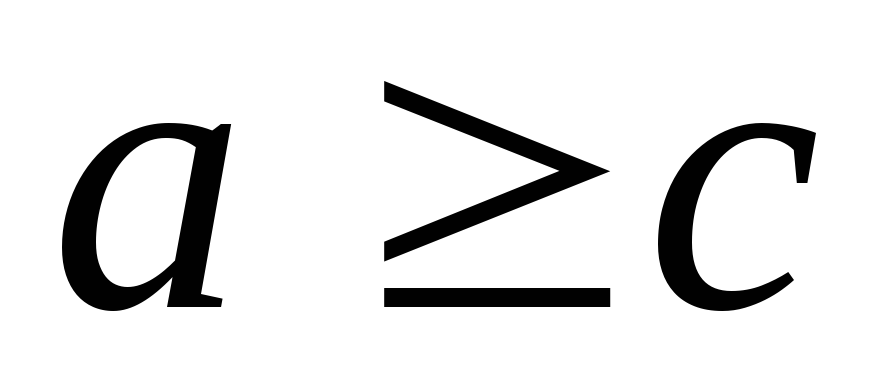 .
. -
Антисимметричность. Из
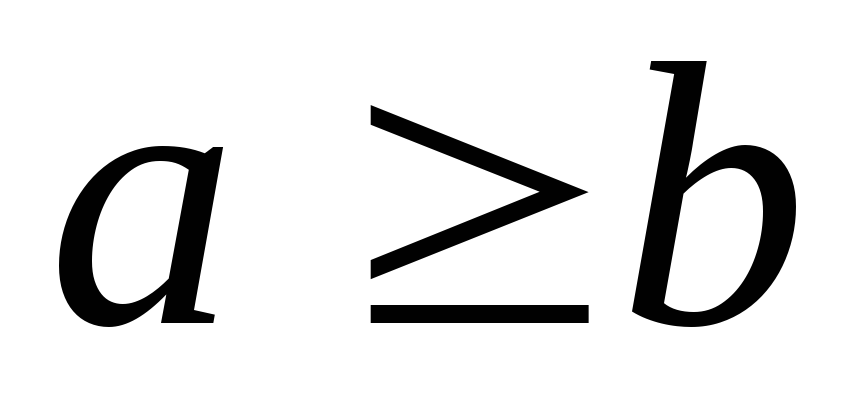 и
и
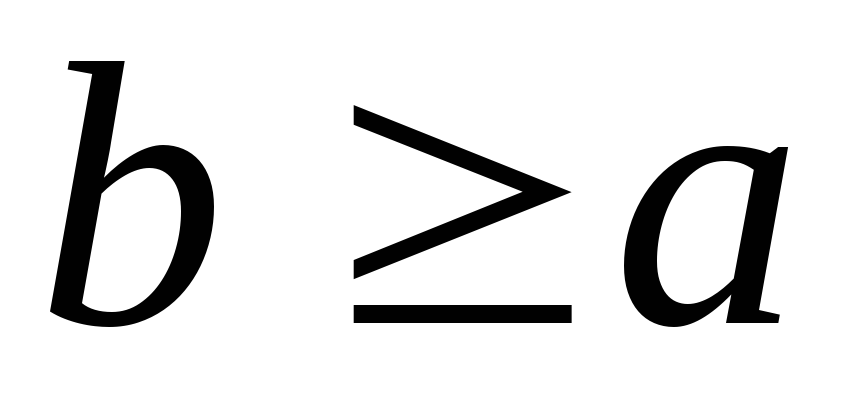 следует
следует
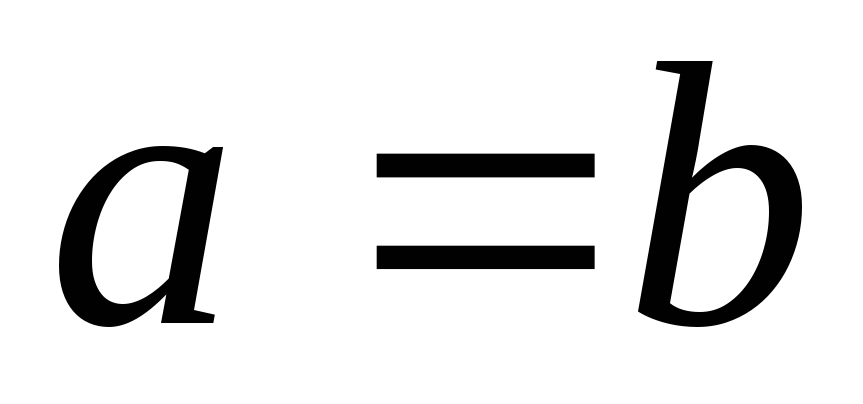 .
.
Соответствующий граф транзитивен, имеет петли, и любые две вершины в нём соединены не более чем одним ребром.
Например:
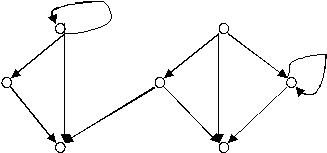
-
Матрицы смежности и инцидентности.
Во многих задачах теории графов (особенно решаемых на ЭВМ) графы удобно описывать матрицами.
Определение.
Пусть
![]() — помеченный конечный граф с
— помеченный конечный граф с
![]() вершинами и
вершинами и
![]() дугами (дуги тоже занумерованы).
дугами (дуги тоже занумерованы).
Матрицей смежности графа
![]() называется матрица
называется матрица
![]() размера
размера
![]() ,
определённая следующим образом:
,
определённая следующим образом:
![]()
Определение.
Матрицей инцидентности графа
называется матрица
![]() размера
размера
![]() ,
определённая следующим образом:
,
определённая следующим образом:

В случае неориентированного графа
матрица
![]() определяется следующим:
определяется следующим:

Пример.
Неориентированные и ориентированные
графы
![]() и
и
![]() можно представить в аналитической
форме, либо матрицей смежности
можно представить в аналитической
форме, либо матрицей смежности
![]() ,
либо матрицей инцидентности
,
либо матрицей инцидентности
![]() .
.
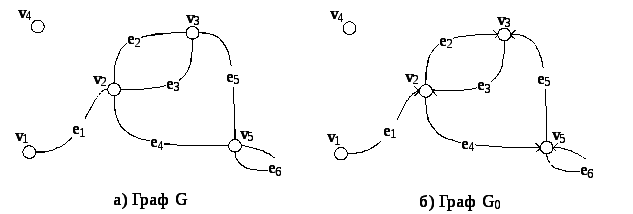
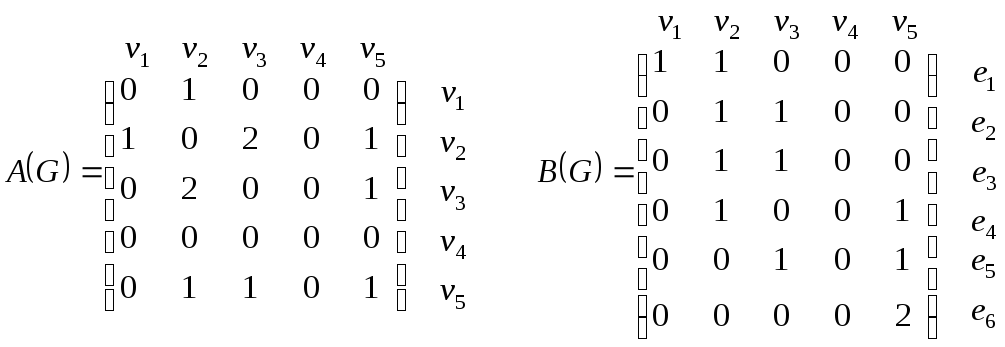
Матрица смежности (![]() )
для неориентированного графа (
)
для неориентированного графа (![]() )
всегда симметрична.
)
всегда симметрична.
Фигурирующая в ней двойка (2) или любое другое обозначение в некоторых случаях может быть заменена на единицу(1).
В матрице инцидентности сумма единиц
по столбцам указывает степень вершины
![]() .
.
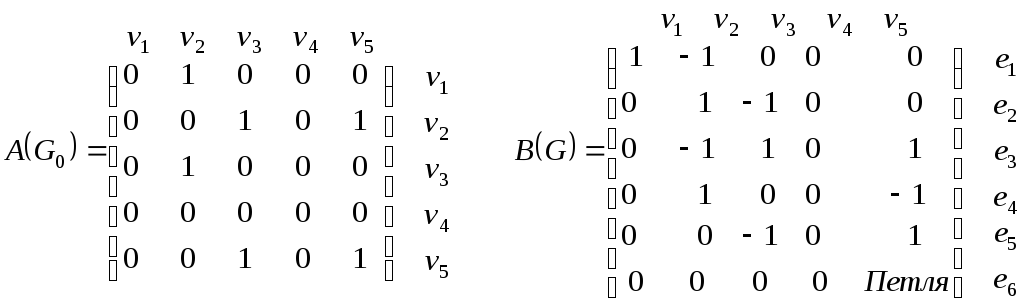
В общем случае матрица смежности для ориентированного графа уже не будет симметричной.
В матрице инцидентности ставится 1, если
дуга исходит из вершины и ![]() ,
если дуга заходит в неё.
,
если дуга заходит в неё.
Иногда, особенно графов с большим количеством вершин и дуг, вместо матриц смежности и инцидентности используются списковые структуры хранения элементов на их основе.
-
Маршруты, цепи и простые цепи.
Определение.
Маршрутом в графе
![]() называется такая конечная или бесконечная
последовательность рёбер
называется такая конечная или бесконечная
последовательность рёбер
![]() ,
что каждые два соседних ребра
,
что каждые два соседних ребра
![]() и
и
![]() имеют общую концевую точку. То есть
имеют общую концевую точку. То есть
![]() .
.
Замечания.
-
Одно и тоже ребро
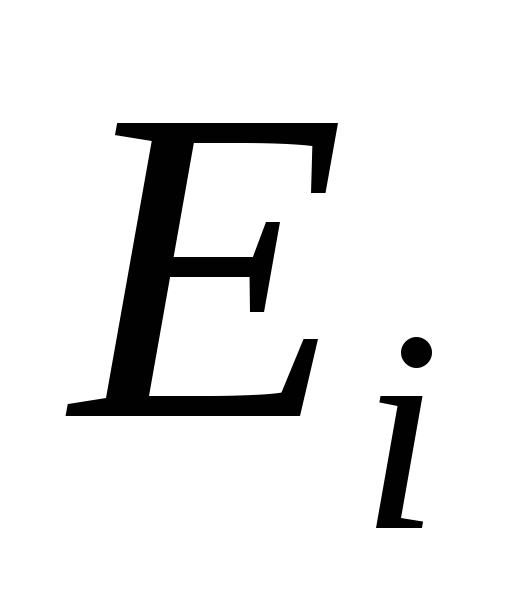 может встречаться в маршруте несколько
раз.
может встречаться в маршруте несколько
раз.
-
Если нет рёбер, предшествующих
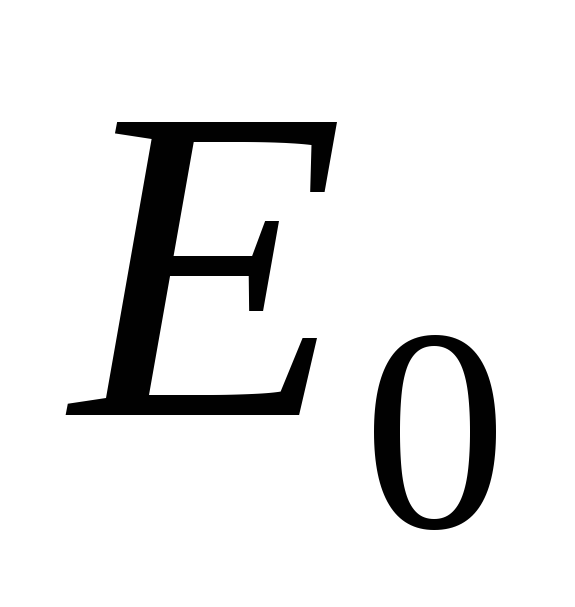 ,
то
,
то
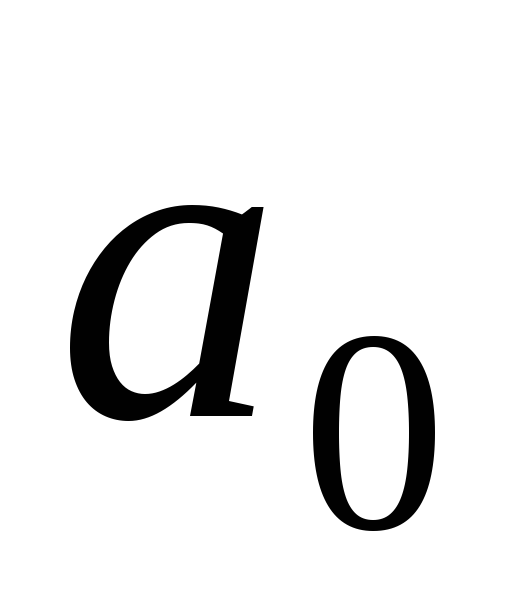 называется начальной вершиной
называется начальной вершиной
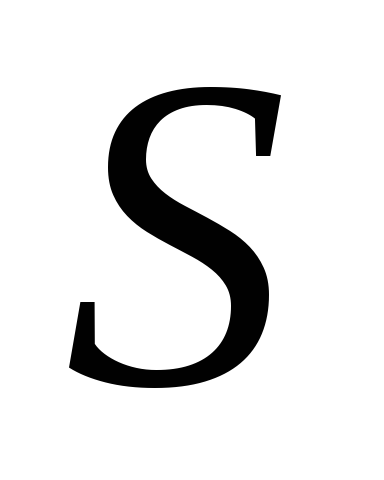 ,
а если нет рёбер, следующих за
,
а если нет рёбер, следующих за
 ,
то
,
то
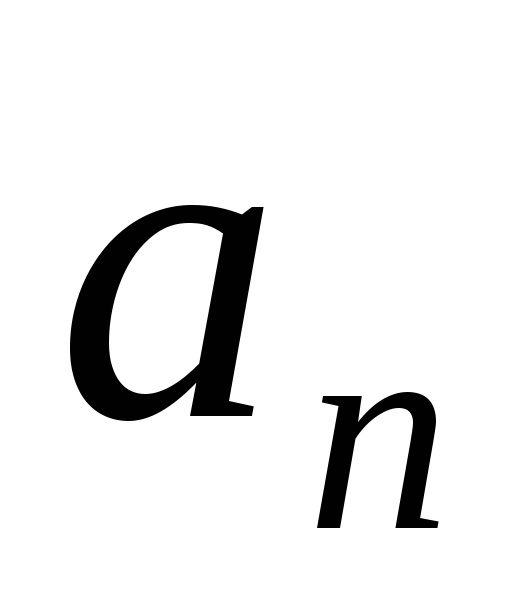 называется конечной вершиной
называется конечной вершиной
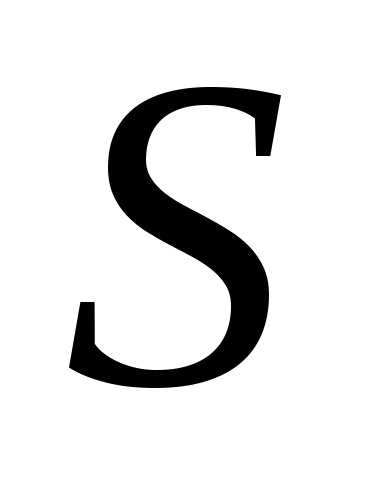 .
. -
Любая вершина
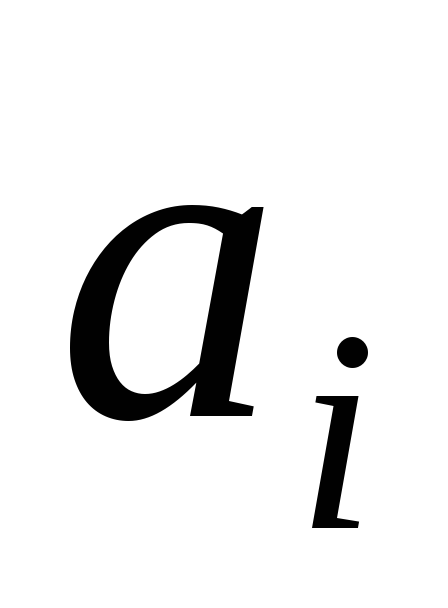 ,
принадлежащая двум соседним рёбрам
,
принадлежащая двум соседним рёбрам
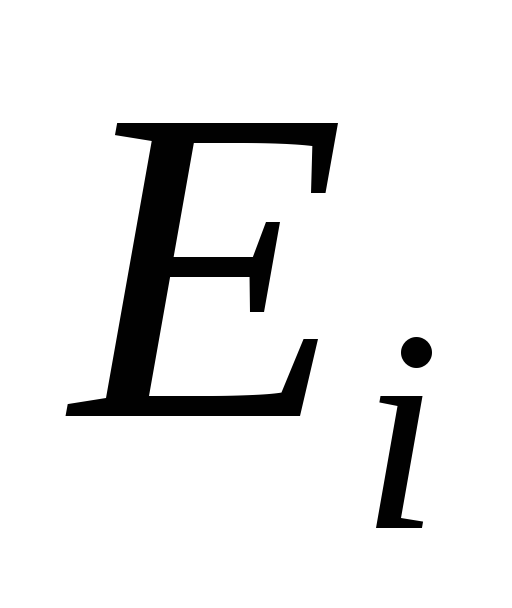 и
и
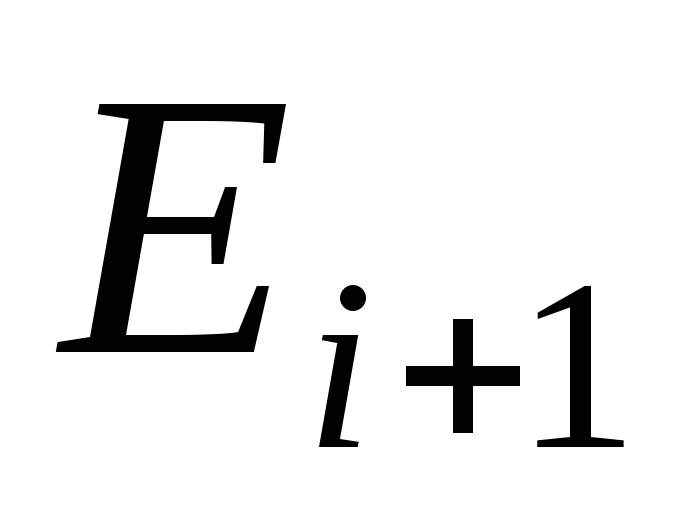 ,
называется внутренней или промежуточной
вершиной. Так как рёбра и вершины в
маршруте могут повторяться, внутренняя
вершина может также оказаться начальной
или конечной вершиной.
,
называется внутренней или промежуточной
вершиной. Так как рёбра и вершины в
маршруте могут повторяться, внутренняя
вершина может также оказаться начальной
или конечной вершиной.
Определение.
Если маршрут имеет начальную вершину, но не имеет конечной вершины или если он имеет конечную вершину, но не имеет начальной, то он называется односторонне бесконечным.
Определение.
Если маршрут не имеет ни начальной, ни конечной вершины, то он называется двусторонне-бесконечным.
Определение.
Маршрут называется цепью, а циклический маршрут — циклом, если каждое его ребро встречается в нём не более одного раза, а вершины в цепи могут повторяться и несколько раз.
Любой участок цепи есть цепь.
Определение.
Нециклическая цепь называется простой цепью, если в ней нет повторяющихся вершин.
Определение.
Цикл с концом
![]() называется простым циклом, если
называется простым циклом, если
![]() не является в нём промежуточной вершиной
и никакие другие вершины не повторяются.
не является в нём промежуточной вершиной
и никакие другие вершины не повторяются.
Участок простой цепи или простого цикла есть простая цепь.
-
Граф достижимости
Один из первых вопросов, возникающих при изучении графов, это вопрос о существовании путей между заданными или всеми парами вершин.
Определение
Отношение достижимости на
вершинах графа ![]() означает, что вершина w достижима из
вершины v, если v = w или вG есть путь
из v в w.
означает, что вершина w достижима из
вершины v, если v = w или вG есть путь
из v в w.
Иначе говоря, отношение достижимости является рефлексивным и транзитивным замыканием отношения E.
Для неориентированных графов это отношение также симметрично и, следовательно, является отношением эквивалентности на множестве вершин V.
Определение
В неориентированном графе классы эквивалентности по отношению достижимости называются связными компонентами.
Для ориентированных графов достижимость, вообще говоря, не должна быть симметричным отношением. Симметричной является взаимная достижимость.
Определение
Вершины v и w ориентированного графа G=(V,E) называются взаимно достижимыми, если в G есть путь из v в w и путь из w в v.
Ясно, что отношение взаимной достижимости является рефлексивным, симметричным и транзитивным и, следовательно, эквивалентностью на на множестве вершин графа.
Классы эквивалентности по отношению взаимной достижимости называются компонентами сильной связности или двусвязными компонентами графа.
Рассмотрим вначале вопрос о построении отношения достижимости. Определим для каждого графа его граф достижимости ( называемый иногда также графом транзитивного замыкания), ребра которого соответствуют путям исходного графа.
