7. Элементы комбинаторики.

   1. Основные понятия комбинаторики. Определение.

Комбинаторика — раздел математического анализа, посвященный способам под­счета числа элементов в конечных множествах.

Особенно полезными являются сами комбинаторные рассуждения. Они позволяют обойтись без излишнего формализма, и там, где эти прин­ципы срабатывают, получаются красивые и понятные результаты.

Ярким примером эффективности комбинаторного подхода является теория бинома Ньютона. Все красивые результаты — различные соотношения между биномиальными коэффициентами — имеют простое комбинаторное истолкование.

Определение.

Говорят, что отрезок натурального ряда нумерует множество , если существует биективное отображение .

Если задана нумерация множества , то применяют следующие обозначения:

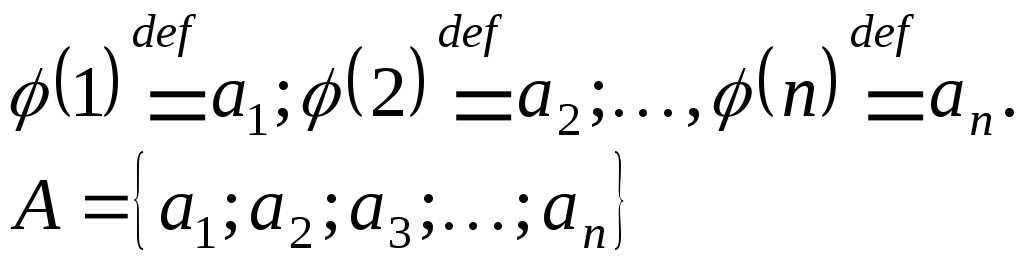
Теорема – правило суммы. Пусть и – конечные непересекающиеся множества, то есть , тогда

Доказательство.

Зафиксируем , нумерации и соответственно и рассмотрим отображение

,

заданное правилом:

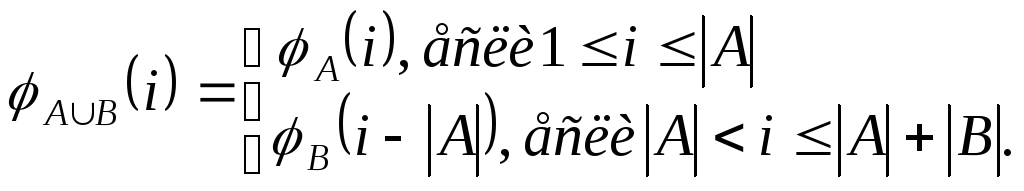
Очевидно, – биективное отображение, тогда на основании основного принципа комбинаторики получаем

.

Теорема (следствие из предыдущей). Пусть и – конечные множества, тогда .

Доказательство.

Очевидно, 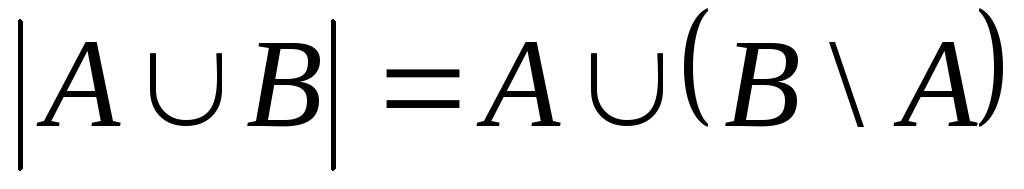и множества , не пересекаются тогда из равенства правила суммы получим

. (*)

Очевидно, 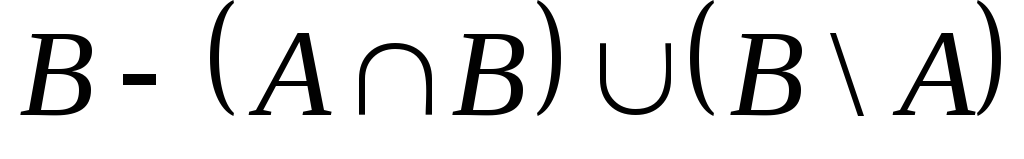и множества , тогда из равенства правила суммы получаем

. (**)

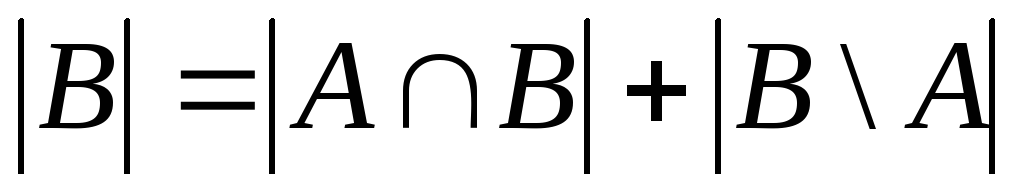Подставляя выражение для из (**) в (*), получаем

.

Теорема – правило включения-исключения.

Пусть – конечные множества, тогда

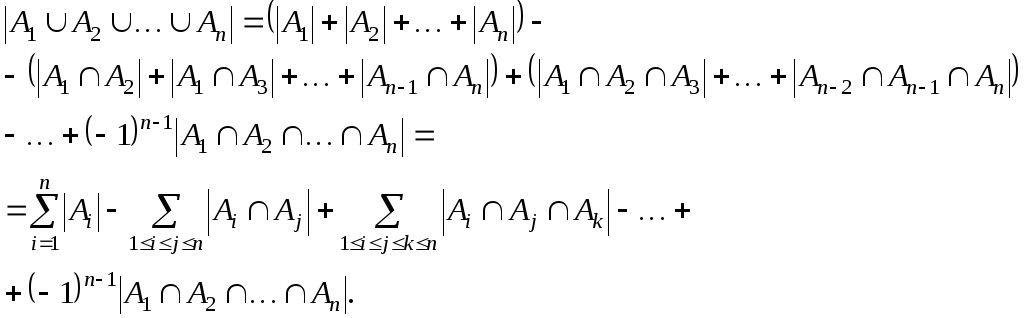
В правой части этой формулы, называемой формулой включения исключения, стоят с чередующимися знаками скобки, содержащие всевозможные попарные пересечения множеств , пересечения троек множеств и так далее.

Доказательство.

Докажем формулу включения-исключения по индукции.

Справедливость её для случая доказана в предыдущей теореме. Рассмотрим индуктивный переход, т.е. предположим, что формула верна для любых множества и покажем, что тогда она верна и для множеств.

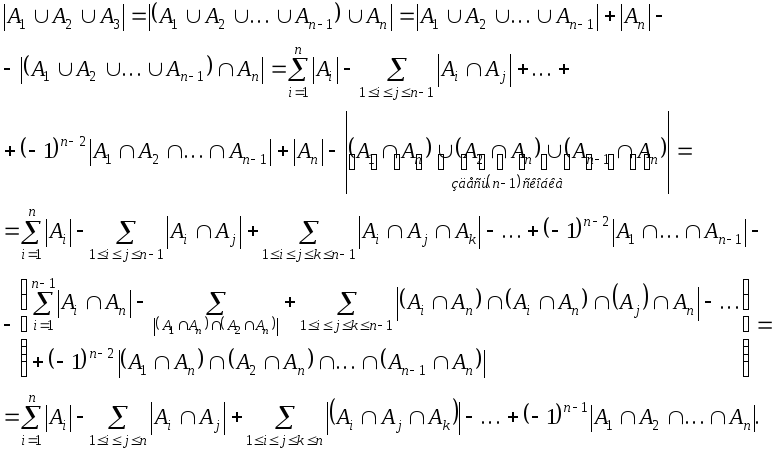
Здесь мы воспользовались равенствами

Теорема – правило суммы непересекающихся множеств.

Если – конечное попарно не пересекающиеся множества (т.е. ,), то

.

Ясно, что это тривиальное следствие из предыдущей теоремы.

2. Декартово произведение множеств.

Определение.

Декартовым произведением множества и называется множество, обозначенное , элементами которого являются упорядоченные пары , где , . Равенство упорядоченных пар понимается в следующем смысле:

пусть

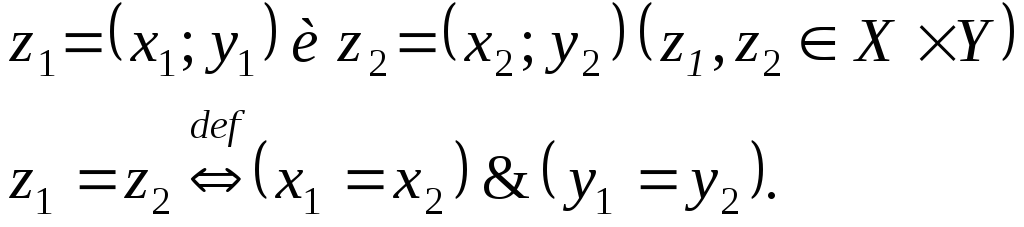
Теорема.

Если и – конечные множества, то – конечное множество и .

Доказательство.

Ясно, что в случае, когда одно из множеств , пусто, то и пусто и тривиально выполнено. Рассмотрим случай, когда и – непустые множества. Зафиксируем в нумерацию

.

Ясно, что и множества попарно не пересекаются, тогда по правилу суммы имеем:

(*).

Рассмотрим отображение , действующее по правилу

.

Ясно, что – биективное отображение, тогда по основному принципу комбинаторики получаем

(**).

Подставляя (**) в (*), получим:

.

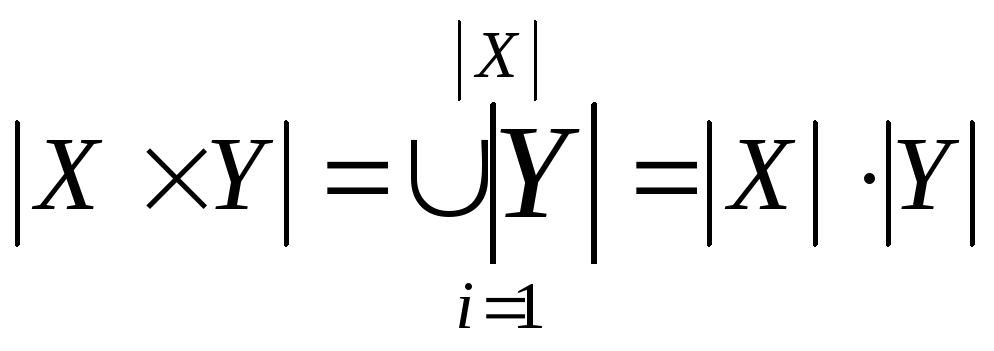3. Множество степень.

Определение.

Пусть – множество и . Определим декартовы степени множества следующими выражениями:

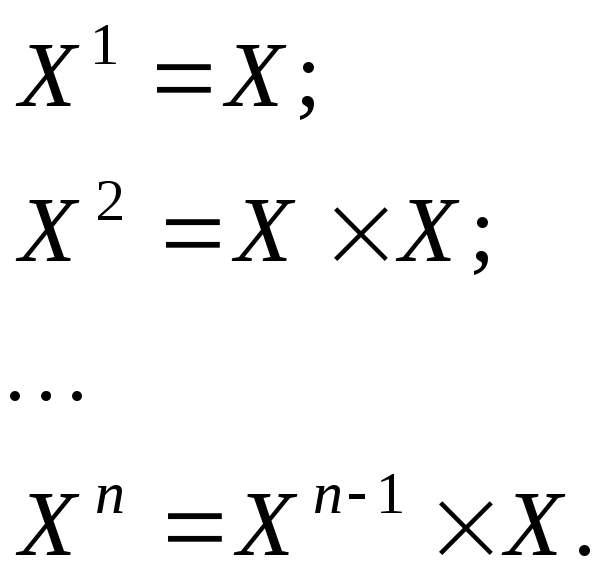
Теорема.

Если – конечное множество, то

.

Доказательство.

Ясно, что эта теорема является следствием из предыдущей теоремы.

Определение.

Пусть и – непустые множества. Обозначим через множество отображений, действующих из в , то есть

.

Множество называется множеством степень.

При доказательстве теоремы о числе элементов во множестве степень, когда и – конечные множества, необходимо доказать две леммы.

Лемма 1. Пустьи – конечные непустые множества и ,

тогда

.

Доказательство.

Зафиксируем в и нумерации – , .

Занумеруем элементы множества условием:

.

Ясно, что нумерующий отрезок – .

Лемма 2. Пустьи – конечные непустые множества и , , тогда

.

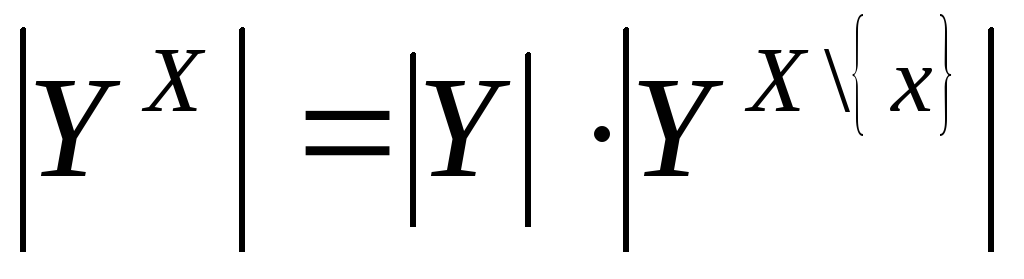Доказательство.

Зафиксируем в и нумерации, выбрав такую нумерацию множества , при которой .

Множество представим в виде объединения попарно непересекающихся множеств , отнеся ко множеству , если

.

По правилу суммы получаем:

. (*)

Рассмотрим одно из множеств . Каждое отображение однозначно определяется своим ограничением (сужением) на множество 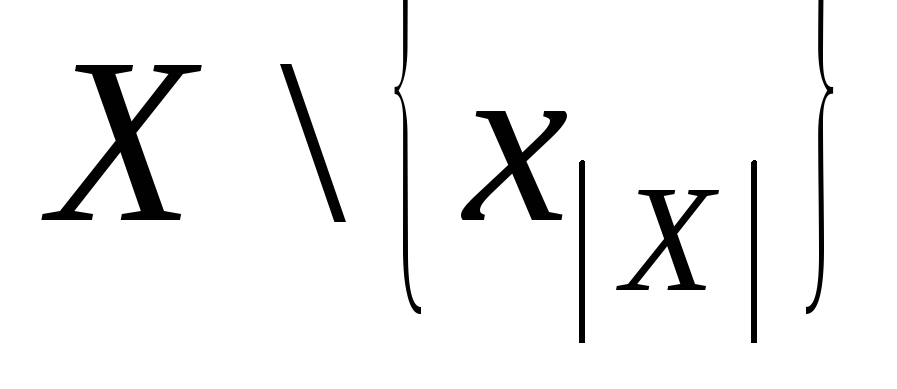. (Стрелочная диаграмма любого отображения , содержит стрелку, ведущую из в )

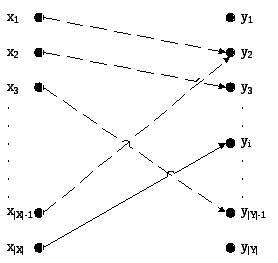
Стрелки указанные пунктиром – ограничение на .

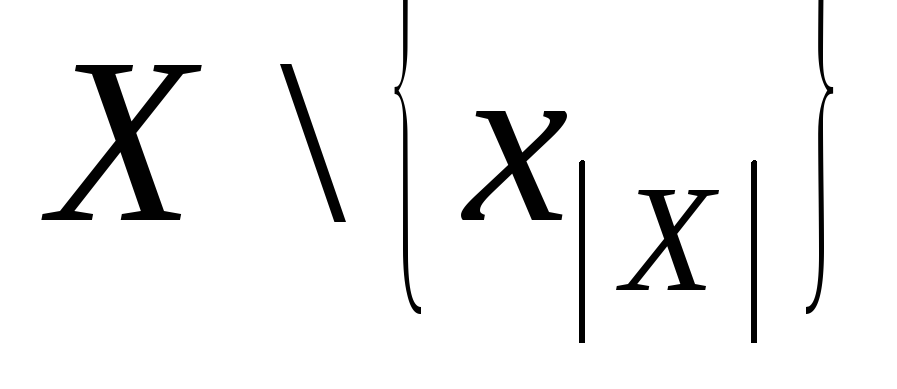Ясно, что . (**)

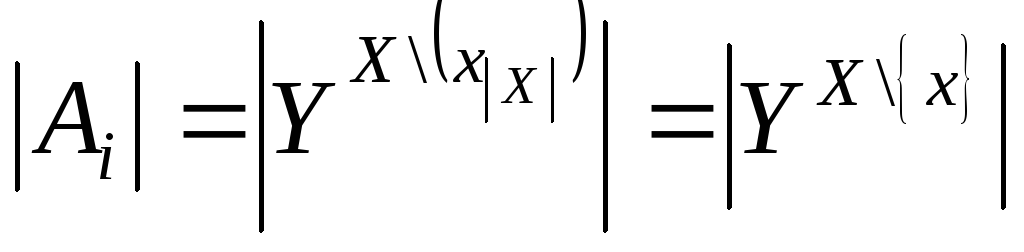Подставляя из (**) в (*), получаем

.

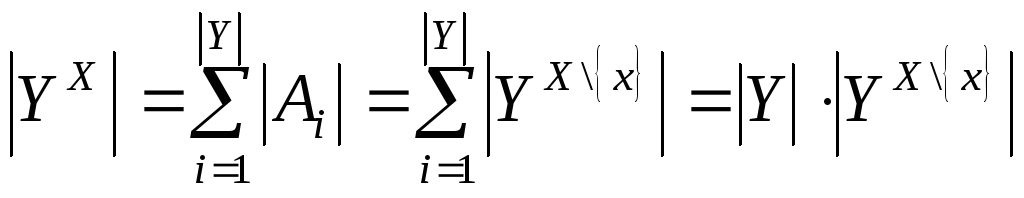Теорема. Пусть , – конечные непустые множества, тогда –конечное множество и

.