Замечания.

1. Учитывая, что существуют определённые аналитические преобразования одного логического базиса в другой, можно изображать схемы в любом логическом базисе и преобразовывать их в другие. Базис, состоящий из логических функций , ∧, ∨ называется нормальным; из логических функций ù, ∨ или ù, ∧ – неполным нормальным; из стрелки Пирса х ↓ у – базисом Вебба; из штриха Шеффера х ∣ у – базисом Шеффера.

Как известно, базис Вебба и базис Шеффера связаны с нормальным базисом следующими аналитическими соотношениями:

х ∣ у = ∨ ; и обратно, = х ∣ х; х ∨ у = (х ∣ х)∣(у ∣ у);

х ↓ у = ∧ ; и обратно, = х ↓ х; х ∧ у =(х ↓ х) ↓ (у ↓ у).

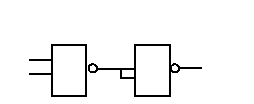
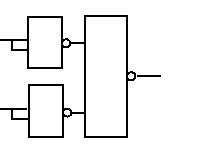
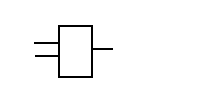
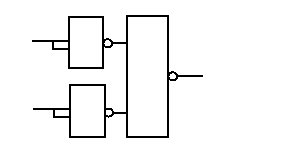
Переход от схемы в нормальном базисе к базисам Шеффера и Вебба и обратно, например, можно отобразить в следующей таблице (таблица 5.1).

Таблица 5.1.

Нормальный базис	Базис Шеффера	Базис Вебба
не
и
или

2. Логические функции, кроме их реализации функциональными схемами, реализуются также контактными, релейно-контактными и интегральными схемами.

3. Одна и та же схема (функциональная, контактная, релейно-контактная, интегральная) может быть реализована большим или меньшим числом функциональных базисных элементов (функций), для уменьшения которых, реализующих одну и ту же булеву функцию, разработана теория минимизации нормальных форм.

2. Основные понятия булевых функций.

Теорема.

Число всех различных булевых функций от n аргументов равно .

Доказательство:

Число различных наборов переменных x₁, x₂, … , x_n, где x_i {0,1} равно k=2ⁿ. Так как каждая булева функция принимает только 2 значения: 0 или 1, то число всех булевых функций от n переменных равно , что и требовалось доказать.

Определение.

Операцией сложения по модулю два, которая обозначается знаком , на множестве из двух элементов 0 и 1 называется операция со следующим законом композиции:

для a имеет место

a  a ≐ 0 ; a  0 0  a a .

Определение.

Элементарными булевыми функциями называются следующие функции:

e₁(x) 0 – нуль-функция;

e₂(x) 1 – единица-функция;

e₃(x) x – функция x;

e₄(x) = ù x – отрицание x;

e₅(x, y) ≐ – конъюнкция x и y;

e₆(x, y) ≐ – дизъюнкция x и y;

e₇(x, y) ≐ x  y – импликация x и y;

e₈(x, y) ≐ x  y – эквиваленция x и y;

e₉(x, y) x  y – сложение по модулю два x и y.

Замечания.

1. Таблица истинности для элементарных булевых функций имеет вид, представленный в табл. ниже.

Таблица

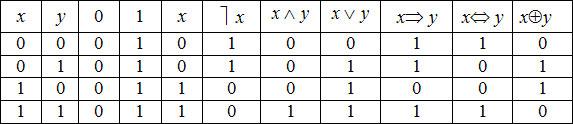
2. Заметим, что

1) x  y = ù ( x  y), то есть e₉(x, y) = e₄(e₈(x, y)), то есть функция xy является суперпозицией функций xy и ù x.

2) – суперпозиция функций и , каждая из которых от двух переменных.

3) 0 = ù (ù x); 1=ù x.

Приоритеты логических операций.

Операция ù имеет больший приоритет, чем ;

Операция имеет больший приоритет, чем ;

Операция  имеет больший приоритет, чем ;

Операция имеет больший приоритет, чем ;

Операция  имеет больший приоритет, чем .

Примеры функций, являющихся суперпозициями элементарных функций.

g₁(x₁, x₂, x₃, x₄) ≐  ù x₄

g₂(x₁, x₂, x₃) ≐ ù x₂)

g₃(x₁, x₂) ≐ ù

Определение.

Пусть

1) u – переменная, при этом пусть u⁰= ù u, а u¹=u;

2) a_i {0,1} , ;

3) u₁, u₂, … , u_n – переменные, причём не обязательно различные.

Тогда формула называется элементарной конъюнкцией, а – элементарной дизъюнкцией.

Примеры.

1. Элементарными конъюнкциями будут следующие формулы:

x, y, ù x, x  y, x₁  x_1, , , , .

2. Элементарными дизъюнкциями будут следующие формулы:

x,  y,  ù y,  x  y,  x  x  x, , ,  ,.

Ясно, что каждая элементарная конъюнкция и каждая элементарная дизъюнкция являются суперпозициями функций ù x, x  y и x  y.

Замечание.

Принимая для переменной u , что и , замечаем, что u^a = 1  u = a, a{0,1}.

В этом случае :

1) функция

K_n(x_1, x₂,…, x_n) = (1)

такая, что K_n(a_1, a₂,…, a_n) = 1 и K_n(b_1, b₂,…, b_n) = 0, если

(b_1, b₂,…, b_n)  (a_1, a₂,…, a_n);

2) функция

d_n(x_1, x₂,…, x_n)= (2)

такая, что d_n() = 0 и d_n(b_1, b₂,…, b_n) = 1, если

(b_1, b₂,…, b_n)  ().

При этом в формулах (1) и (2) все переменные попарно различны.