Определение.

Пересечением множеств и называется множество, состоящее из всех элементов, принадлежащих как , так и .

Пересечением любого (конечного или бесконечного) числа множеств называется совокупность элементов, принадлежащих каждому из множеств .

Рис. 1.2. .

Пример.

Пересечение множества всех четных чисел и множества чисел, делящихся на три, состоит из всех целых чисел, делящихся без остатка на шесть.

2. Свойства операций сложения и пересечения множеств.

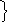. – коммутативность

.

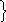. – ассоциативность

.

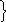. – взаимная

. дистрибутивность

Свойства 1. – 4. выполняются по определению.

Докажем свойство 5, то есть что .

Пусть х  . Это означает, что х  С и принадлежит по крайней мере одному из множеств А или В. Но тогда х   или , то есть х  множеству, записанному в правой части равенства 5.

Докажем обратное, то есть пусть х  . Тогда х   или х    х  С, а также х  А или х  В, то есть х    х  , то есть х  множеству, записанному в левой части равенства 5. Таким образом, равенство 5 доказано.

Определение.

Разность множеств А и В, обозначаемая как С = А \ В, – это совокупность тех элементов из А, которые не содержатся в В.

Рис. 1.3. С = А \ В.

Замечание.

1. При определении разности А \ В, вообще говоря, не предполагается, что А  В.

2. Иногда вместо А \ В пишут А – В.

Определение.

Симметрическая разность двух множеств А и В – это сумма разностей А \ В и В \ А, то есть

.

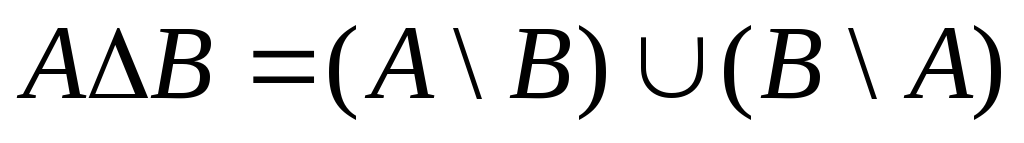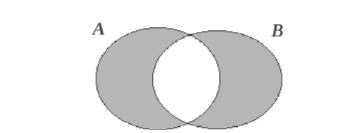
Рис. 1.4. С = А  В.

Замечание.

Название “симметрическая разность” для операции не совсем удачна. Операция во многом аналогична операции взятия суммы . Действительно, означает, что связываются неисключающим или два утверждения: “элемент  А” и “элемент  В”, а АВ означает, что эти же два утверждения связываются исключающим или, то есть х  АВ  х  либо только А, либо только В.

Множество АВ можно было бы назвать “суммой по модулю два” множеств А и В, то есть берётся объединение этих двух множеств, но элементы, которые при этом встречаются дважды, выбрасываются.

Определение.

Пусть S и А – множества, при этом A  S. Запас подмножеств S \ А называется дополнением множества А и обозначается СА или A  ( ).

1. Принцип двойственности в теории множеств.

1. Дополнение суммы равно пересечению дополнений:

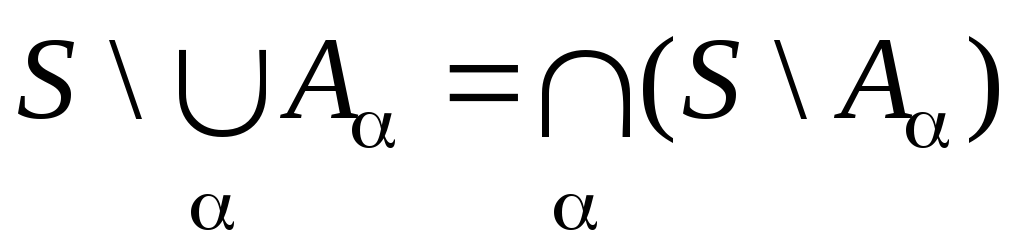. (1)

2. Дополнение пересечений равно сумме дополнений:

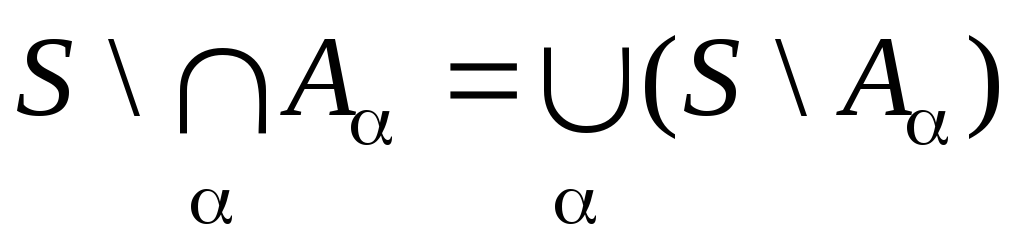. (2)

Докажем, например, соотношение 1.

Пусть . Это означает, что , то есть х  A_ для     х  S \ A_ для  .

Обратно, пусть х  , то есть х  S \ A_,   х  A_ для    .

Таким образом, равенство 1 доказано.

4. Отображения множеств.

Определение.

Пусть M и N – два произвольных множества. Если каждому элементу х  M поставлен в соответствие один и только один элемент y  N, то говорят, что на M определена функция ƒ, принимающая значения из N, то есть ƒ: M  N.

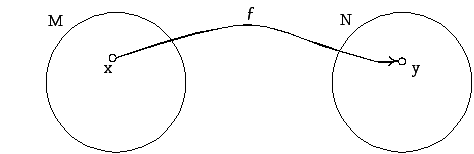
Рис. ƒ: M  N.

Замечания.

Для множеств произвольной природы часто вместо термина “функция” используется термин “отображение”.

При специализации природы множеств M и N возникают специальные типы функций, которые носят особые названия: “вектор-функция”, “мера”, “функционал”, “оператор” и т.д.

Определение.

Пусть а  M, ƒ: M  N. Тогда элемент b = ƒ(а)  N называется образом элемента а при отображении ƒ.

Определение.

Совокупность всех тех элементов а из M, образом которых при отображении ƒ является данный элемент b  N, называется прообразом (полным прообразом) элемента b и обозначается ƒ^–1(b).

Определение.

Пусть А, M, N – множества; ƒ: M  N; А  M. Тогда совокупность {ƒ(a) | a  A} всех элементов вида ƒ(а), где а  А, называется образом А и обозначается ƒ(А).

Определение.

Пусть

M, N, B – множества,

B  N,

ƒ: M  N.

Тогда совокупность {ƒ–1(b) | b  B} всех тех элементов из М, образы которых принадлежат В называется (полным) прообразом ƒ^–1(В) множества В при отображении ƒ.

Замечание.

Может оказаться, что ни один элемент b  B не имеет непустого прообраза, тогда и прообраз ƒ^–1(В) будет пустым множеством .

Определение.

Отображение ƒ: М  N есть отображение “на” множество N или сюръекция, если ƒ(М) = N.

Определение.

Отображение ƒ: М  N есть отображение множества М “в” множество N, если ƒ(М)  N.

Определение.

Пусть ƒ: М  N – отображение множества М “в” множество N, то есть ƒ(М)  N.

Если при х₁  х₂, где х₁  М, х₂  М, образы y₁ = ƒ(х₁) и y₂ = ƒ(х₂) различны, то есть y₁  y₂, то ƒ называется инъекцией.

Определение.

Отображение ƒ: М  N, которое одновременно является и сюръекцией и инъекцией, называется биекцией или взаимно однозначным соответствием между M и N.

Теорема.

Прообраз суммы двух множеств равен сумме их прообразов, то есть   ƒ^–1(А)ƒ^–1(В).

Доказательство:

Пусть х  ƒ^–1(). Это означает, что ƒ(х) , то есть ƒ(х)  А или ƒ(х)  В  х принадлежит по крайней мере одному из множеств ƒ^–1(А) или ƒ^–1(В), то есть х  ƒ^–1(А)ƒ^–1(В).

Обратно, пусть х  ƒ^–1(А)ƒ^–1(В), тогда х принадлежит по крайней мере одному из множеств ƒ^–1(А) или ƒ^–1(В), то есть ƒ(х) принадлежит хотя бы одному из множеств А или В  ƒ(х)   х  ƒ^–1(), что и требовалось доказать.

Теорема.

Прообраз пересечения двух множеств равен пересечению их прообразов, то есть ƒ^–1  ƒ^–1(А)ƒ^–1(В).

Доказательство:

Пусть х  ƒ^–1() ƒ(х)  АВ, то есть ƒ(х)  А  и  ƒ(х)  В. Следовательно, х  ƒ^–1(А) и х  ƒ^–1(В)  х  ƒ^–1(А)ƒ^–1(В). 

Обратно, пусть х  ƒ^–1(А)ƒ^–1(В), то есть х  ƒ^–1(А) и х  ƒ^–1(В)  ƒ(х)  А и ƒ(х)  В, то есть ƒ(х)  АВ  х  ƒ^–1(А В), что и требовалось доказать.

Теорема.

Образ суммы двух множеств равен сумме их образов, то есть ƒ  ƒ(А) ƒ(В).

Доказательство:

Пусть y  ƒ(АВ). Это означает, что y = ƒ(х), где х принадлежит по крайней мере одному из множеств А или В. Следовательно, y = ƒ(х)  ƒ(А)ƒ(В).

Обратно, пусть y  ƒ(А)ƒ(В)  y = ƒ(х), где х принадлежит по крайней мере одному из множеств А или В, то есть х  АВ  y = ƒ(х)  ƒ(АВ), что и требовалось доказать.

Замечания.

1. Последние три теоремы остаются в силе для сумм и пересечений любого (конечного или бесконечного) числа множеств.

2. Образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов.

Например, пусть задано отображение, проектирующее плоскость на ось х. Тогда отрезки

не пересекаются, а в то же время их образы  совпадают.

5. Разбиение на классы. Отношения эквивалентности.

На практике часто встречаются разбиения тех или иных множеств на попарно непересекающиеся подмножества.

Например,

1. плоскость, рассматриваемую как множество точек, можно разбить на прямые, параллельные оси х;

2. трехмерное пространство можно представить как объединение концентрических сфер различных радиусов, начиная с r = 0;

3. жителей данного города можно разбить на группы по их году рождения и т.п.