10. Помеченные графы. Перечисление помеченных деревьев.

Определение.

Граф с вершинами называется помеченным, если его множество вершин .

Определение.

Помеченные графы и с вершинами называются изоморфными, если существует биективное отображение такое, что (композиция) .

Замечание.

Это определение похоже на определение изоморфизмов теории графов, отличие состоит в том, что изоморфизм графов реализуется парой биективных отображений , , а — тождественное отображение.

Пример:

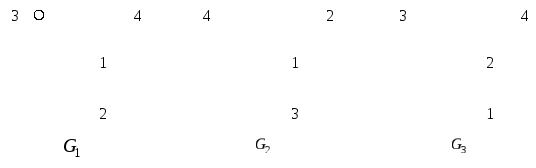
изоморфен как помеченный граф, графу и не изоморфен как помеченный графу .

Ясно, что в обычном смысле ,, изоморфны.

Задача.

Сколько существует не изоморфных между собой неориентированных помеченных деревьев с вершинами.

Обозначим число неизоморфных помеченных деревьев через . Ясно, что

Теорема Келли.

Свои результат по перечислению деревьев А. Келли успешно применил в жизни для определения количества химических изомеров углеродов C_nH_2n+2.

Структурные формулы таких молекул таких соединений (вершины — атомы, дуги — валентные связи) представляют собой деревья.

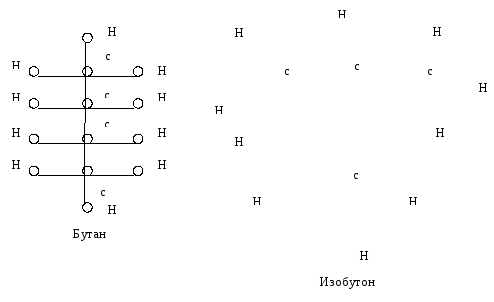
Важным для приложений классом ориентированных деревьев являются корневые, или растущие деревья, то есть такие, у которых существует вершина называемая корнем, из которой существуют простые пути во все остальные вершины (в силу общих свойств деревьев путь из корня в каждую вершину — единственный).

Вершины корневого дерева отличные от корня и висячих называют промежуточными. Такие структуры принято использовать для организации систем хранения информации, в частности, такими являются компьютерные файловые системы. Корневое дерево файловой системы обычно называют деревом директорий, в котором корень – корневая директория, промежуточные вершины – поддиректории, а висячие вершины – отдельные файлы или пустые поддиректории.

11. Задача о кратчайшем соединении.

Известны точки, в которых будут расположены населённые пункты (A,B,C,D,E) и известны трасы дорог (I,II,III,IV,V,VI,VII,VIII,IX,X), которые можно построить, а также стоимости из строительства (1,2,3,4,5,6).

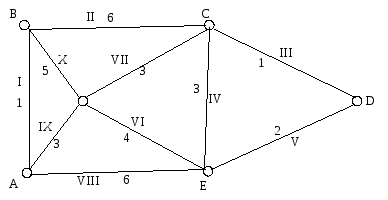
Ясно, что сформулированная задача может быть формализована с помощью теории графов.

Определение.

Взвешенным графом будем называть четверку , где — граф, .

Отображение называется весовым отображением.

Если , то называют весом дуги .

Если — путь или цепь на графе , то её весом называют величину: .

Весом графа называют величину .

Аналогично определяется вес подграфа и частичного графа.

Сформулируем задачу о соединении городов на языке теории графов: Дан конечный связный взвешенный граф . Требуется найти связный частичный граф минимального веса.

Определение.

Покрывающим деревом связного графа называется его частичный граф, который является деревом.

Если не является связным графом, то говорят о покрывающем лесе, то есть о деревьях, покрывающих его компоненты связности.

Теорема.

Решение задачи о соединении городов — покрывающее дерево.

Последовательность дуг покрывающего дерева минимального веса может быть найдена с помощью алгоритма Краскала. (В некоторых изданиях Крускала.)