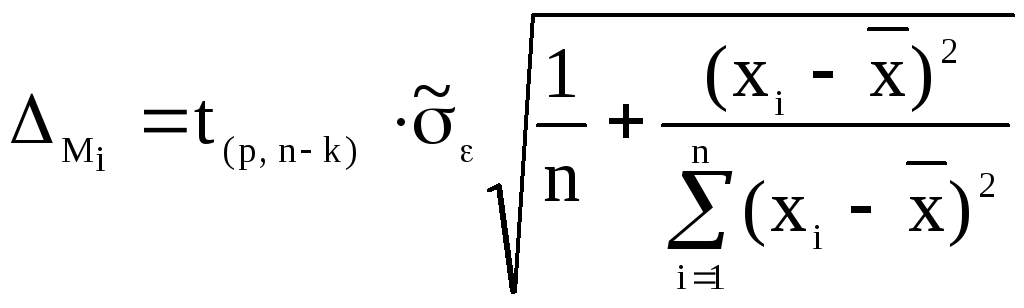Лабораторна робота №1 Парна лінійна регресія

Парна лінійна регресія.

ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.

Зв’язок між ознаками може бути функціональним (повним) і кореляційним (статистичним).

Функціональним називають такий зв’язок між ознаками, при якому кожному значенню однієї змінної (аргументу) відповідає тільки одне значення іншої змінної (функції). Такі зв’язки зустрічаються в математиці, фізиці, хімії і в інших науках.

Наприклад, площина кола (S=R²) і довжина окружності (C=2R) повністю визначаються радіусом R, площина трикутника – його сторонами.

В соціально – економічних явищах функціональні зв’язки між ознаками зустрічаються рідко. Тут найчастіше зустрічаються такі зв’язки між змінними величинами, при яких числовому значенню однієї з них відповідає декілька значень інших. Такий зв’язок між ознаками називається кореляційним (статистичним). Наприклад, відомо, що врожайність залежить від кількості внесених добрив, але на неї впливають і інші фактори (якість ґрунту, опади та інші). Крім того, однакова доза добрив при однакових умовах, часто по різному впливає на врожайність.

Кореляційний зв’язок є неповним, оскільки він виявляється при великій кількості спостережень та при порівнянні середніх значень результативної і факторної ознак. Він виражається відповідними математичними рівняннями.

В економічних дослідженнях часто розглядається лінійна форма зв’язку. Наприклад, зв’язок між витратами на відпустку та складом родини; витратами на рекламу та обсягом продукції, що випускається; витратами на споживання та валовим національним продуктом (ВНП); зміною ВНП від часу і т. ін.

Ця форма зв’язку виражається рівнянням прямої лінії

=b₀+b₁x,

де – вектор розрахункових значень результативної ознаки (залежна змінна) ;

х – вектор спостережень за незалежною змінною (значення факторної ознаки) х=x₁, x₂, … x_n;

b₀, b₁ – розрахункові параметри регресійної моделі.

Моделі, які встановлюють лінійну залежність між двома змінними і лінійні за своїми параметрами називаються простими лінійними регресійними моделями або лінійними моделями.

Рівняння типу =b₀+b₁x, називається рівнянням регресії або кореляційним рівнянням. Головною його метою є встановлення кількісного взаємозв’язку між ознаками.

Формально параметр b₀ – початок відліку або значення при х=0 ( тобто точка перетину з віссю ординат). Цей параметр може не мати економічного зміста. Спроби економічно інтерпретувати параметр b₀ можуть привести до абсурду, особливо, якщо b₀<0.

Інтерпретувати можливо лише знак при параметрі b₀. Якщо b₀>0, то відносне змінення результату відбувається повільніше, ніж зміна фактору. Іншими словами, варіація результату менше варіації фактору – коефіцієнт варіації по фактору x вищий за коефіцієнт варіації для результату y: V_x>V_y.

Параметр b₁ – нахил або коефіцієнт регресії, який показує середнє змінення залежної змінної при зміненні незалежної змінної на одиницю. Коефіцієнт регресії завжди має найменування. Якщо b₁>0, то зв’язок між ознаками прямий, якщо b₁<0, то зв’язок зворотній, якщо b₁=0, лінійний зв’язок відсутній.

Параметри рівняння b₀ і b₁ визначаються способом найменших квадратів, який дає можливість знайти таку теоретичну лінію регресії, яка у порівнянні з іншими проходить найбільш близько до всіх точок кореляційного поля, яке зображує фактичні дані, тобто дає найменшу суму квадратів відхилень фактичних значень результативної ознаки від вирівняних (теоретичних, розрахункових) значень:

Точкові оцінки параметрів, обчислених за методом найменших квадратів:

b₁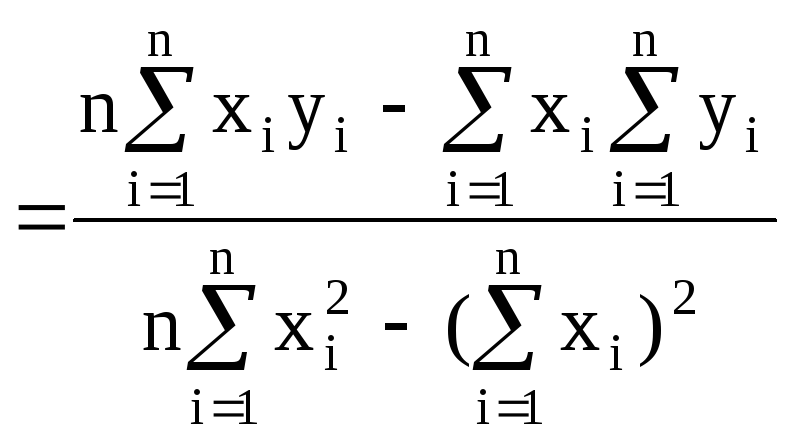 або b₁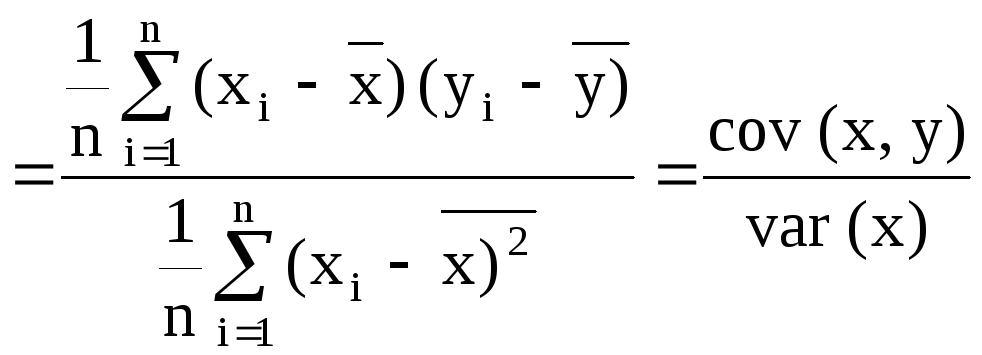

b₀=–b₁

Узагальненою регресійною моделлю є y=β₀+β₁x+ε, де β₀, β₁ – правильні параметри всієї генеральної сукупності, ε – неспостережувана випадкова величина. Коли параметри вибіркової лінійної моделі розраховані за методом найменших квадратів, то при певних класичних припущеннях математичне сподівання параметрів b₀ та b₁ дорівнює значенням параметрів узагальненої моделі β₀ і β₁.

При вивченні кореляційного зв’язку виникає необхідність разом з рішенням рівняння регресії знайти показник, який би характеризував ступінь щільності зв’язку між ознаками. При використанні лінійної регресії в якості такого показника виступає лінійний коефіцієнтом кореляції r_xy.

Існують різні модифікації формули лінійного коефіцієнту кореляції. Деякі з них наведені нижче:

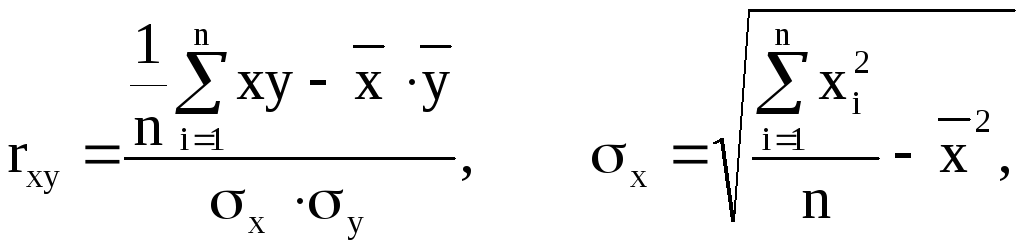
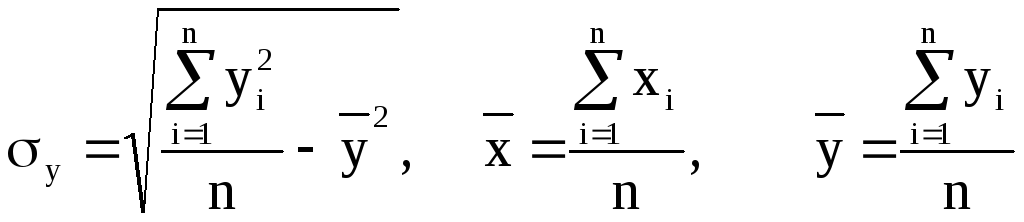
Або r_xy=b₁, чи .

Значення коефіцієнту кореляції знаходиться в межах від 0 до + 1. Якщо коефіцієнт кореляції дорівнює 0, то лінійний зв’язок відсутній, а якщо 1, то зв’язок функціональний. Знак + біля значення коефіцієнта кореляції, вказує на напрямок зв’язку (“+” – прямий, “–“ – зворотній). Чим ближче коефіцієнт кореляції до одиниці, тим зв’язок між ознаками щільніший:

r_xy<0,1 – зв’язку немає;

0,10,3 – зв’язок слабкий;

0,30,5 – зв’язок помірний;

0,50,7 – зв’язок помітний;

0,70,9 – зв’язок сильний;

0,90,99 – зв’язок дуже сильний;

0,991 – зв’язок повний.

Для оцінки якості підбору лінійної функції розраховується квадрат коефіцієнту кореляції , який називається коефіцієнтом детермінації. Він показує, яка доля загальної варіації ознаки визначається фактором, що вивчається, тобто характеризує долю дисперсії результативної ознаки y, що пояснюється регресією, в загальній дисперсії результативної ознаки:

.

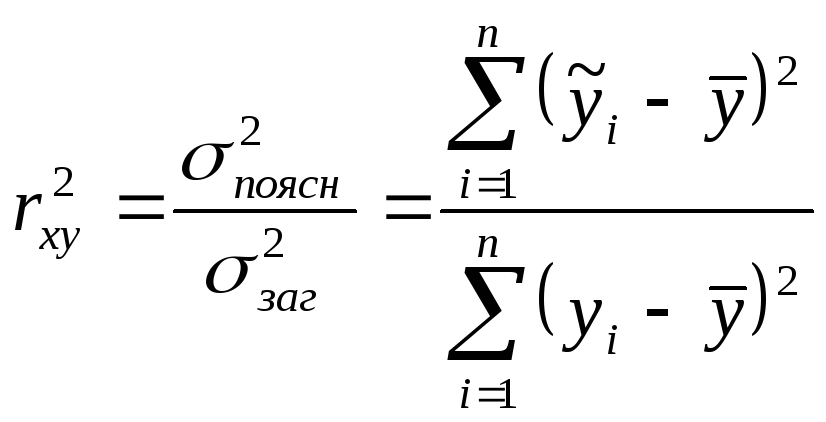n – об’єм вибірки;

– розрахункові значення, які отримані за формулою ;

y_i – статистичні значення, тобто початкові значення, на базі яких проводились розрахунки параметрів моделі;

– середнє значення залежного фактору .

Якщо коефіцієнт детермінації визначається у відсотках, то його слід читати наступним чином: варіація залежної змінної на стільки-то відсотків обумовлена варіацією фактора.

Адекватність простої лінійної регресійної моделі можна перевірити за допомогою коефіцієнта детермінації. Якщо його значення близьке до одиниці, то можна вважати, що модель адекватна. Якщо його значення близьке до 0, то модель неадекватна, тобто немає лінійного зв’язку між залежною та незалежною змінними.

Найпоширенішим критерієм, який надає можливість зробити висновок про адекватність моделі є критерій Фішера. Нагадаємо, що формулюється нуль – гіпотеза рівності нулеві значення коефіцієнта b₁ на противагу альтернативній гіпотезі, що цей параметр не дорівнює нулю, тобто має місце регресійний зв’язок і модель адекватна. При цьому нуль – гіпотеза має вигляд : H₀ : β₁=0, альтернативна H₁ : β₁≠0

Перевірка моделі на адекватність за F – критерієм Фішера передбачає здійснення певних етапів:

1. На першому етапі розрахуємо величину так званого F-відношення:

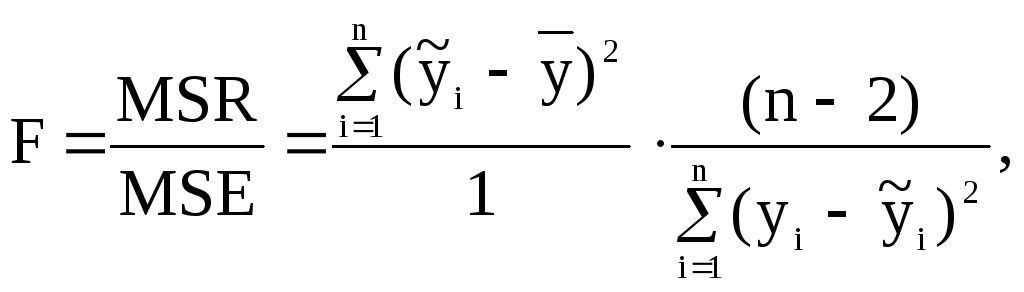
де MSR – середній квадрат, який можна пояснити з регресійної моделі;

MSE – середній квадрат помилок;

n – об’єм вибірки;

– розрахункові значення, які отримані за формулою ;

y_i – статистичні значення;

– середнє значення залежного фактору .

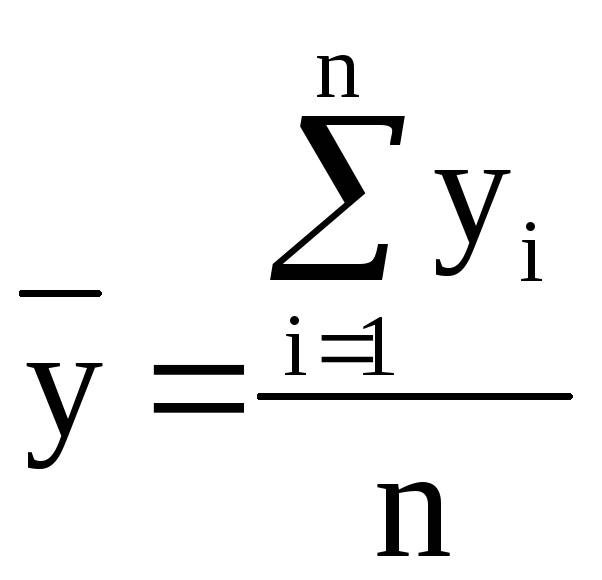2. На другому етапі задаємо рівень значимості α або α∙100%. Наприклад, якщо ми вважаємо, що можлива помилка α для нас становить 0,05 (або 5%), це означає, що ми можемо помилитися не більш ніж у 5% випадках, а в 95% випадків наші висновки будуть правильними.

3. На третьому етапі за статистичними таблицями F- розподілу Фішера або використовуючи спеціальні статистичні пакети або функції для лінійної моделі з (1, n–2) ступенями вільності і з надійністю р=100∙(1– α) % обчислимо критичне значення (F_кр або F_{(p,1, n-2)}).

4. Якщо розраховане нами значення F > F_{(p, 1, n-2)}, то ми відкидаємо гіпотезу Н₀, що =0 (або що (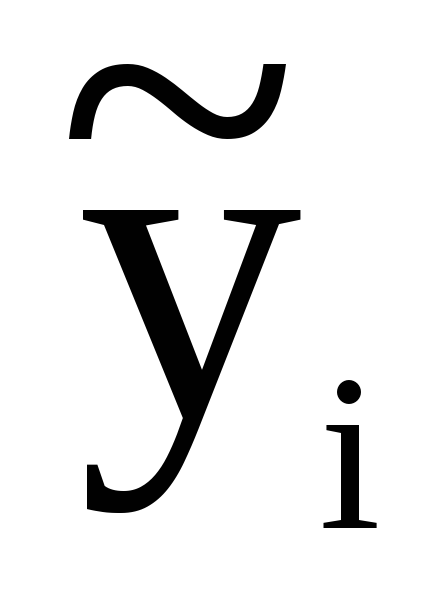=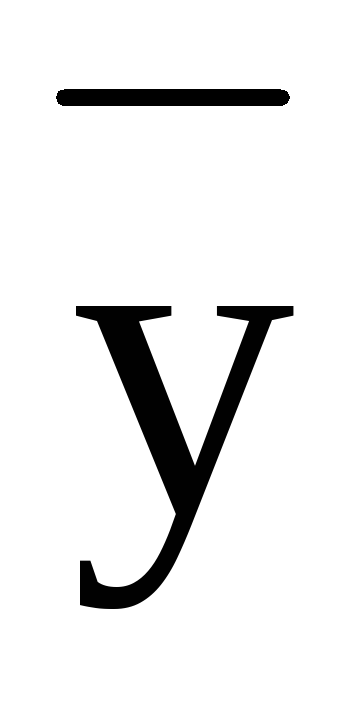) з ризиком помилитися не більш ніж у α∙100% випадках.

Отже, якщо F>F_{(p, 1, n-2).}, то побудована нами модель адекватна реальній дійсності.

Величина F – критерію пов’язана з коефіцієнтом детермінації:

.

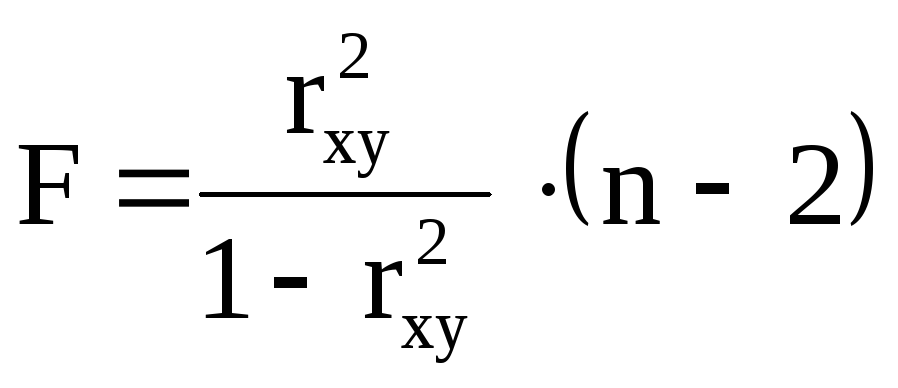Оцінка значимості рівняння регресії робиться у вигляді таблиці дисперсійного аналізу. Наведемо її приклад для лінійної моделі:

Джерело варіації	Число ступенів свободи	Сума квадратів відхилень	Дисперсія на одну ступінь свободи
Загальне	n-1
Зумовлене регресією (пояснене)	1
Не пояснюване за допомогою регресії (помилка, залишкове)	n-2

Величину стандартної помилки сумісно з t – розподілом Ст'юдента при n-2 ступенях свободи використовується для перевірки суттєвості параметрів моделі кореляції і для розрахунку їх довірчих інтервалів.

Для перевірки параметрів b₀ і b₁ на значимість використаємо t- тест Ст’юдента. Формулюємо нуль – гіпотезу H₀ : β_i=0 проти альтернативної H₀ : β_i≠0, i=.

Знайдемо спочатку оцінку дисперсії кожного параметра

,

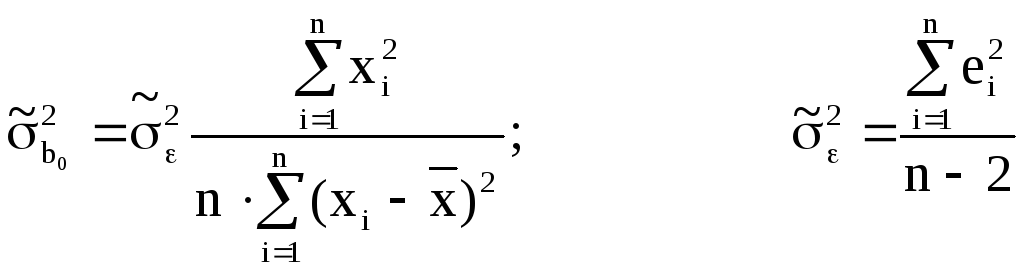
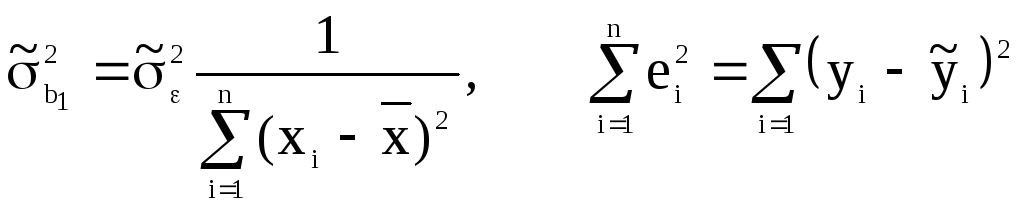п – об’єм вибірки

Розрахуємо значення t- статистики для обох параметрів:

, i=.

За статистичними таблицями критичних точок розподілу Ст’юдента або використовуючи спеціальні статистичні пакети або функції для лінійної моделі з (п–2) ступенями вільності і з надійністю p=1- знайдемо t_(p,n-2)

Якщо значення│t_{розр. і}│<t_(p,n-2)., з надійністю p ми можемо стверджувати, що оцінка b_i є статистично незначимою, тобто ми приймаємо нуль-гіпотезу (Н₀: ) і робимо висновок, що значення b_i у виборці є несуттєве, випадкове.

У протилежному випадку приймаємо альтернативну гіпотезу Н_i: .

Фактичне значення t – критерію для коефіцієнта регресії b₁ можна отримати, якщо витягнути квадратне коріння із знайденого раніше F – критерію:

Для того, щоб визначити, як же параметри b₀ і b₁ пов’язані з параметрами , потрібно побудувати інтервали довіри.

Процедура побудови інтервалів довіри є аналогічною до процедури тестування значимості знайдених параметрів простої вибіркової лінійної регресії

Для перевірки значимості коефіцієнта кореляції також використовуємо t – критерій Ст'юдента.

Сформулюємо нуль-гіпотезу: Н₀:, тобто в генеральній сукупності між факторами x і y немає лінійного зв’язку, та альтернативна гіпотеза: Н₀:.

Розрахуємо значення

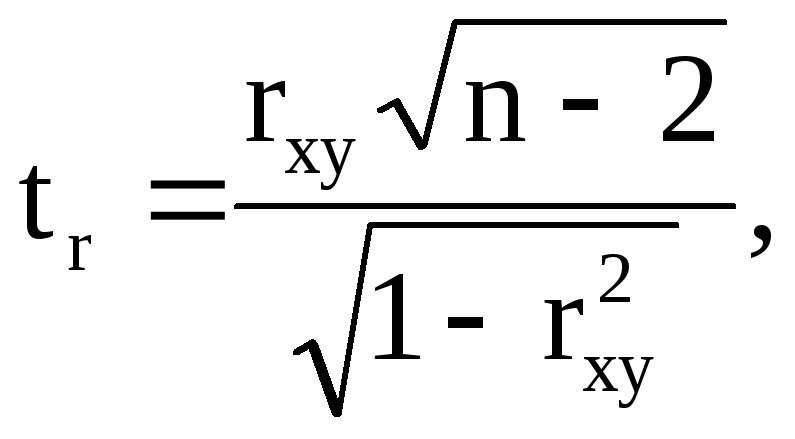
де r_xy – вибірковий лінійний коефіцієнт кореляції між х і у;

n – кількість спостережень.

Величина t_r розподілена за t – розподілом Ст’юдента з (п–2) ступенями вільності.

Розраховане значення t для лінійної моделі порівняємо з критичним значенням t_{(p, n-2)} з надійністю р її (n–2) ступенями вільності Якщо t>t_{(p, n-2)} відкидаємо нуль-гіпотезу Н₀: ρ=0 і приймаємо гіпотезу Н₁:, тобто вибірковий коефіцієнт кореляції є достовірним.

Формула свідчить, що в парній лінійній регресії .

Таким чином, перевірка гіпотези про значимість коефіцієнтів кореляції і регресії рівносильна перевірці гіпотезі про адекватність (суттєвість) лінійної моделі.

У прогнозних розрахунках за рівнянням регресії визначається значення, що передбачається, як точковий прогноз при заданому x_pr, тобто підставляючи це значення в рівняння регресії . Але точковий прогноз не завжди може бути дійсним, тому він доповнюється стандартною помилкою , тобто , і відповідною інтервальною оцінкою прогнозного значення (інтервалом довіри для прогнозного значення):

,

де .

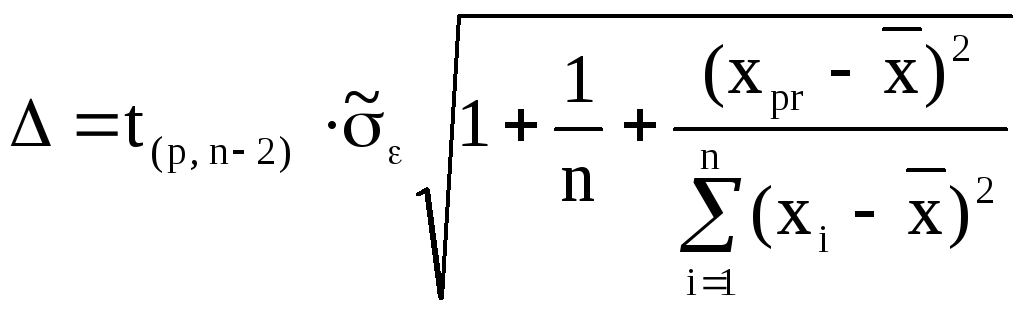На практиці більше застосовується побудова інтервалів довіри для математичного сподівання значення , тобто побудова інтервалів довіри для =₀+₁·x_pr:

, де

Розглянута формула стандартної помилки середнього значення , що прогнозується при заданому значенні x_p , характеризує помилку положення лінії регресії. Ця величина досягає мінімуму, якщо , і зростає, у міру того, як віддаляється від середнього значення x в любому напрямку. Інакше кажучи, чим більш різниця між x_pr і , тим більш помилка , з якою прогнозується середнє значення y для заданого значення x. Можна очікувати найкращі результати прогнозу, якщо ознака-фактор x знаходиться в центрі області спостережень x і неможливо очікувати хороших результатів прогнозу при віддаленні x_pr від . Якщо значення x_pr виявляється за межами спостережуваних значень x, що використовуються при будуванні лінійної регресії, то результати прогнозу погіршуються в залежності від того, наскільки x_pr відхиляється від області спостережуваних значень фактору x.

Довірча зона базисних даних для лінійної регресії знаходиться за формулами: