Лекция№2 МОЯ

1. Работа сил электростати ческого поля

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда q из одной точки электрического поля в другую на отрезок пути dx , по определению, равна dA = F dx = q₀ Edx.

[а — угол между F и направлением движения].

Если работа совершается внешними силами, то dA < 0, если силами    поля, то dA > 0. Интегрируя последнее выражение, получаем, что работа против сил поля при перемещении q₀ из точки а в точку b

A = F dx …

[F = q₀ E — кулоновская сила, действующая на пробный заряд q₀ в каждой точке поля с напряженностью E].

Тогда работа

Докажем, что работа, совершаемая при перемещении заряда в электрическом поле, зависит только от начального и конечного положений заряда.

Пусть пробный заряд q₀ перемещается в поле заряда Q из точки а, удаленной от Q (на расстояние r₁ , в точку Ь, удаленную от Q на расстояние г₂, по пути аа'b (рис. ). Работа на участке аа' не производится, так как перемещение совершается перпендику-лярно вектору Е. Следовательно, работа переноса пробного заряда q₀ от а к b равна

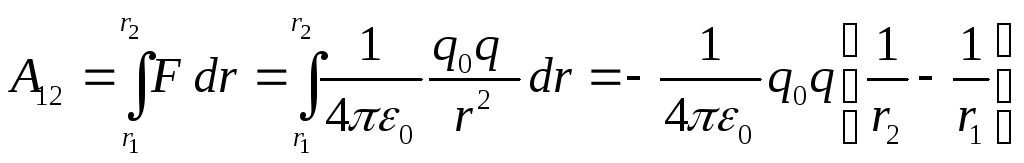
Работа сил электрического поля при перемещении заряда не зависит от формы пути, а зависит лишь от взаимного расположения начальной и конечной точек траектории.

Это свойство потенциальных полей, Из него следует, что работа, совершаемая в электрическом поле по замкнутому контуру, равна нулю (3.25)

При перемещении зарядов изменяется их взаимное расположение, поэтому работа, совершаемая электрическими силами, в этом случае равна изменению потенциальной энергии перемещаемого заряда: А = - ∆П

Это утверждение справедливо как для однородного, так и для неоднородного поля.

2. Потенциал поля

Энергетическая характеристика поля

Выберем в электрическом поле какую-либо точку за начальную и будем вести от нее отсчет потенциальной энергии. Для перемещения заряда из начальной точки в данную точку поля при любой форме пути должна быть затрачена одна и та же работа А. Поэтому в любой точке поля потенциальная энергия П заряда численно равна работе, которую необходимо совершить для перемещения заряда в эту точку.

Подобно тому, как потенциальная энергия в поле сил тяготения пропорциональна массе тела, потенциальная энергия электрического поля пропорциональна заряду: П = φQ

Вёличину φ =П /Q называют электрическим потенциалом поля.

Единица электрического потенциала — вольт(В).

Она характеризует потенциальную энергию, которой обладал бы положительный единичный заряд, помещенный в данную точку поля.

Дпя того чтобы вычислить полную потенциальную энергию заряда, надо найти работу сил поля по перемещению заряда из данной точки по- ля в точку, где поле отсутствует, например на бесконечно большое рас- стояние от зарядов, создающих поле.

В соответствии с (3 .26) работа сил поля может быть вычислена через разность потенциалов начальной и конечной точек траектории: А = - ∆П =-(П₂ – П₁ ) = Q (φ₁ – φ₂ )

Веллчину (φ₁ – φ₂ ) называют разностью потенциалов электрического поля. Понятие разности потенциалов (или напряжения) применимо лишь к двум различным точкам поля.

Потенциал является энергетической характеристикой электрического поля и как скалярная величина может принимать положительные или отрицательные значения. Следует обратить внимание, что физический смысл имеет разность потенциалов, так как через нее выражается работа сил поля по перемещению заряда. Говоря о потенциале в данной точке поля, всегда подразумевают разностъ потенциалов, имея в виду, что одна из точек выбрана заранее и находится в бесконечности. Так как потенциальная энергия зависит от выбора нулевого уровня энергии, то потенциал может бьтъ определен лишь по отношению к некоторому уровню, принятому за нулевой.

Выбор точки с нулевым потенциалом обычно определяется в зависимости от условий задачи. При решении задач целесообразно полагать равным нулю потенциал Земли, а не бесконечно удаленных точек электрического поля. Выбор нулевого уровня потенциала не влияет на значе ние разности потенциалов.

При решении задач часто необходимо знать потенциал электрического поля точечного заряда Q в точке, удаленной на расстояние r от заряда: φ =

Эта формула справедлива при условии, что потенциал стремится к нулю при r → ∞ .

Эквипотенциальные поверхности

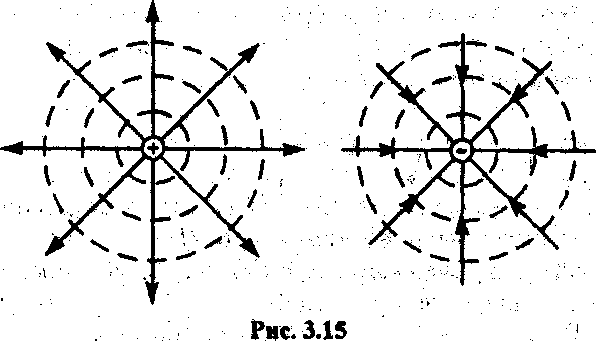
. Графически электрическое поле можно изображать не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей — совокупностей точек, имеющих одинаковый потенциал. Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности дают эквипотенциальные линии.

На рис. 3,15 показаны эквипотенциальные линии поля точечного заряда, потенциал которого

Эквипотенциалъные линии представляют собой концентрические окружности, эквипотенциалъные поверхности. — концентрические сферы. Из рисунка видно, что линии напряженности (радиальные лучи) перпендикулярны эквипотенциальным линиям. Покажем, что линии напряженности всегда перпендикулярны эквипотенциальным поверхностям. Определим работу по перемещению заряда вдоль эквипотенциальной поверхности из точки 1 в точку 2 (рис. 3.16):

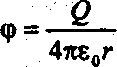
с другой етороны, А =

Так как –ф₁ = ф₂, то работа по перемещению заряда по эквипотенциальной поверхности равна нулю, т, е. = 0. Так как Q , Е, а: отличны от нуля,то

Таким образом, вектор напряженности Е электростатического поля всегда перпендикулярен поверхности равного потенциала.

Эквипотенциальных поверхностей вокруг системы зарядов можно провести бесчисленное множество. Но для наглядного представления о том, как изменяется разность потенциалов в данном поле, их проводят таким образом, чтобы разность потенциалов двух любых соседних линий была одна и та же, например 1 В. Тогда густота эквипотенциальных линий наглядно характеризует напряженность поля; там, где эти линии расположены гуще, напряженность поля больше. Зная расположение эквипотенциальных линий (поверхностей), можно построить линии напряженности или по известному расположению линий напряженности можно построить эквипотенциальные поверхности.