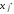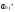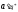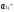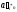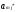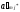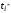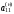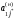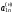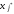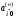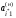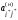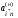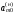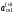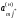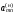Ye_Yu_Dorohina_M_A_Halikov_-_Modelirovanie_m
.docx2.4.Алгебра симплекс-метода
Последующий материал, посвященный анализу оптимального решения в задаче Канторовича, существенно использует симплекс-процедуру перехода от начального допустимого базисного решения к оптимальному решению. В связи с этим обстоятельством представляется необходимым напомнить табличный метод нахождения оптимального решения в задаче линейного программирования. Среди множества реализаций симплекс-процедуры выберем ту, которая, во-первых, в явном виде разделяет базисные и свободные переменные и позволяет в последней симплекс-таблице выделить так называемую матрицу эффективности, а во-вторых, хорошо приспособлена для решения на ЭВМ.
В качестве примера рассмотрим простейшую модель оптимизации производства по критерию максимума дохода в случае, когда для производства j-й продукции используется один технологический способ производства Тj ( j = 1,2,..., n). Пусть рj — доход от реализации продукции, изготовляемой однократным применением j-й технологии. Тогда вектор “выпуск-затраты”, описывающий j-й производственный способ имеет вид Рj =( рj ; a1j , a2j ,..., aij ,..., anj), где aij — затраты i-го ресурса ( i =1,2,..., т) при однократном применении j-й технологии. Будем считать, что затраты исчисляются в стоимостном выражении. Таким образом, каждая компонента вектора Рj суть стоимость или затрачиваемых производственных факторов, или произведенной продукции.
Состояние
производственной системы задается
вектором
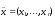 интенсивностей
использования технологий Т1,...,
Тn.
интенсивностей
использования технологий Т1,...,
Тn.
Вектор
“выпуск-затраты”, описывающий
функционирование производственной
системы, имеет вид
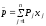 .
При этом выпуск товарной продукции
равен
.
При этом выпуск товарной продукции
равен
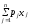 ,
а затраты i-го
ресурса составляют величину
,
а затраты i-го
ресурса составляют величину
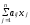 .
.
Если целью функционирования производственной системы является максимизация выпуска товарной продукции, то модель производственной системы представляется в следующем виде:
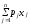
max;
(2.7)
max;
(2.7)
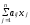
bi
(i=1,2,...,
m);
(2.8)
bi
(i=1,2,...,
m);
(2.8)
хj 0 (j=1,2,..., n). (2.9)
Задача нахождения оптимального состояния производственной системы в данном случае является задачей линейного программирования.
Пусть
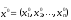 — одно из решений задачи линейного
программирования. В этом случае наибольшая
величина выпуска определяется числом
— одно из решений задачи линейного
программирования. В этом случае наибольшая
величина выпуска определяется числом
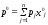 .
.
Для
нахождения оптимального решения
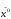 в задаче (2.7)-(2.9) приведем систему
ограничений модели к каноническому
виду. Для этого ограничения (2.8), (2.9)
превратим в уравнения, введя переменные
ti
,
экономический смысл которых — количество
неиспользованных ресурсов вида i
:
в задаче (2.7)-(2.9) приведем систему
ограничений модели к каноническому
виду. Для этого ограничения (2.8), (2.9)
превратим в уравнения, введя переменные
ti
,
экономический смысл которых — количество
неиспользованных ресурсов вида i
:
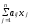 +
ti
=bi
(i=1,2,...,
m).
(2.10)
+
ti
=bi
(i=1,2,...,
m).
(2.10)
Задача линейного программирования (2.7), (2.10), (2.9) с дополнительными ограничениями на неотрицательность переменных ti имеет размерность n + m. При этом число базисных переменных в случае линейной независимости системы ограничений (2.8) равно числу ограничений, т.е. m, а число свободных переменных совпадает с числом неизвестных в линейной форме (2.7), т.е. равно n. Обозначим через с значение целевой функции в форме (2.7).
В исходном опорном плане задачи будем считать переменные группы ti базисными переменными, а группы xj — свободными. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу линейного программирования (2.7),(2.10), (2.9) в следующем виде:
с
=
0 -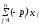
max;
(2.11)
max;
(2.11)
ti
= bi
-
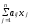 , ti
(i=1,2,...,
m);
(2.12)
, ti
(i=1,2,...,
m);
(2.12)
хj 0 (j=1,2,..., n). (2.9)
Задача (2.11), (2.12), (2.9) может быть представлена следующей матрицей коэффициентов при переменных:
 .
(2.13)
.
(2.13)









В матрице (2.13) коэффициенты первой строки совпадают с коэффициентами линейной формы (2.11): a00 = 0, a01 = - p1 ,..., a0n = - pn , а коэффициенты первого столбца — с коэффициентами правых частей ограничений (2.8): a10 = b1 ,..., ai0 = bi ,..., am0 = bm.
По виду коэффициентов матрицы (2.13) легко судить, является ли найденное базисное решение допустимым и, если оно допустимо, то будет ли оптимальным. Действительно, замечая, что столбец коэффициентов ai0 , i представляет собой базисное решение, соответствующее базису t1,..., tm , а строка коэффициентов a0j , j представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении для с, приходим к выводу, что базисное решение, соответствующее базису t1,..., tm , допустимо если ai0 (в нашем случае это действительно так: ai0 = bi ). Если, кроме того, a0j , то это базисное решение является и оптимальным, так как линейная форма (2.11) принимает наибольшее значение, равное a00 , при равенстве нулю свободных переменных (в нашем случае это условие не выполняется, так как все элементы первой строки матрицы (2.13) неположительны). Таким образом, матрица (2.13) соответствует допустимому базисному решению, но не оптимальному.
Итерационную симплекс-процедуру начнем с первой таблицы, представленной коэффициентами матрицы (2.13), где переменные по строкам соответствуют базисным переменным, а по столбцам — свободным.
Среди
отрицательных коэффициентов первой
строки выделим наибольший по абсолютной
величине, а если таких окажется несколько,
то любой из них. Пусть этот коэффициент
соответствует свободной переменной
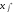 .
Теперь необходимо
.
Теперь необходимо
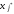 перевести
в базис, заменив в нем некоторую переменную
группы ti
.
Определим, какую из базисных переменных
следует сделать свободной. Очевидно,
ту, которая быстрее обратится в нуль
при увеличении
перевести
в базис, заменив в нем некоторую переменную
группы ti
.
Определим, какую из базисных переменных
следует сделать свободной. Очевидно,
ту, которая быстрее обратится в нуль
при увеличении .
Это будет та базисная переменная
.
Это будет та базисная переменная
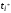 ,
для которой коэффициент в j*-ом
столбце
,
для которой коэффициент в j*-ом
столбце
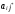
0 и отношение
0 и отношение
 наименьшее.
Столбец и строку, соответствующие
свободной переменной
наименьшее.
Столбец и строку, соответствующие
свободной переменной
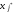 и
базисной
и
базисной
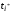 отметим в первой (очередной) симплекс-таблице
двойными линейками. Последующие
преобразования очередное симплекс-таблицы
представлены в табл.2.2.
отметим в первой (очередной) симплекс-таблице
двойными линейками. Последующие
преобразования очередное симплекс-таблицы
представлены в табл.2.2.
Таблица 2.2
|
|
1 |
х1 |
... |
|
... |
хn |
|
c |
a00 a00 |
a01 a01 |
... |
|
... |
a0n a0n |
|
t1 |
a10 a10 |
a11 a11 |
... |
|
... |
a1n a1n |
|
... |
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
... |
|
|
... |
... |
... |
... |
... |
... |
... |
|
tm |
am0 am0 |
am1 am1 |
... |
|
... |
amn amn |
В
табл.2.2 в левом верхнем углу каждой
клетки находятся коэффициенты aij
предыдущей симплекс-таблицы (в нашем
случае — первой), а коэффициенты aij,
которыми мы заполнили нижние углы,
соответствуют пересчету коэффициентов
матрицы ограничений (2.12) в связи с тем,
что мы заменяем базисную переменную
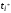 на
свободную
на
свободную
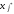 .
.
Коэффициенты aij получаем по следующим правилам:
1)
коэффициент на пересечении отмеченных
строки и столбца
 :
:
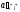 = 1/
= 1/
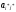 ;
;
2)
в клетках выделенной строки записываем
верхние коэффициенты, умноженные на
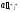 :
:
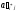 =
=
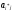
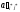 для
j
=
0,1, ..., j
*- 1, j
*+ 1,..., n;
для
j
=
0,1, ..., j
*- 1, j
*+ 1,..., n;
3)
в клетках выделенного столбца записываем
верхние коэффициенты, умноженные на
-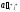 :
:
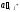 =
=
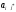
(-
(- )
для
i
=
0,1,..., i
*- 1, i
*+ 1,..., m;
)
для
i
=
0,1,..., i
*- 1, i
*+ 1,..., m;
4)
в клетках выделенной строки отмечаем
особым способом верхние коэффициенты
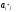 (кроме
(кроме
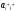 ),а
в клетках выделенного столбца — нижние
коэффициенты
),а
в клетках выделенного столбца — нижние
коэффициенты
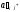 (кроме
(кроме
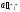 );
);
5)
в остальных клетках записываем
произведение выделенных особым способом
коэффициентов, на пересечении которых
стоит данная клетка:
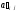 =
=
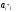
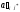 для
i
=
0,1,..., i
*- 1, i
*+ 1,..., m
и j
=
0,1,..., j
*- 1, j
*+ 1,..., n.
для
i
=
0,1,..., i
*- 1, i
*+ 1,..., m
и j
=
0,1,..., j
*- 1, j
*+ 1,..., n.
Затем
переходим к заполнению таблицы 2.3,
которая отличается от табл.2.2 тем, что
отмеченная свободная переменная
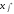 стала
базисной, а отмеченная базисная переменная
стала
базисной, а отмеченная базисная переменная
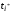 стала свободной.
стала свободной.
Таблица 2.3.
|
|
1 |
х1 |
... |
|
... |
хn |
|
c |
|
|
... |
|
... |
|
|
t1 |
|
|
... |
|
... |
|
|
... |
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
... |
|
|
... |
... |
... |
... |
... |
... |
... |
|
tm |
|
|
... |
|
... |
|
Верхние левые клетки табл.2.3 (новые значения коэффициентов aij) заполняются по следующим правилам:
1)
строка и столбец, соответствующие новым
базисной (i*-я
строка) и свободной ( j*-й
столбец) переменным, заполняются нижними
коэффициентами выделенных строк и
столбца табл.2.2:
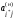 =
=
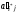 для j
=
0,1,..., n
и
для j
=
0,1,..., n
и
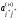 =
=
 для
i
=
0,1,..., m.
для
i
=
0,1,..., m.
2)
в остальные клетки записываются суммы
коэффициентов, стоящих в соответствующих
клетках табл.2.2:
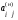 =
=
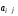 +
+
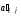 для i
=
0,1,..., i
*- 1, i
*+ 1,..., m
; j
=
0,1,..., j
*- 1, j
*+ 1, ..., n.
для i
=
0,1,..., i
*- 1, i
*+ 1,..., m
; j
=
0,1,..., j
*- 1, j
*+ 1, ..., n.
Заполненная
таким образом табл.2.3 соответствует
матрице коэффициентов (2.13) при новом
составе базисных и свободных переменных.
Отметим попутно, что a00
,
так как a00
является
произведением положительных чисел
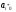 (в силу допустимости предыдущего
базисного решения) и
(в силу допустимости предыдущего
базисного решения) и
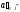 (в силу процедуры выбора
j*
столбца и правила формирования
коэффициента
(в силу процедуры выбора
j*
столбца и правила формирования
коэффициента
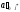 ).
Следовательно,
).
Следовательно,
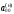
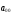 и значение целевой функции с,
соответствующее табл.2.3, выше значения,
полученного в табл.2.2. Далее вся процедура
повторяется до момента, когда на очередном
шаге получается оптимальное решение.
и значение целевой функции с,
соответствующее табл.2.3, выше значения,
полученного в табл.2.2. Далее вся процедура
повторяется до момента, когда на очередном
шаге получается оптимальное решение.
В качестве числового примера, иллюстрирующего табличный метод нахождения оптимального решения в задаче линейного программирования рассмотрим производственную систему с линейным технологическим множеством, использующую три основных производственных способа: Р1 = (1; 2,1), Р2 = (3; 1,2) и Р3 = (3; 3,1). Для определенности затрачиваемые факторы будем интерпретировать как “труд” и “капитал”. В этом случае способ Р3 наиболее трудоемкий, а Р2 — капиталоемкий. Предположение о линейности технологического множества определяет в качестве последнего трехгранный конус в пространстве Р3 (“выпуск-затраты”):
Т = (с, L, K) x1 0; x2 0; x3 0; c = x1 + 3 x2 + 3 x3,
L = 2x1 + x2 + 3 x3, К = x1 + 2x2 + x3.
Модель производственной системы представим в следующем виде:
c = x1 + 3 x2 + 3 x3 max; (2.14)
2x1 + x2 + 3 x3 L; (2.15)
x1 + 2x2 + x3 K; (2.16)
x1 0; x2 0; x3 0. (2.17)
Пусть объем фактора L равен 8 единицам, а фактора К — 4 единицам. В этом случае, в ходе решения соответствующей оптимизационной задачи осуществляется выбор интенсивностей использования технологических способов Р1, Р2 и Р3, при которых достигается наибольший выпуск товарной продукции при условии использования факторов “труд” и “капитал” в объеме не превосходящем их наличного количества (8,4).
Приведем краткое решение задачи (2.14)-(2.17).
Ограничения (2.15),(2.16) превратим в уравнения, введя переменные t1 0, t2 0, экономический смысл которых — количество неиспользованных ресурсов соответственно вида L и К . При этом получим систему ограничений:
2x1 + x2 + 3 x3 + t1 = 8; (2.18)
x1 + 2x2 + x3 + t2 = 4. (2.19)
Задача (2.14), (2.17), (2.18), (2.19) с дополнительными ограничениями t1 0, t2 0 является задачей линейного программирования размерности 5, у которой число базисных переменных равно 2 (соответствует числу актуальных ограничений), а число свободных переменных равно 3. Принимая x1 , x2 и x3 за свободные переменные, приведем задачу к следующему виду:
c
=
0 - (-x1
-
3
x2
- 3
x3)
max;

t1
= 8- (2x1
+
x2
+ 3
x3
);
(2.20) 
t2 = 4x1 + 2x2 + x3;
x1
0; x2
0;
x3
0;
t1
0; t2
0.
Так как решаемая задача — задача на максимум, то соотношения (2.20) показывают, что начальное базисное решение является допустимым, но не оптимальным (коэффициенты при x1 , x2 и x3 в выражении для с не являются неотрицательными числами).
В ходе последовательного преобразования таблиц коэффициентов, используя симплекс-процедуру, получим оптимальное решение задачи (2.14), (2.18), (2.19), (2.17), исходя из начального допустимого решения (2.20).
Таблица 2.4(а)
|
|
|
1 |
x1 |
x2 |
x3 |
|
|
с |
0 6 |
-1 3/2 |
-3 3/2 |
-3 3/2 |
|
|
t1 |
8 -2 |
2 -1/2 |
1 -1/2 |
3 -1/2 |
|
|
t2 |
4 2 |
1 1/2 |
2 1/2 |
1 1/2 |
Таблица 2.4(б)
|
|
|
1 |
x1 |
t 2 |
x3 |
|
|
с |
6 18/5 |
1/2 9/10 |
3/2 -3/10 |
-3/2 3/5 |
|
|
t1 |
6 12/5 |
3/2 3/5 |
-1/2 -1/5 |
5/2 2/5 |
|
|
x 2 |
2 -6/5 |
1/2 -3/10 |
1/2 1/10 |
1/2 -1/5 |
Таблица 2.4(в)
|
|
|
1 |
x1 |
t 2 |
t 1 |
|
|
с |
48/5
|
19/10
|
6/5
|
3/5
|
|
|
x3 |
12/5
|
3/5 3/5 |
-1/5
|
2/5
|
|
|
x2 |
4/5
|
1/5
|
3/5
|
-1/5
|