Колебания и волны

Гармонические колебания.

Гармоническими называются колебания, в которых величина х изменяется по закону

, (1)

где а – амплитуда, - фаза,  - начальная фаза, _o - циклическая частота, _o=2 . Период колебаний T , а также частоты ν и ₀ связаны:

. (2)

Обратите внимание! Циклическая и обычная частоты имеют разные наименования единиц измерения: [] = c^-1, []=Гц.

Продифференцировав (1) по времени, найдем скорость и ускорение

; ) (3)

Графики на рис.1 показывают, что х и находятся в противофазе, а скорость опережает смещение х на .

NB! Наиболее часто встречающее заблуждение учащихся состоит в том, что они думают, что на рис.1 изображена траектория. НЕТ! Это графики! Зависимости х (и производных) от времени! Притом при нулевой начальной фазе и одинаковых по масштабу амплитудах! Движение одномерное! Поэтому траектория – набор отрезков вдоль вертикальной оси х.

Дифференциальное уравнение гармонического осциллятора. Выражения для смещения х и ускорения отличаются только коэффициентом при cos (…). Поэтому =, или

(4)

Это и есть дифференциальное уравнение гармонического осциллятора. Функция (1) - общее решение этого уравнения. Оно содержит две произвольные константы а и . Их можно найти из начальных условий, например, если даны смещение и скорость в начальный момент t=0:

; .

Что же такое гармонический осциллятор? Ответ очевиден: кто меняет свою единственную координату по уравнению (1) или (4) – тот и есть гармонический осциллятор. Простейшими примерами гармонических осцилляторов являются грузик на пружинке, математический маятник, физический маятник. И пример для гурманов – вертикальные колебания льдины на воде. Попробуйте понять, что между этими примерами общего.

Грузик на пружине (пружинный маятник). Пусть грузик массы m подвешен на невесомой пружине жесткостью k. Смещение х будем отсчитывать от положения равновесия (рис.2). В состоянии равновесия пружина растянута под действием силы тяжести mg груза настолько, чтобы сила упругости была в точности равна -mg. Поскольку эти постоянные силы равны и противоположно направлены, они в сумме всегда равны нулю. В процессе колебаний сила упругости будет состоять из двух частей: (1) постоянной составляющей равной mg и (2) переменной составляющей равной kx. Таким образом, в записи второго закона Ньютона для грузика можно не учитывать силу тяжести mg и постоянную составляющую силы упругости (равную -mg) . Тогда произведение массы на ускорение равно переменной составляющей силы упругости

. (5)

Редкий ученик понимает, почему справа минус. Возьмите пружинку (хоть из авторучки) и попробуйте её растянуть и сжать. Что Вы заметили? Когда пружину сжимают, она стремится распрямиться (смещение вверх, сила упругости вниз), а когда растягивают, она стремится сжаться (смещение вниз, сила упругости вверх). Таким образом, знаки смещения x и силы kx всегда противоположны, поэтому и минус. Теперь перенесем - kx влево и разделим уравнение (5) на m

.

Правда, похоже на (4)? Чтобы сходство стало полным, обозначим . Тогда мы получим , т.е. дифференциальное уравнение гармонического осциллятора (ГО).

Мораль: коэффициент при x в дифференциальном уравнении гармонического осциллятора равен квадрату циклической частоты этого осциллятора. Если конечно Вы не забыли все уравнение предварительно разделить на коэффициент при ! А чему же равно x? Раз получено уравнение, идентичное дифференциальному уравнению (4), (1) - его общее решение.

Пора спросить: а все ли знают, что точка над x обозначает первую производную по времени от x? Теперь догадайтесь, что означают две точки над x. И начинайте читать все сначала.

Из равенства следует, что циклическая частота пружинного маятника, зависит от жесткости пружины и массы груза: чем жестче пружина – тем больше частота, чем больше масса груза, тем меньше частота. С периодом все наоборот:

; . (6)

Пример из министерского тестирования: во сколько раз увеличится период колебаний пружинного маятника, если его массу и жесткость пружины увеличить в 2 раза? Ответ: не изменится. А если массу увеличить в 8 раз, а жесткость пружины увеличить в 2 раза? Ответ: в два раза. И так далее.

Ф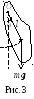изический маятник. Это твердое тело, совершающее малые колебания относительно неподвижной оси О, перпендикулярной листу (рис. 3). Запишем основное уравнение динамики вращательного движения в проекции на ось вращения О

(7)

(слева произведение момента инерции I на угловое ускорение, справа – момент силы тяжести). Чтобы понять, откуда справа минус, вспомним, куда направлены угловое ускорение и момент силы mg. Правильно, оба вектора вдоль оси вращения. А почему всегда в разные стороны? Спрошу на экзамене! Разделим обе части на I; учтем, что для малых углов ; перенесем все в левую часть, обозначим и получим опять дифференциальное уравнение гармонического осциллятора

, (8)

Только роль смещения вместо x выполняет угол φ. Решение уравнения (8) также совпадает с формулой (1) с точностью до обозначений: , где для разнообразия амплитуда обозначена φ₀. Циклическая частота и период колебаний физического маятника равны

; . (9)

Такую же частоту и период имеет математический маятник длины l_пр=, которую называют приведенной длиной физического маятника.

Математический маятник - это частица массы m, совершающая малые колебания на нити длиной l (в плоскости листа - на рис.4). Основное уравнение динамики вращательного движения будет отличаться только тем, что момент инерции частицы известен (),  ; Откуда минус? Да оттуда же! Теперь разделим обе части на ml²; учтем, что для малых углов ; перенесем все в левую часть и получим что? Опять дифференциальное уравнение гармонического осциллятора (8), где на этот раз ,  циклическая частота и период колебаний математического маятника равны

; . (10)

Похоже на выражения (6 и 9), но есть и различие: период (и обе частоты) математического маятника не зависят от его массы! А зависят только от g! Отсюда простейший способ измерения ускорения свободного падения g. Берем нить известной длины с грузиком и измеряем период его колебаний. Подставляем в (8) и находим g.

Пример из министерского тестирования: во сколько раз увеличится период колебаний математического маятника, если его массу увеличить в 2 раза и длину нити увеличить в 2 раза? Ответ: в . А если массу увеличить в 8 раз, а длину нити увеличить в 4 раза? Ответ: в 2 раза. И масса в обоих случаях не при чем!

Мораль. Свободные колебания любого осциллятора без трения будут гармоническими, если действующая сила направлена к положению равновесия и пропорциональна смещению от положения равновесия. В примере со льдиной именно так и получается: при вертикальных колебаниях меняется погруженная в воду часть льдины, а  и сила Архимеда пропорциональная глубине погружения.

Сложение гармонических колебаний одного направления. Можно условно изображать колебания с помощью вектора амплитуды , вращающегося с угловой скоростью  против часовой стрелки, так как проекции этого вектора изменяются по гармоническому закону. Действительно, угол вектора с осью х в момент времени t равен , а его проекция на ось х равна аcos. Проекция вектора суммы двух векторов равна сумме однонаправленных гармонических колебаний. Такой способ называется векторной диаграммой. Мы рассмотрим два случая: 1- когда частоты складываемых колебаний равны, 2 - когда они мало отличаются.

NB! Термины “мало- много” требуют обязательного уточнения: по сравнению с чем? Всем известно, что три волоса на голове – это мало, а в тарелке – много! В нашем случае (колебаний, а не волос) уточнение состоит в том, что разность складываемых частот много меньше каждой из них. Обязательно обращайте внимание на уточнение! Оно неизбежно будет использовано при выкладках. Так, мы недавно использовали (дважды!) термин малые колебания. А уточнение состояло в том, что для них .

1 Пусть складываются гармонические колебания х₁ и х₂ с одинаковой частотой . Тогда результирующее смещение равно

x= х₁ + х₂ = а₁ cos+ а₂ cos=.

Изобразим колебания векторами и , которые в начальный момент составляют с осью х углы ₁ и ₂ соответственно (рис.5). Амплитуду а и начальную фазу  результирующего колебания можно найти, как видно из рисунка, из соотношений

(11)

(12)

Из формулы (11) видно, что амплитуда результирующего колебания существенно зависит от разности фаз . При сложении синхфазных колебаний (т.е. таких, что =0) результирующая амплитуда максимальна, а при сложении колебаний в противофазе - минимальна:

; .

2 Пусть и ₂. Это значит, частоты мало отличаются! В этом случае справедлив рис.5. Но теперь векторы и вращаются с немного отличающимися угловыми скоростями, модуль результирующего вектора будет медленно (почему?,- спрошу!) изменяться от до , причем сам вектор вращается с угловой скоростью, близкой к и ₂. Строго говоря, результирующее колебание не является гармоническим. Его можно рассматривать, как почти гармоническое, но с медленно периодически изменяющейся амплитудой (рис.6). Такие колебания называются биениями. Результирующая амплитуда также может быть выражена формулой (11), но теперь разность фаз следует заменить выражением  = - = + .

Сложение взаимно перпендикулярных колебаний. Рассмотрим несколько случаев.

1. Пусть складываются гармонические колебания х и y с одинаковой частотой 

и . (13)

Поскольку cos любого угла можно записать, как sin дополнительного (до 90⁰) угла, то выражение для y можно представить как , где +=90⁰. Перепишем выражения (13) в виде

; (14)

Е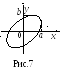сли возвести оба уравнения в квадрат, расписать синус суммы, сложить уравнения и учесть что sin²…+ cos²… =1, то можно исключить время. Так получим уравнение уравнение траектории - эллипс (рис.7). Обязательно получите самостоятельно! По этой эллиптической траектории точка будет вращаться с частотой . Рассмотрим частные случаи.

а) =0. Тогда . Эллипс вырождается в наклонный отрезок в первом и третьем квадрантах (рис.8а). Точка будет гармонически колебаться вдоль этого отрезка с частотой .

б) =. Тогда . Тоже отрезок, только во втором и четвертом квадрантах (рис.8 б).

в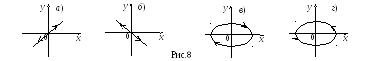) =/2. Тогда получим ,  частица движется по эллипсу, полуоси которого совпадают с осями координат (рис.8 в). Так как колебание y опережает колебания х на /2 (см. формулы (14)!), то y достигает max раньше, чем х, - поэтому вращение происходит по часовой стрелке.

г) =3/2=(-/2);  наоборот: колебание х опережает колебания y на /2,  тоже вращение по эллипсу, только против часовой стрелки (рис.8 г).

2. Если частоты взаимно перпендикулярных колебаний отличаются в целое число раз, то траектория результирующего колебания представляет собой довольно сложную кривую. Эти кривые называются фигурами Лиссажу.

Затухающие колебания.

Дифференциальное уравнение затухающих колебаний. В реальной колебательной системе всегда есть силы типа трения, которые приводят к уменьшению амплитуды (и энергии) колебаний. Тогда свободные колебания называются затухающими. Пусть на частицу массы m кроме квазиупругой силы (-kx) действует сила сопротивления, пропорциональная скорости . Тогда уравнение второго закона Ньютона будет иметь вид . Перенесем все в левую часть, разделим на m и введем обозначения: ; ; после чего получим

. (15)

Циклическую частоту ₀ называют собственной частотой,  - коэффициентом затухания. Уравнение (15) - это дифференциальное уравнение затухающих колебаний. Его решение

, (16)

где а₀ и  - произвольные константы, которые можно найти из начальных условий; Частота затухающих колебаний , а зависит от :

. (17)

С

Рис.9

трого говоря, затухающие колебания не являются гармоническими (рис.9), но их можно условно называть гармоническими с экспоненциально уменьшающейся амплитудой (пунктир на рис.9). Решение (16) имеет смысл, если . В противном случае в (17) под корнем стоит отрицательная величина и процесс затухает апериодически. Физически это означает, что трение слишком велико, чтобы происходили колебания, хотя бы и с уменьшающейся амплитудой.

Время релаксации – это время , за которое амплитуда колебаний уменьшается в е раз.

Так как меньше а_о в е раз, то ,  -1=-,  .

Логарифмический декремент затухания – это логарифм отношения двух последовательных амплитуд

.

Подставляя в =1/, получим =Т/ ,   - величина, обратная такому числу колебаний, за которое амплитуда уменьшится в е раз!

Вынужденные колебания.

Дифференциальное уравнение вынужденных колебаний. Вынужденные колебания можно получить, если к перечисленным выше силам (квазиупругой = - kx и трения=) добавить внешнюю силу, например, периодическую F=F₀cost. Тогда по второму закону Ньютона

или

, (18)

где ; ; . Общее решение неоднородного дифференциального уравнения (18) состоит из суммы общего решения однородного уравнения (15) и частного решения неоднородного (18). Общее решение однородного ДУ, как мы видели, затухает со временем. Поэтому остается только частное решение (соответствующее установившимся колебаниям), которое показывает, что в системе устанавливаются гармонические колебания с частотой  вынуждающей силы, но отстающие от нее по фазе на некоторое φ

. (19)

Если дважды продифференцировать (последний раз предупреждаю, что это значит – два раза взять производную!) уравнение (18), нарисовать векторную диаграмму с учетом сдвига фаз, то можно найти а и φ

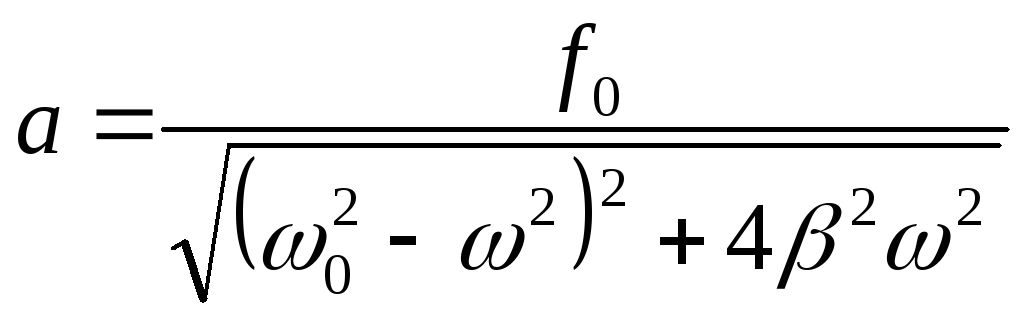
, (20)

Резонанс. Первая из формул (20) показывает зависимость амплитуды а от частоты вынуждающей силы (рис.10). При =0, а=, а максимум амплитуды соответствует условию . Но еще проще найти минимум только для выражения под корнем, приравняв нулю производную от него. Соответствующая частота _рез называется резонансной

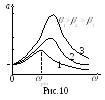_рез=, (21)

а само явление достижения максимальной амплитуды называется резонансом. Подставляя в первую из формул (20) резонансную частоту (21), получим максимальную амплитуду

. (22)

Из (22) и рис.10 видно, что чем меньше затухание в системе, тем ярче выражен резонанс. Резонанс используют, если нужно усилить колебания, и, наоборот избегают, если он может привести к нежелательному усилению колебаний.

Упругие волны

Уравнение волны. Упругой волной называется процесс распространения возмущения в упругой среде. При этом сами частицы среды испытывают только колебания около своих положений равновесия. Если колебания частиц происходят вдоль направления распространения, то волна называется продольной, а если перпендикулярно – поперечной.

Рассмотрим для простоты распространение возмущения вдоль длинного натянутого шнура, который совместим с осью х. В качестве возмущения рассмотрим  - смещение элементов шнура из положения равновесия как функцию координаты и времени =f(x,t). Пусть возмущение распространяется в положительном направлении оси х со скоростью =. Тогда в точку с координатой х возмущение придет с опозданием на время . Итого в момент t в точке х возмущение будет равно

(x,t)=f(t-x/) .

Если волна распространяется в отрицательном направлении оси х, то в скобках будет плюс. Выражение в рамочке – это уравнение волны в общем виде. В частности, уравнение плоской гармонической волны имеет вид

(x,t)=аcos(t-x/)= аcos(t-x/). (23)

а – амплитуда волны,  - циклическая частота колебаний частиц среды. Функция (23) периодична с периодом 2 и по времени и по координате! Поэтому период равен

. (24)

Длиной волны  называется расстояние, проходимое за один период колебаний

=T=,   (25)

Введем волновое число k ==. Тогда уравнение плоской гармонической волны примет симметричный вид

(x,t)=аcos(t-kx). (26)

Легко показать, что  - это фазовая скорость (т.е. скорость распространения вдоль ох некоторой зафиксированной фазы). Действительно, зафиксируем фазу в (23): пусть t-x/=const.  , что и требовалось доказать.

Если волна распространяется в поглощающей среде, то ее амплитуда а будет уменьшаться экспоненциально (из опыта), тогда уравнение волны будет иметь вид

(27)

В плоской волне волновые поверхности (т.е. геометрическое место точек, колеблющихся в одинаковой фазе) имеют вид плоскостей, (в нашем случае плоскости  оси х). Если волновые поверхности - сферы, то волна называется сферической. Фронтом волны называется волновая поверхность, отделяющая область волнового процесса от невозмущенной части среды.

Волновое уравнение. Пусть дано уравнение волны (x,t)=f(t-x/), обозначим фазу φ=(t-x/) и вычислим частные производные по времени и по координате:

; , 

;  (28)

;  (29)

Сравнивая (28) и (29), получим

(30)

Дифференциальное уравнение (30) является одномерным волновым уравнением, в котором  - фазовая скорость. Таким образом,

NB! в стандартной записи волнового уравнения коэффициент при второй производной по времени – величина обратная квадрату скорости распространения волны.

Упругая волна в тонком стержне. Это простейший пример распространения волн в упругой среде. При малых продольных деформациях имеет место закон Гука: , где  - напряжение (Н/м²), относительная деформация, Е – модуль Юнга (Па). Рассмотрим элемент стержня х в момент, когда он оказался в растянутом состоянии. По второму закону Ньютона для этого элемента

xS=F(x+x)+F(x), (31)

где  - плотность, S – площадь поперечного сечения стержня. Справа стоит алгебраическая сумма сил, действующих на выделенный элемент. Так как элемент находится в растянутом состоянии, то F(x+x) >0, F(x)<0, поэтому

F(x+x)+F(x)= S(x+x) - S(x)=, (32)

где учтено, что сила и напряжение слева от х имеют разные знаки (см. рис.11)! Это связано с тем, что в законе Гука  и  должны иметь знаки одинаковые, а у нас – растяжение,   >0,   >0! Подставим (32) в (31) и сократим на Sx; подставим из закона Гука и получим

, (33)

т.е. волновое уравнение,  коэффициент при позволяет выразить фазовую скорость упругой продольной волны:

(34)

В упругой среде можно возбудить и поперечные волны, тогда скорость будет выражаться через модуль сдвига G среды

.

У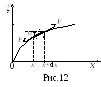пругая волна в гибком шнуре. Рассмотрим малые поперечные колебания шнура. Пусть на малый элемент шнура (рис.12) слева и справа действуют силы F_л и F_пр. Вертикальные проекции этих сил равны: слева; справа , т.к. при малых поперечных колебаниях угол α мал. Алгебраическая сумма этих сил ≈ дифференциалу выражения , т.е. ≈. Введем линейную плотность шнура (масса единицы длины) , тогда второй закон Ньютона для выделенного элемента струны будет иметь вид dx=F dx, или

. (35)

Это вновь волновое уравнение, где множитель при второй производной от смещения по времени определяет фазовую скорость волны

(36)

Упругая волна в жидкостях и газах . Вывод волнового уравнения (33), полученного для тонкого стержня, можно повторить для жидкости или газа, выделив мысленно в этих средах тонкий цилиндрический канал в направлении распространения плоской волны. Необходимо только выяснить, что в этом случае играет роль модуля Юнга. При продольных волнах в среде в них возникают сжатия и разряжения отдельных слоев и закон Гука выражает связь избыточного давления с относительным изменением длины выделенного элемента . Причем, если р>0, давление на выделенный элемент увеличивается,  он сжимается,   <0, т.е. приращения давления р и длины  противоположны по знаку:

.

Умножив числитель и знаменатель в правой части на площадь поперечного сечения канала, получим

,  ,  . (37)

Поскольку масса выделенного элемента не меняется,  V=const, (- плотность)  dV+dV=0, или d/ =- dV/V. Тогда , что после подстановки в (34) позволяет получить выражение для скорости продольных волн в жидкой или газовой среде

. (38)

В частности, в газе процесс распространения звуковых волн (упругие продольные волны в звуковом диапазоне частот) можно считать адиабатическим: pV^=const. Дифференциал логарифма этого выражения равен нулю: ,   (37),  ,  скорость звуковой волны в газе равна , что с учетом уравнения Менделеева-Клапейрона можно

преобразовать к виду . Последняя формула является менее общей по сравнению с (38), однако очень удобна для оценки скорости звука в различных газах. (Кто-то еще помнит, что и называется показателем адиабаты? Не побоюсь спросить: а что такое i ?)

Энергия упругой волны. К закрепленной с одного конца струне (стержню) приложим с другой стороны растягивающую силу, которая по закону Гука в пределах упругой деформации должна изменяться пропорционально смещению: F=x, где  - коэффициент упругости. Для нахождения работы этой силы необходимо проинтегрировать выражение Fdx=xdx в пределах от 0 до х. Поэтому работа равна А=. Эта работа идет на увеличение упругой энергии стержня,  потенциальная энергия растянутого на х стержня (струны) равна

U= . (40)

NB! Потенциальная энергия растянутого (сжатого) стержня- это энергия упругой деформации!

Так как в законе Гука ( ) в данном случае =; =,  , 

.

Поскольку Sl – объем стержня длины l, то плотность потенциальной энергии (энергия единицы объема) равна

. (41)

При прохождении продольной волны каждая единица его объема обладает еще и кинетической энергией, плотность которой, очевидно, равна половине произведения плотности на квадрат скорости удлинения, поэтому плотность полной энергии равна сумме

. (42)

Выразим модуль Юнга через скорость из (34)(42), тогда

. (43)

Продифференцировав уравнение волны (23) по времени и по координате, легко (?!) убедиться, что оба слагаемых равны друг другу, 

NB! Плотности кинетической и упругой (потенциальной) энергии в этой волне одинаковы и изменяются синхфазно!

В частности, плотность энергии волны можно выразить как . Тогда для гармонической волны (x,t)=аcos(t-kx) плотность энергии равна

w=а²² sin² (t-kx) . (44)

Среднее значение плотности энергии за период (или за t>>T) равно

(45)

поскольку среднее значение квадрата синуса за период равно ½. Полученное выражение справедливо также и для упругих волн в жидкостях и газах.

Плотность потока энергии. Вектор Умова. Потоком энергии Ф называется количество энергии переносимое волной через поверхность S в единицу времени . Поток энергии в разных точках поверхности S может быть разным. Чтобы более детально охарактеризовать это обстоятельство вводят понятие плотности потока энергии: это поток энергии через единичную площадку, перпендикулярную к направлению переноса энергии: . Если φ – угол между нормалью к dS и направлением переноса энергии (совпадающим с), то

энергию dW(=wdV), переносимую через dS за время dt можно выразить через скорость и w:

dW= w dt dScosφ, , . И поскольку направление совпадает с направлением переноса энергии, то аналогично можно записать и вектор плотности потока энергии (вектор Умова):

. (46)

Из выражения (46) видно, что величина вектора плотности потока энергии пропорциональна w, среднее по времени значение которой определяется формулой (45), поэтому и среднее значение вектора

. (47)

Интенсивность волны – это I=, т.е. модуль среднего по времени вектора плотности потока энергии –средний модуль вектора Умова.

NB! Интенсивность пропорциональна квадрату амплитуды и квадрату частоты волны.

Связь между вектором и полным потоком Ф через произвольную поверхность S очевидна

. (48)

Стоячие волны. Опыт показывает, что при одновременном прохождении в среде нескольких волн колебания частиц среды оказываются векторной суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. В этом состоит принцип суперпозиции (наложения) волн. Рассмотрим практически важный случай, когда две гармонические волны ₁ и ₂ с одинаковыми частотами и амплитудами распространяются в противоположных направлениях оси х:

; ;

где для простоты начальные фазы выбраны равными нулю. Суперпозиция этих волн дает

, (49)

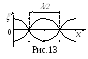-это и есть уравнение стоячей волны. Если рассматривать |2аcoskx| как амплитуду, то выражение (49) представляет собой колебание с частотой  и амплитудой, зависящей от координаты (рис.13). Такое явление называется стоячая волна (в отличие от ранее рассмотренных – бегущих волн). В точках, где 1 находятся максимумы, которые для стоячей волны называются пучностями; а при =0 – узлы. Период функции , поэтому интервал между соседними узлами или пучностями равен половине длины волны /2. Между двумя соседними узлами все точки колеблются синхфазно, но при переходе через узел фаза меняется на , поэтому колебания по разные стороны от узла происходят в противофазе. Таким образом, узлы делят среду на независимые области длиной /2, в которых происходят независимые и никуда не распространяющиеся колебания. Никакой передачи энергии через узлы не происходит, нет распространения возмущения вдоль оси х. Стоячие волны в большей степени являются колебаниями, чем собственно волнами.

Продифференцировав (49) по времени, найдем скорость частиц среды , а продифференцировав по координате – относительную деформацию :

; . (50)

Следовательно, скорость и деформация тоже являются стоячими волнами, сдвинутыми относительно друг друга по фазе на как в пространстве, так и во времени. Поскольку кинетическая энергия ведет себя как квадрат скорости, а потенциальная – как квадрат смещения, то соответственно происходят и превращения энергии стоячей волны: то полностью в потенциальную (упругую), то полностью в кинетическую. При этом в момент максимального смещения наиболее растянуты области узлов,  там запасена потенциальная энергия; в момент нулевого смещения максимальная скорость в пучностях,  там максимальна кинетическая энергия. Таким образом, внутри области размером /2 происходят превращения потенциальной энергии в кинетическую и наоборот, соответственно передача энергии от узлов к пучностям и наоборот. При этом никакого переноса энергии через узлы и ее распространения не происходит. Величина среднего потока энергии через любую плоскость, перпендикулярную оси х равна нулю.

Колебания струны, закрепленной с обоих концов. При возбуждении в струне поперечного возмущения, в ней могут возникнуть стоячие волны, но не любой частоты. Это связано с очевидными граничными условиями: на концах струны должны быть узлы. Отсюда следует, что на струне длиной l должно укладываться целое число полуволн:. Это значит, что могут быть возбуждены колебания с длинами волн, подчиняющимися условию , или частот , где n=1,2,3…; а фазовая скорость (см. 36) зависит от силы, приложенной к струне (сила натяжения), и линейной плотности материала струны.

Частоты, определяемые по формуле

(51)

называются собственными частотами струны; частоту ₁ (n=1) называют основной частотой, остальные частоты (n=2,3,…) – обертонами. Гармонические колебания с частотами (51) называются собственными колебаниями, или гармониками.

Звуковые волны. Так называется распространяющийся в упругой среде волновой процесс (в диапазоне от 20 Гц до 20 кГц), воспринимаемый человеческим ухом. Упругие волны с частотой меньше 20 Гц называются инфразвуком, больше 20 кГц – ультразвуком. Звук различают по высоте, тембру и громкости. Высота звука определяется его частотой: чем больше , тем выше звук. Тембр звука определяется всем набором частот этого звука, который называется его акустическим спектром. Этот спектр может состоять из непрерывного или дискретного набора частот. Именно тембром определяются отличия в звучании музыкальных инструментов.

Громкость звука – это мера слухового ощущения, качественно характеризуемая терминами от тихого до громкого. При неизменной частоте громкость звука растет с увеличением его интенсивности I (Вт/м²). Минимальная величина I10^-12 Вт/м² (порог слышимости). При интенсивности звука I10 Вт/м² (порог болевого ощущения) восприятие звука сменяется ощущением давления и боли. Оба порога зависят от частоты колебаний. Субъективное восприятие громкости возрастает значительно медленнее роста интенсивности звука, поэтому используют логарифмическую шкалу, в которой громкость звука оценивают величиной L:

, где L_Б – уровень интенсивности звука в белах (Б), I₀  10^-12 Вт/м² – порог слышимости при частоте 1 кГц. Таким образом, уровень порога слышимости L_Б=0. Обычно пользуются не белами, а в 10 раз меньшей единицей – децибелом:

. (52)

В этих же единицах можно измерять уменьшение (затухание) интенсивности звука на расстоянии. Например, затухание в 20 дБ соответствует уменьшению интенсивности в 100 раз. Действительно: , где - интенсивность в точке, расположенной ближе к источнику.

Эффект Доплера для звуковых волн. Если источник звука, или приемник, или они оба движутся относительно среды, то частота , воспринимаемая приемником отличается от частоты, испускаемой источником . Это явление называется эффектом Доплера, и объясняется уплотнением (разряжением) импульсов, обусловленным движением источника и приемника. Опуская вывод, приведем формулу, связывающую частоты источника  и приемника  :

, (53)

где и - проекции скоростей источника и приемника на ось х, направленную от источника к приемнику,  - скорость звуковых волн в данной среде.