
Елементи аналітичної геометрії в n-вимірному просторі
§ 1. Гіперплощина й півиростір
З
курсу аналітичної геометрії відомо, що
будь-яке рівняння першого степеня
А1х1+
А2
х 2
=
С зображає
на площині х1Ох2
пряму,
перпендикулярну до вектора
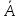 (А1,
А2).
Вектор
(А1,
А2).
Вектор
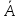 (А1,А2)
називають
нормальним
вектором прямої.
(А1,А2)
називають
нормальним
вектором прямої.
Якщо
записати рівняння А1х1
+
А2х2=
С
у
вигляді
рівняння у відрізках на осях, тобто
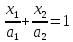 , то
числа а1
а2
виражають
величини відрізків, які пряма відгинає
на координатних осях.
, то
числа а1
а2
виражають
величини відрізків, які пряма відгинає
на координатних осях.
Аналогічно
рівняння А1х1
+
А2х2
+
Аіхі
=
С
у
тривимірному
просторі зображає площину, перпендикулярну
до вектора
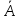 (А1
А2
А3),
який
називають нормальним
вектором площини.
(А1
А2
А3),
який
називають нормальним
вектором площини.
Рівняння
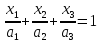 є
рівнянням площини у відрізках
на
осях, числа а1,
а2,
а3
—
величини
відрізків, що відгинаються площиною
на координатних осях.
є
рівнянням площини у відрізках
на
осях, числа а1,
а2,
а3
—
величини
відрізків, що відгинаються площиною
на координатних осях.
Рівняння
площини в тривимірному просторі, а
також прямої на площині, можна подати
у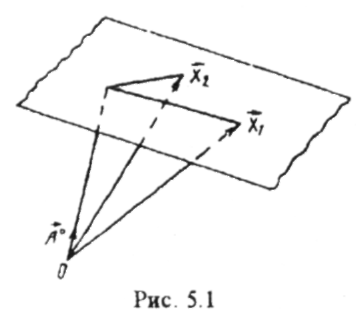
векторній
формі (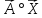 )
=
р,
де
)
=
р,
де
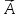 ° —
одиничний
вектор, перпендикулярний до площини,
або
° —
одиничний
вектор, перпендикулярний до площини,
або
нормальний
вектор площини;
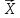 —
поточний
радіус-вектор площини, тобто вектор,
який сполучає початок координат з
довільною
точкою площини;
—
поточний
радіус-вектор площини, тобто вектор,
який сполучає початок координат з
довільною
точкою площини;
р — відстань від початку координат до площини.
Рівняння
(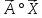 )
=р
означає,
що проекція будь-якого радіуса-вектора
)
=р
означає,
що проекція будь-якого радіуса-вектора
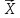 площини на напрям нормального вектора
площини на напрям нормального вектора
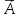 °
дорівнює
р
(рис.
5.1).
°
дорівнює
р
(рис.
5.1).
Узагальненням поняття прямої на площині та площини в тривимірному просторі є поняття гіперплоищни.
!Означення
Гіперплощиною в я-вимірному просторі називають геометричне місце точок (х1,х2,….,хп), координати яких задовольняють рівняння
А1х1 + А2х2 + ... +Апхп= С. (5.1)
Вважатимемо,
що ця гіперплощина нормальна до вектора
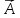 (
A1,
А2,…..,Ап)
і
що рівнянню
(
A1,
А2,…..,Ап)
і
що рівнянню
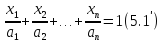
відповідає гіперплощина, яка відтинає на координатних осях відрізки а1 а2, аn.
Векторне
рівняння
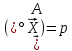 в
n-вимірному
просторі
визначає
гіперплощину, нормальну до одиничного
вектора
в
n-вимірному
просторі
визначає
гіперплощину, нормальну до одиничного
вектора
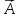 °
і
розміщену на відстані р
від
початку координат. Пряма на площині
ділить її на дві частини, які називають
півплощинами.
Площина
в тривимірному просторі також ділить
весь простір на дві частини, які
називаються півпросторами.
Аналогічно
гіперплощина в n-вимірному
просторі ділить цей простір на дві
частини, кожну з яких називають
півпростором.
°
і
розміщену на відстані р
від
початку координат. Пряма на площині
ділить її на дві частини, які називають
півплощинами.
Площина
в тривимірному просторі також ділить
весь простір на дві частини, які
називаються півпросторами.
Аналогічно
гіперплощина в n-вимірному
просторі ділить цей простір на дві
частини, кожну з яких називають
півпростором.
Нехай
деяка гіперплощина в л-вимірному просторі
задається рівнянням
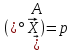 .Тоді
для точок М
одного
з иівиросторів проекції ОС1
векторів,
що їх зображають, на
.Тоді
для точок М
одного
з иівиросторів проекції ОС1
векторів,
що їх зображають, на
напрям
нормального вектора
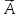 °
менші від р,
а
для точок N
другого
півиростору проекції ОС2
векторів,
що їм відповідають, на
°
менші від р,
а
для точок N
другого
півиростору проекції ОС2
векторів,
що їм відповідають, на
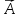 °
більші від р
(рис.
5.2).
°
більші від р
(рис.
5.2).
Отже,
одним з півпросторів є множина векторів
(точок)
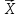 для
яких виконується нерівність
для
яких виконується нерівність
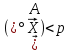 ,
а
для векторів (точок) другого півпростору
—
,
а
для векторів (точок) другого півпростору
—
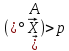 .
Сама
гіпершю шина може бути приєднана до
одного з півпросторів. Тоді вся множина
векторів (точок) n-вимірного
простору поділяється на два види:
вектори (точки), для яких
.
Сама
гіпершю шина може бути приєднана до
одного з півпросторів. Тоді вся множина
векторів (точок) n-вимірного
простору поділяється на два види:
вектори (точки), для яких
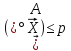 ,
і
точки, для яких
,
і
точки, для яких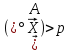 або
навпаки
або
навпаки
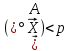 і
і
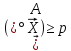 .
Для
того щоб визначити належність
вектора
.
Для
того щоб визначити належність
вектора
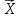 (точки)
до того чи іншого півпростору, треба
координати вектора підставити в
нерівність, що зображає цей півпростір.
Якщо нерівність виконується, то вектор
(точка) належиіь йому, в противному разі
—
не
належить.
(точки)
до того чи іншого півпростору, треба
координати вектора підставити в
нерівність, що зображає цей півпростір.
Якщо нерівність виконується, то вектор
(точка) належиіь йому, в противному разі
—
не
належить.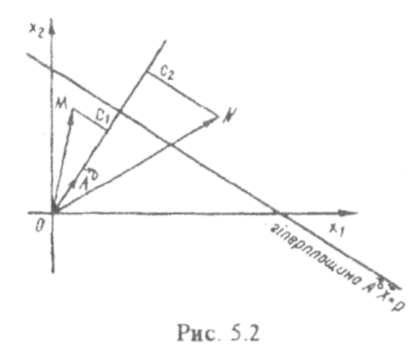
Приклад. Чи належить точха ссмивимірного простору X* (1,0,2,3, 5,-2 4) півпростору 2х1-Зх2-6х3+х4 + x5 -11х6 + 3x7≥4?
Розв'язання. Підставивши координати точки в нерівність, дістанемо 2*1-3*0-6*2+1*3 + 1*5-11*(- 2) + 3*4 = 32 >4
Отже, точка належить заданому півпростору
