
- •Динамика машинного агрегата
- •Структурный анализ рычажного механизма
- •Определение размеров и параметров рычажного механизма
- •3.3. Определение кинематических характеристик механизма.
- •3.3.1. Графическая кинематика механизма.
- •3.3.1.1. Построение планов положений.
- •3.3.2. Аналитическая кинематика механизма.
- •3.4. Определение внешних сил на поршне.
- •3.5. Динамический анализ машинного агрегата.
- •3.5.1. Динамическая модель.
- •3.5.2. Определение приведенного момента инерции.
- •3.5.3. Определение приведенных моментов сил.
3.5.3. Определение приведенных моментов сил.
Mп – условный момент сил на звене приведения элементарная работа или мощности которого равняется сумме элементарных работ или сумме мощности Pi всех внешних сил или моментов сил на звеньях машины.
В курсовом проекте общий момент представляется из двух частей.
![]() ,
,
где
![]() -приведенный
момент движущих сил,
-приведенный
момент движущих сил,
![]() -приведенный
момент сил сопротивления.
-приведенный
момент сил сопротивления.
В
ДВС легкового автомобиля сначала
рассчитывается
![]() ,
например, из равенства мощностей.
,
например, из равенства мощностей.
![]()
![]()
Схема сил на звеньях механизма представлена на рис.3.6.
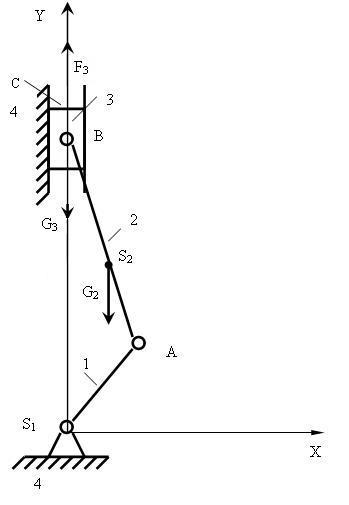
Расчет
![]() производим в соответствии с рис.3.6 из
равенства мощностей по формуле на с.21
в [2]:
производим в соответствии с рис.3.6 из
равенства мощностей по формуле на с.21
в [2]:
![]()
где G2 – сила веса звена 2,
![]()
G3 – сила веса кривошипа 3,
![]()
Для расчетного положения №2:
![]()
Результаты
расчета
![]() для 12 положений приведены в табл.3.6
распечатки первого листа.
для 12 положений приведены в табл.3.6
распечатки первого листа.
3.5.4.
Определение работ Ад,Ас
, приведенного момента инерции
![]() и изменения кинетической энергии
и изменения кинетической энергии
![]() .
.
Т.к.
работа
![]() ,
то рассчитываем сначала работы движущих
сил
,
то рассчитываем сначала работы движущих
сил
![]() по дискретным значениям
по дискретным значениям
![]() численным интегрированием методом
трапеций:
численным интегрированием методом
трапеций:
![]()
![]()
где
![]() - угловой шаг интегрирования,
- угловой шаг интегрирования,
![]()
В
начале цикла
![]() За цикл установившегося движения работа
движущих сил равна работе сил сопротивления
За цикл установившегося движения работа
движущих сил равна работе сил сопротивления
![]() ,
т.е. в курсовом проекте
,
т.е. в курсовом проекте
![]() .
.
Считая
![]() при установившемся движении постоянным,
то получим:
при установившемся движении постоянным,
то получим:
![]() ,
отсюда
,
отсюда
![]()
Работа сил сопротивления в каждом положении:
![]()
Избыточная
работа
![]() равна сумме работ:
равна сумме работ:
![]()
3.5.5.
Определение постоянной составляющей
приведенного момента инерции
![]() и момента инерции маховика
и момента инерции маховика
![]() .
.
Используем
метод Мерцалова Н.П., при котором
рассчитывается значение изменяющейся
кинетической энергии от звеньев с
![]() =const.
=const.
![]() ,
где
,
где
![]() -
кинетическая энергия звеньев с переменным
-
кинетическая энергия звеньев с переменным
![]() .
.
![]() ,
,
![]()
Результаты
расчетов
![]() приведены в табл.3.6 распечатки первого
листа. Из массива значений
приведены в табл.3.6 распечатки первого
листа. Из массива значений
![]() находим наибольшее значение
находим наибольшее значение
![]() и наименьшее
и наименьшее
![]() ,
тогда максимальный перепад кинетической
энергии:
,
тогда максимальный перепад кинетической
энергии:
![]() .
.
Тогда
постоянная часть
![]() ,
которая обеспечит более равномерное
вращение кривошипа с заданным коэффициентом
неравномерности
,
которая обеспечит более равномерное
вращение кривошипа с заданным коэффициентом
неравномерности
![]() при средней скорости установившегося
движения
при средней скорости установившегося
движения
![]() ,
будет равно:
,
будет равно:
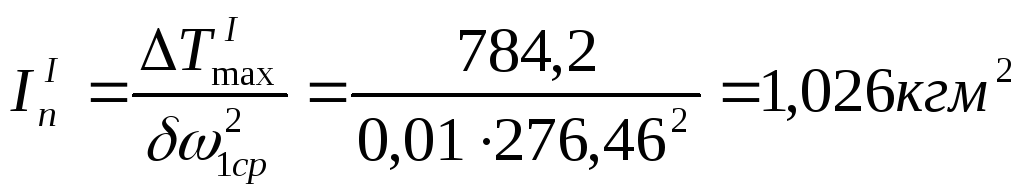 .
.
Момент инерции маховика определяется как :
![]() ,
где
,
где
![]() -
момент инерции всех вращающихся звеньев
машины.
-
момент инерции всех вращающихся звеньев
машины.
Принимая маховик в форме диска, определяем его маховой момент:
![]() .
.
Задаваясь
конструктивно наружным диаметром
![]() ,
определяем массу маховика:
,
определяем массу маховика:
![]()
3.6. Динамический анализ движения звена приведения.
Необходимо
определить действительную угловую
скорость![]() кривошипа 1 и его угловое ускорение
кривошипа 1 и его угловое ускорение
![]() внутри цикла установившегося движения
при найденном параметре
внутри цикла установившегося движения
при найденном параметре
![]() .
.
Скорость
![]() определим из уравнения кинетической
энергии вращающихся звеньев с
определим из уравнения кинетической
энергии вращающихся звеньев с
![]() :
:
![]() ,
откуда
,
откуда
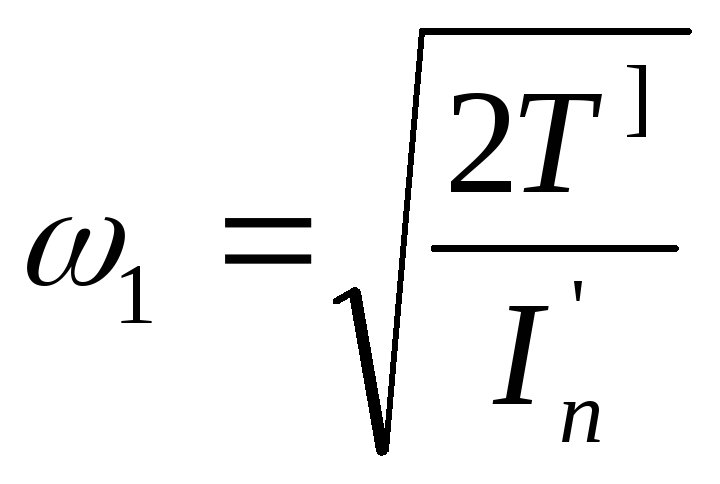 .
.
Кинетическую
энергию T1
определяют по
методу Мерцалова Н.И., используя
зависимость
![]() (см. рис.3.7).
(см. рис.3.7).
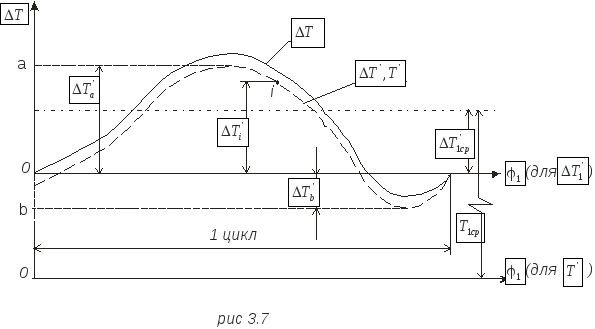
Из
рис.3.7
![]() ,
,
где
![]() -
среднее значение
-
среднее значение
![]() ,
,
![]() -
среднее значение изменения
-
среднее значение изменения
![]() ,
,
![]() ,
,
![]() -
рассчитанные ранее значения
-
рассчитанные ранее значения
![]() в i-ом
положении.
в i-ом
положении.
Угловое ускорение определяется из уравнения движения звена приведения в дифференциальной форме:
![]() ,
откуда
,
откуда
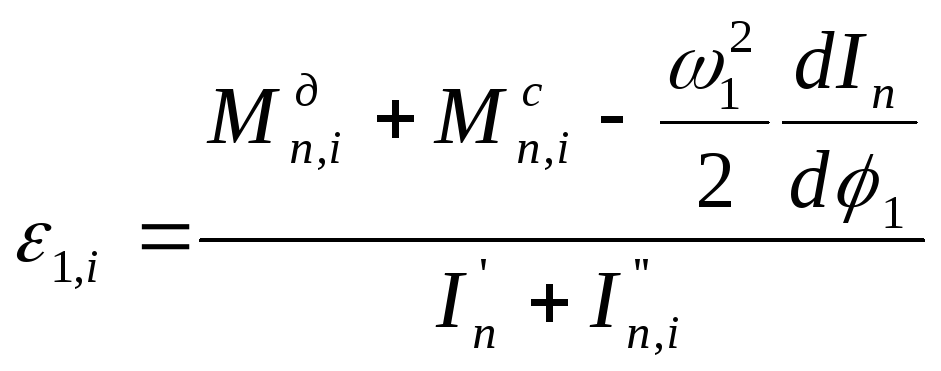 .
.
Результаты
расчетов
![]() и
и
![]() для 12 положений приведены в распечатке
ЭВМ 1 листа (табл.3.6).
для 12 положений приведены в распечатке
ЭВМ 1 листа (табл.3.6).
3.7. Расчет динамики машины на компьютере.
Процесс расчета на ЭВМ включает следующие этапы:
1) Составление математического и логического алгоритма расчета.
2) Составление графического алгоритма программы.
3) Запись программы на алгоритмическом языке.
4) Набор и отладка программы на компьютере.
5) Подготовка исходных данных.
6) Счет на ЭВМ.
3.7.1. Графический алгоритм расчета динамики машины на компьютере.
![]()
![]()
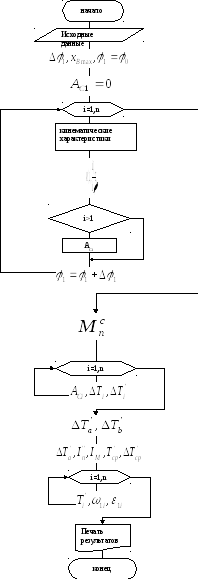
3.8. Обработка результатов вычислений.
По результатам расчетов на компьютере в табл. 3.4-3.6 строим на листе 1:
1) графики кинематических характеристик движения ползуна 3 с т.В (поз.4 листа 1).
а)
график перемещения
![]() т.В ползуна от дальнего крайнего положения
1 в масштабе
т.В ползуна от дальнего крайнего положения
1 в масштабе
![]() с ординатами
с ординатами
![]() (табл.3.4);
(табл.3.4);
б)
график аналога скорости ползуна 3
![]() в масштабе
в масштабе
![]() с ординатами
с ординатами
![]() (табл.3.4).
(табл.3.4).
в)
график аналога ускорения ползуна 3
![]() в масштабе
в масштабе
![]() с ординатами
с ординатами
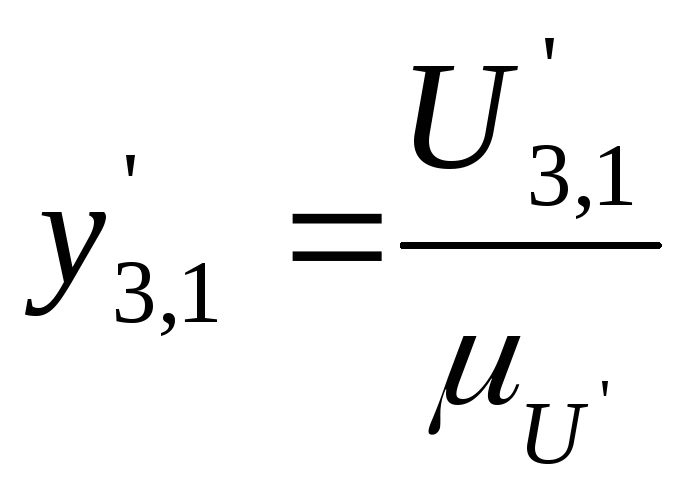 (табл.3.4).
(табл.3.4).
2)
График переменной составляющей
приведенного момента инерции
![]() и его слагаемых
и его слагаемых
![]() ,
,![]() ,
,
![]() в поз.5 листа 1 с масштабным коэффициентом
в поз.5 листа 1 с масштабным коэффициентом
![]() и ординатами
и ординатами
![]() (табл.3.5),
(табл.3.5),
![]() ,
,
![]() ,
,
![]() .
.
3)
Графики приведенных моментов сил
движущих
![]() и сопротивления
и сопротивления
![]() в поз.6 листа 1 с масштабным коэффициентом
в поз.6 листа 1 с масштабным коэффициентом
![]() и ординатами
и ординатами
![]() ,
,
![]() .
.
4)
Графики работ движущих сил
![]() и сил сопротивления
и сил сопротивления
![]() в поз.7 листа 1 с масштабным коэффициентом
в поз.7 листа 1 с масштабным коэффициентом
![]() и ординатами
и ординатами
![]() и
и
![]() .
.
5)
Графики изменения кинетической энергии
всей машины
![]() и от постоянной части
и от постоянной части
![]() в поз.8 листа 1 с масштабным коэффициентом
в поз.8 листа 1 с масштабным коэффициентом
![]() и ординатами
и ординатами
![]() и
и
![]() .
.
6)
Графики угловой скорости кривошипа 1
![]() и углового ускорения
и углового ускорения
![]() за цикл установившегося движения в
поз.9 листа 1 с масштабным коэффициентом
за цикл установившегося движения в
поз.9 листа 1 с масштабным коэффициентом
![]() и
и
![]() и ординатами
и ординатами
![]() ,
,
![]() .
.
3.9. Анализ результатов вычислений и построений.
Для
обеспечения более равномерного вращения
кривошипа с заданным коэффициентом
![]() необходима постоянная часть
необходима постоянная часть
![]() .
Т.к. полученный
.
Т.к. полученный
![]() ,
то необходим маховик с моментом инерции
,
то необходим маховик с моментом инерции
![]() .
.
С
маховиком угловая скорость
![]() внутри цикла изменяется незначительно
между максимальным значением
внутри цикла изменяется незначительно
между максимальным значением
![]() и минимальным
и минимальным
![]() ,
соответственно угловое ускорение
,
соответственно угловое ускорение
![]() и
и
![]() .
.
Выводы:
-
Для обеспечения равномерного вращения кривошипа 1 с заданным коэффициентом
 необходима постоянная часть приведенного
момента инерции
необходима постоянная часть приведенного
момента инерции
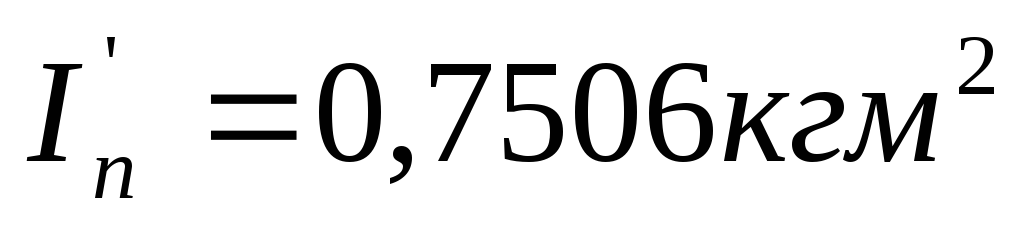 и моментом инерции маховика
и моментом инерции маховика
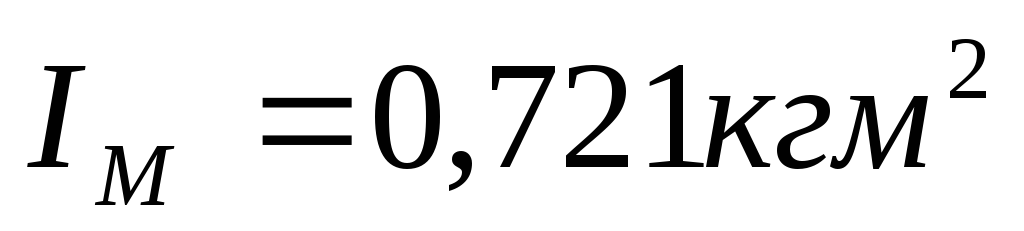 .
. -
Как видно из графиков
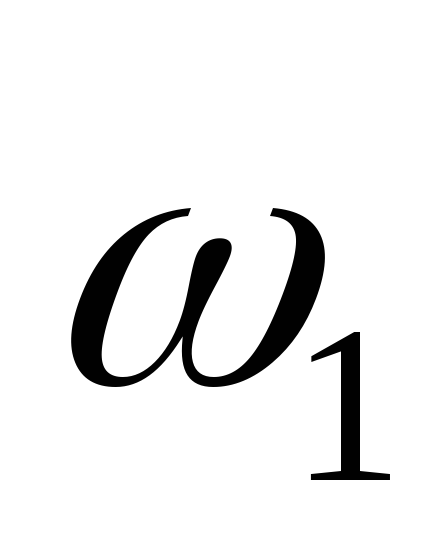 и
и
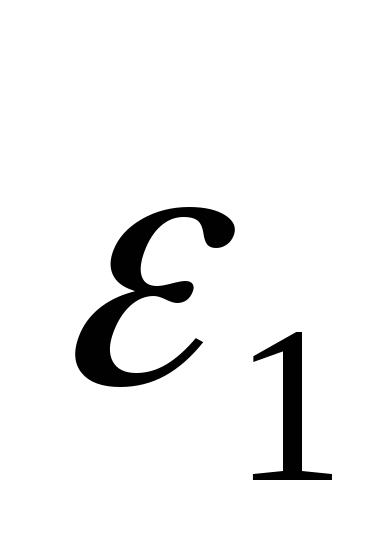 в поз.9 л.1 кривошип вращается неравномерно
с
в поз.9 л.1 кривошип вращается неравномерно
с
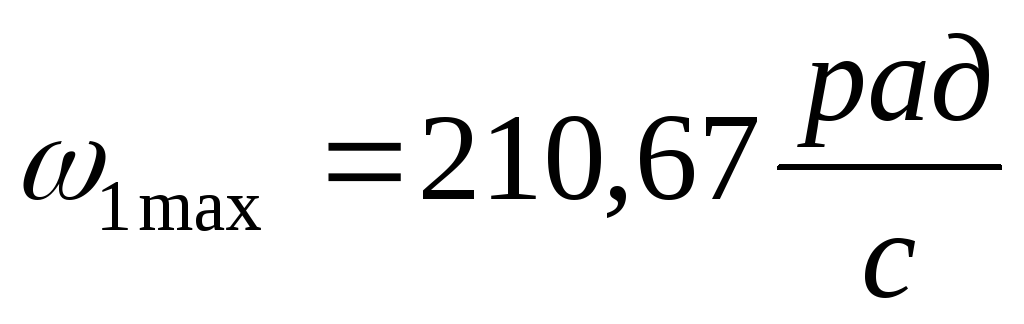 и
и
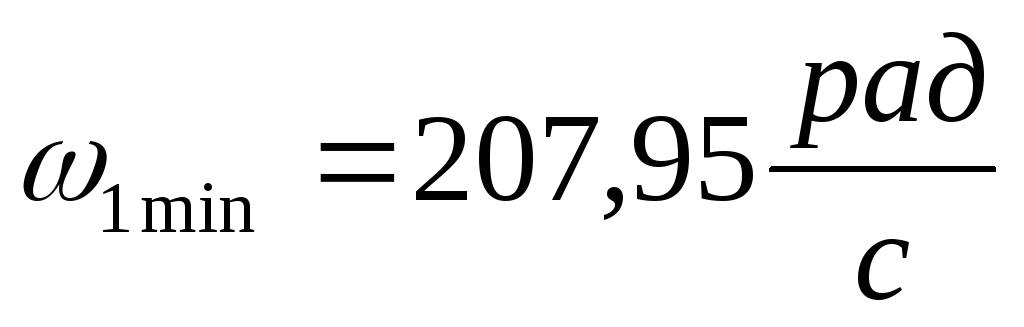 ,
что дает практический коэффициент
неравномерности
,
что дает практический коэффициент
неравномерности
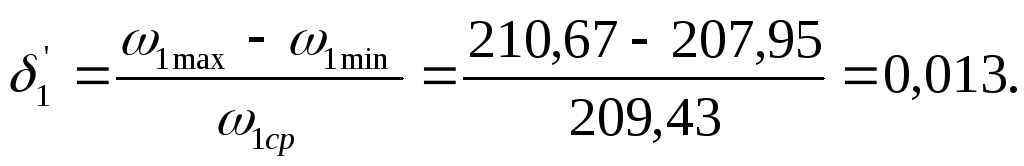
-
Максимальное значение приведенного момента инерции
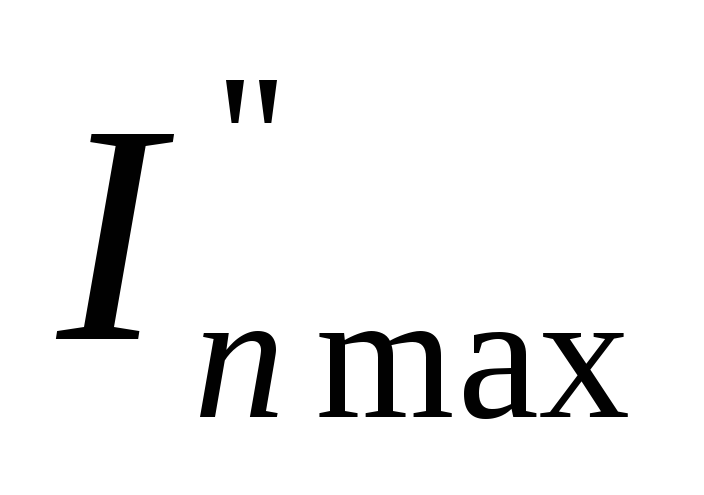 в положение №4
в положение №4
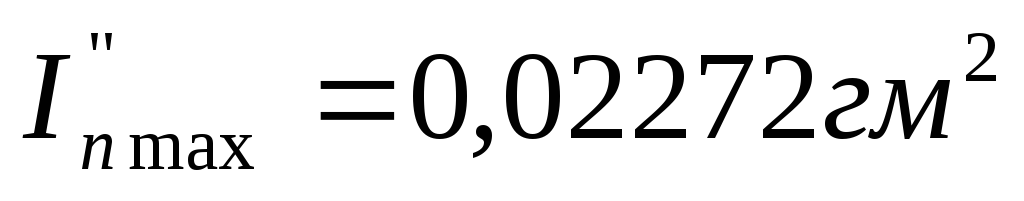 ,
,
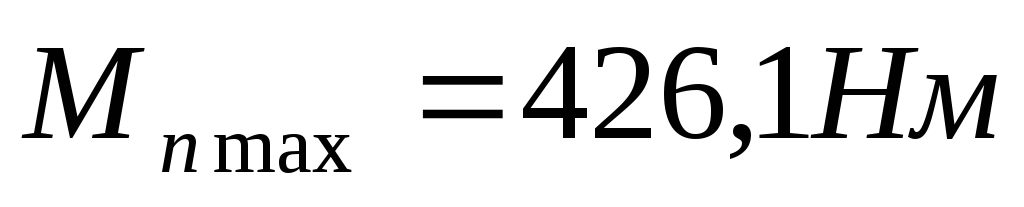 в положении №2
в положении №2 -
Необходима номинальная мощность двигателя
![]() .
.
Коэффициент
динамичности вращения
![]() .
.
Коэффициент
инерционности вращения привода:
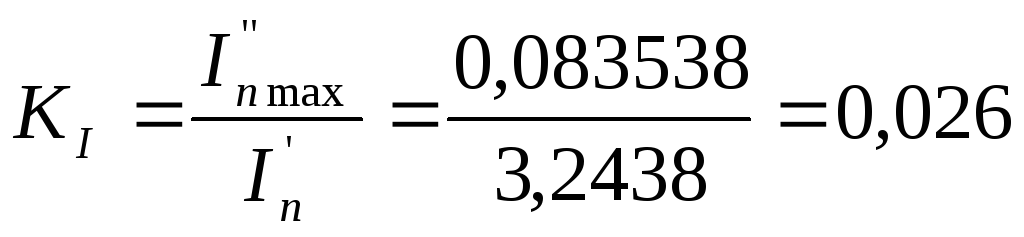 .
.
Малые
значения
![]() ,
КД,
и КI
говорят о
хорошем качестве работы машины.
,
КД,
и КI
говорят о
хорошем качестве работы машины.
![]()
