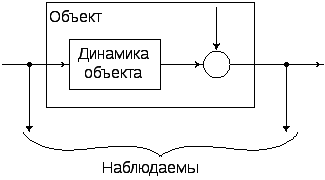
В6. Принципы построения идентификационных схем

Несколько простых примеров возможных идентификационных схем представлено на рис 9, где и - входной и выходной сигналы объекта соответственно; и - входной и выходной шумы.

Проблема идентификации (оценивания) существенно осложняется многосвязностью (многомерностью) объекта: в этом случае входные и выходные сигналы являются векторными переменными и . Другая тонкость связана с тем, что шум может быть не только аддитивным, но и мультикативным.

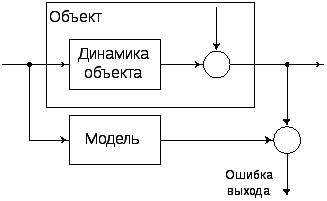
Как уже говорилось, задаче оценивания можно дать следующее математическое описание. На объект и модель действует один и тот же входной сигнал. Сравниваются искаженный помехой выходной сигнал объекта и выходной сигнал модели. Необходимо определить оптимальный в заданном смысле способ корректирования модели. Значения параметров непосредственному наблюдению не доступны. Таким образом, критерием выбора оптимума должен быть функционал от выходных сигналов или от математического ожидания ошибок оценок параметров.

а)	б)
в)
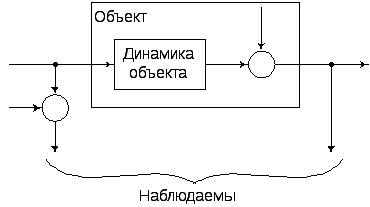
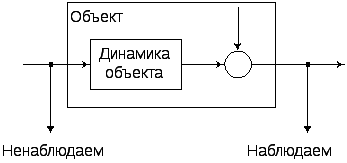
Рис. 9. Примеры идентификационных схем

Часто критерий параметрической идентификации записывается как функционал ошибки, например

,

где - выход объекта; - выход модели; - ошибка; , , - рассматриваются как функции, определённые на интервале . Этот критерий можно интерпретировать как критерий наименьших квадратов для ошибки .

Будем говорить, что рассматривается выходная ошибка, если

,

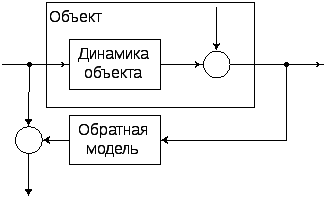
где - выходной сигнал модели, на вход которой подаётся сигнал . Это определение соответствует структуре, изображённой на рис 10, а, где единственной помехой является белый шум измерений выходного сигнала .

Если

,

где - входной сигнал модели; - выходной сигнал модели; тогда говорят, что - входная ошибка (рис. 10 б).

Обозначение предполагает, что модель обратима, то есть для заданного выхода всегда можно найти единственный входной сигнал. С точки зрения теории оценивания использование входной ошибки правомерно тогда, когда помехи представляют собой белый шум на входе системы. В общем случае ошибку можно определить как:

,

где - обратная модель.

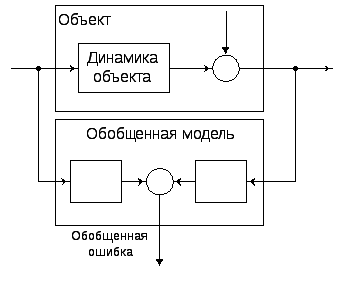
Этот тип модели и ошибки будем называть обобщенными (рис. 10 в).

а)	б)
	Рис. 10
в)

Другой тип задачи идентификации получается при условии, когда решаемая задача является частью семейства вероятностных задач. Такая постановка делает возможным использование теории оценивания и теории принятия решений для нахождения параметров системы. В частности, можно использовать метод максимального правдоподобия, бейесовские методы, минимаксные методы.

Теория оценивания связана со статистической теорией оптимальных систем. Фельдбаум рассмотрел ситуацию, когда управляющее воздействие используется в двух целях:

1. для обучения или изучения характеристик объекта или способов управления объектом;

2. для повышения качества управления, приведения объекта в требуемое состояние.

Такое сочетание изучения и управления Фельдбаум предложил назвать дуальным управлением. Согласно разработанной им теории, в системах дуального управления возникает противоречие между двумя сторонами управляющего воздействия: изучающей и направляющей. Действительно, успешное управление возможно лишь при своевременном воздействии на объект. Однако, успешно управлять можно, лишь достаточно хорошо зная свойства объекта, а для этого необходимо много времени. Преждевременное или запоздалое управление может оказаться неуспешным. Задача оптимизации заключается в наивыгоднейшем сочетании изучения и управления. Принятое решение об определенной в соответствии с заданным критерием величине управления должно учитывать два фактора:

а) потерю, происходящую в значении критерия качества вследствие того, что результат воздействия как в данный момент, так и в последующие вызовет отклонение объекта от требуемого или наилучшего возможного режима; среднюю меру потери называют риском действия;

б) потерю, происходящую в значении критерия качества вследствие того, что значение управляющего воздействия в данный момент оказалось не наилучшим для получения информации о характеристиках объекта, в связи с чем последующие воздействия также оказываются не наилучшими из возможных; среднюю меру такой потери называют риском изучения.