Разноска источника эдс.

Эквивалентное преобразование, представленное на рис.10, носит название разноска источника е. Исходную схему можно заменить на эквивалентную eй схему в соответствии либо с рис.10 б), либо с рис.10 в).

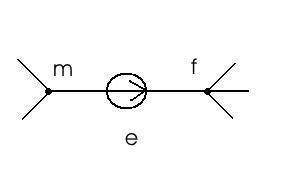
а)

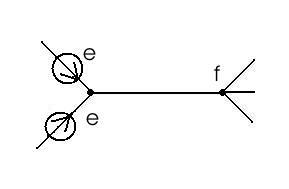
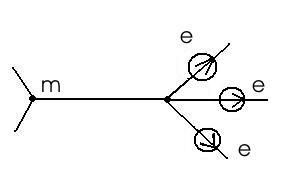
б) в)

Рис.10

а) – исходная схема, б) – разноска источника ЭДС по ветвям, подключенным к узлу m, в) разноска источника ЭДС по ветвям, подключенным к узлу f.

В результате такого преобразования в схеме становится на одну ветвь е меньше. При этом количество узлов также уменьшается на единицу (в исходной схеме два узла m и f, в эквивалентной либо f, либо m).

Задача №1.

Дано: параметры элементов схемы (рис.11), т.е. значения R, е и j;

Найти: токи во всех ветвях и напряжения на источнике тока;

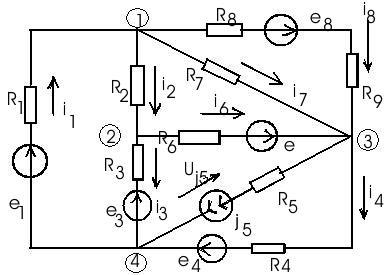
Рис.11

Решение.

Проведем предварительно анализ схемы для выбора рационального метода решения. Схема содержит:

В = 8 – ветвей;

У = 4 узла;

= 1 – ветвей с источниками тока;

= 0 – ветвей е;

По законам Кирхгофа при рациональном выборе совокупности независимых контуров необходимо решить систему из К_ЗК = В – В_i = 7 уравнений. По МКТ – систему из К_МКТ = В – (У-1) – В_i = 4 уравнений. По МУП - К_МУП = У – 1 - В_е = 3. На основание изложенного делаем вывод: наименьший порядок совместно решаемых уравнений, т.е. наиболее рациональный метод, будет при использовании МУП.

Проведем расчет МУП.

1. Схема не содержит ветвей е, поэтому в качестве базового узла можно выбрать любой узел, а так как в схеме 4 узла, то базовому узлу присвоим номер 4, а остальным – номера 1, 2, 3. Потенциал базового узла положим равным нулю .

2. Запишем необходимое количество узловых уравнений

К_МУП = У – 1 - В_е = 3.

Для узла 1 узловое уравнение в общем виде имеет вид:

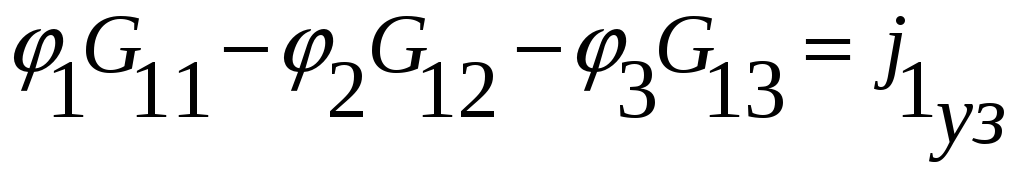1. – это уравнение справедливо для первого узла любой схемы с четырьмя узлами. Для расчетной схемы узловое уравнение

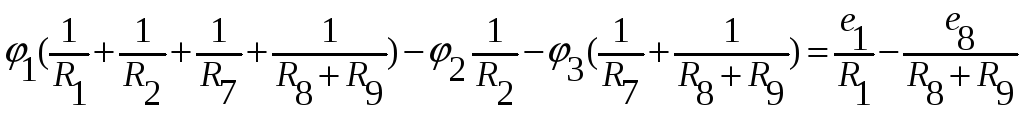, где 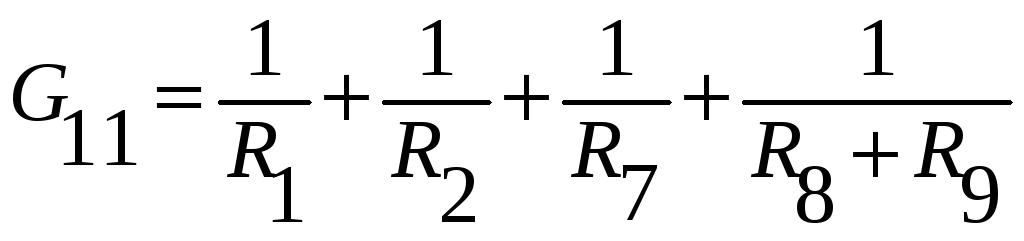– собственная проводимость первого узла содержит 4 слагаемых, т.к. к узлу 1 подходит 4 ветви. В ветви 8 последовательно соединены R₈ и R₉, поэтому ее сопротивление R = R₈ + R₉ и соответственно проводимость 1/R = 1/ R₈ + R₉.

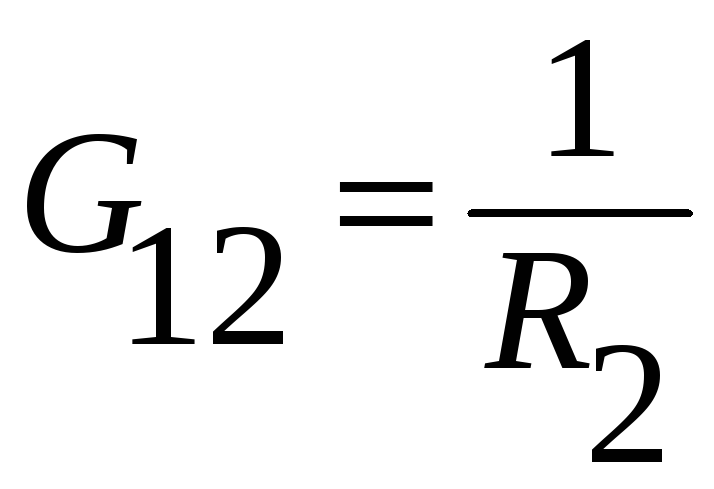– общая проводимость узлов 1 и 2. Между этими узлами включена только ветвь 2.

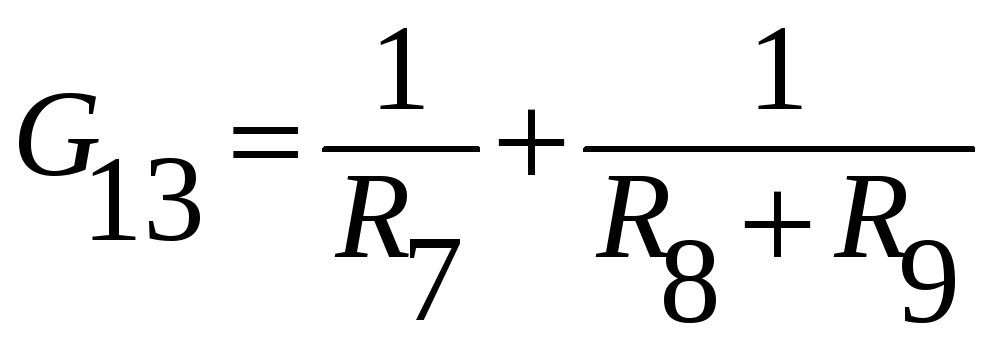– общая проводимость узлов 1 и 3. Имеет два слагаемых, т.к. 1 и 3 узлы соединены двумя ветвями 7 и 8.

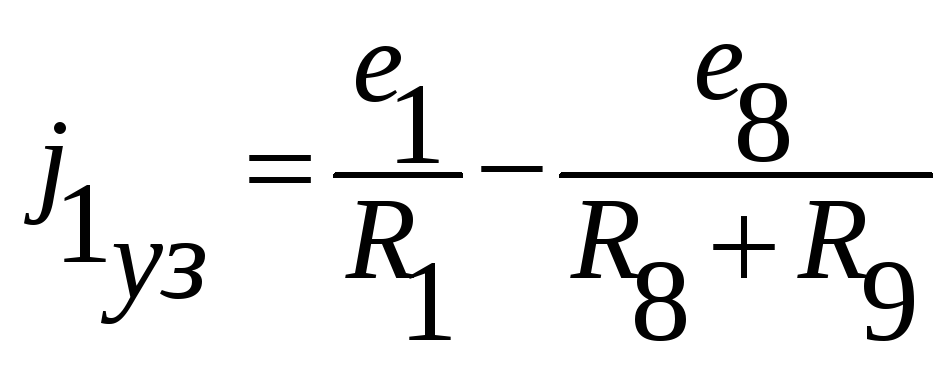– узловой ток узла 1. e₁/ R₁ учитывают со знаком плюс, т.к. е₁ направлено к узлу 1, а е₈/ R₈ + R₉ – со знаком минус, поскольку е₈ направлено от узла 1.

Приведем уравнения для остальных узлов (2 и 3).

2. 

3. 

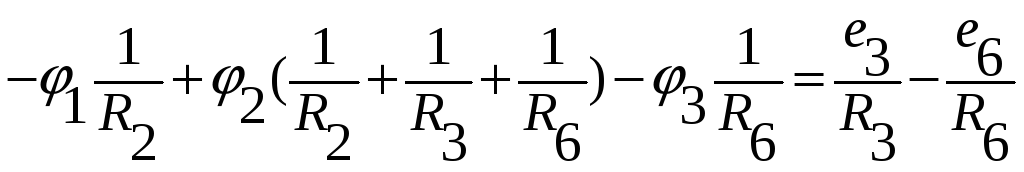
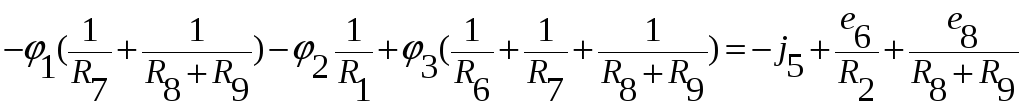
В последнем уравнении отсутствует R₅, т.к. это сопротивление включено последовательно с источником тока (см.замечание 1 п.2). j₅ учитывают в j_3уз со знаком минус, т.к. он направлен от узла 3.

Запишем матрицу коэффициентов левой части уравнений

Матрица проводимостей симметрична относительно элементов главной диагонали, т.е. = . Последнее равенство вытекает из определения общей проводимости между узлами S и m. Это обстоятельство используют для проверки правильности записи узловых уравнений.

Решив систему узловых уравнений, найдем значения потенциалов узлов.

3. Рассчитаем токи ветвей и напряжений на источниках тока, используя ЗКН. Для этого зададим произвольно положительные направления токов в ветвях и напряжений на источниках тока.

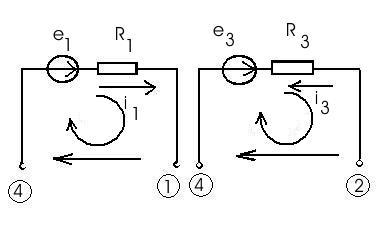
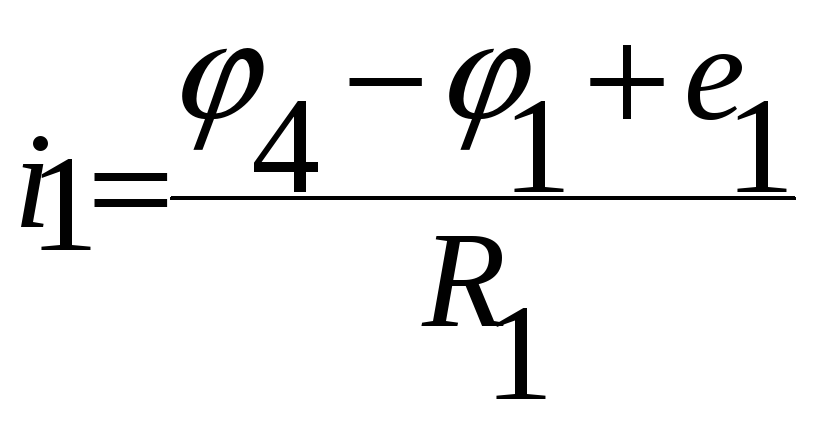
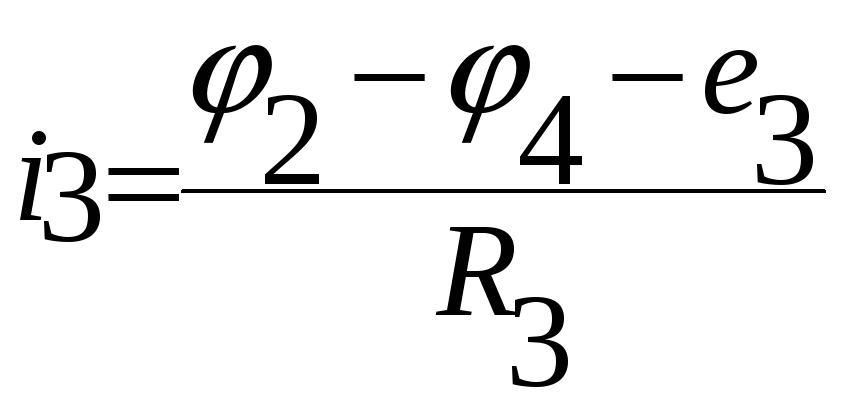
Аналогично для остальных токов.

; ;

;
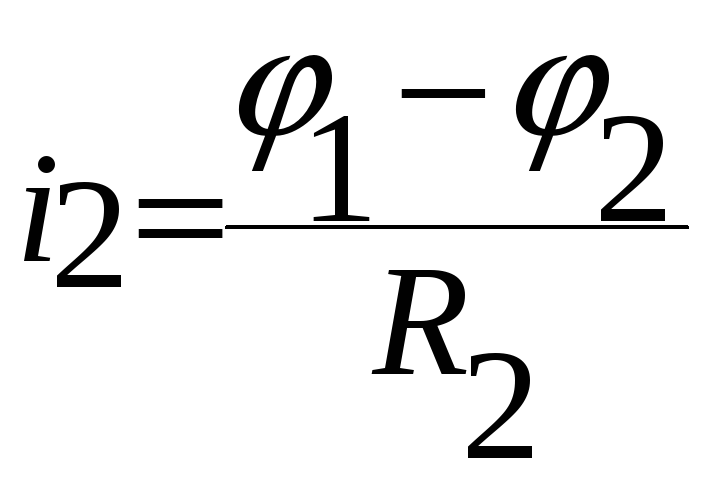
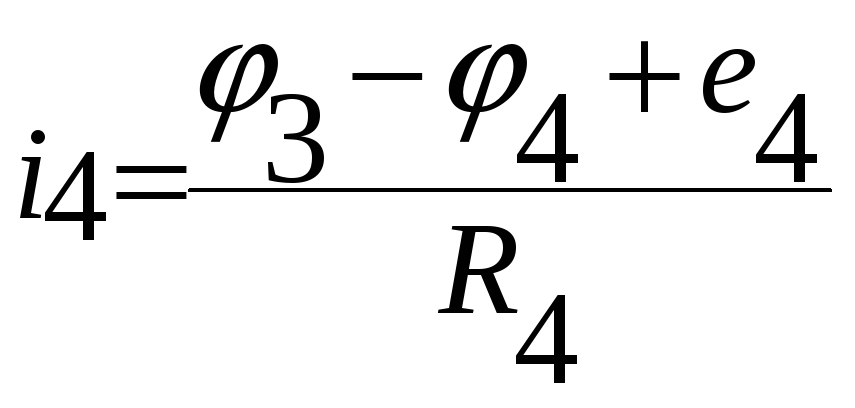
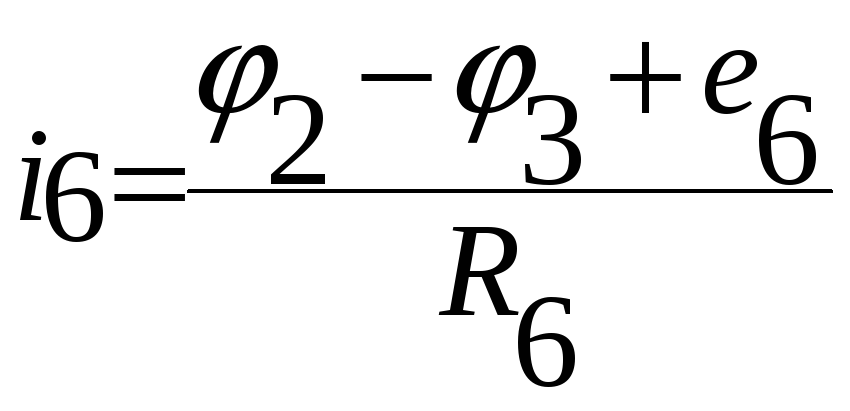
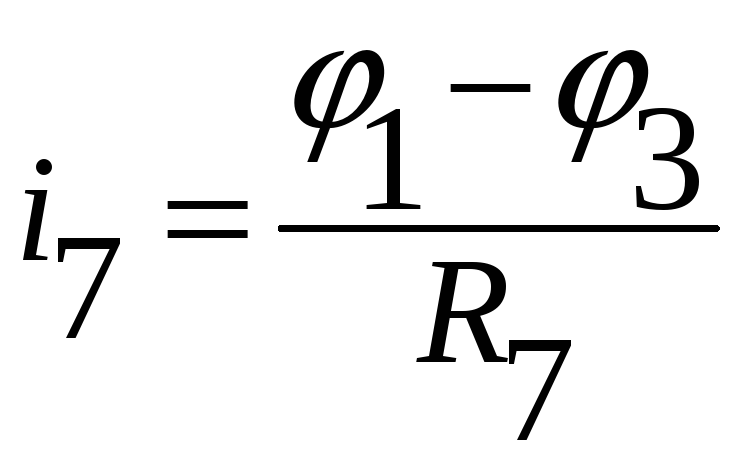
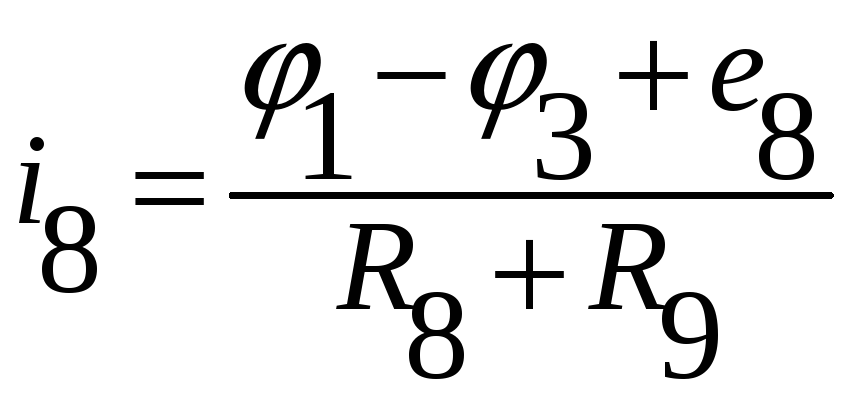