10. Классификация кривых второго порядка.

Доказывается, что для любая кривая 2-го порядка принадлежит к одному из 9 следующих типов кривых:

Эллипс. Каноническое уравнение его: . Точка. Каноническое уравнение ее . Мнимый эллипс. Уравнение его . 4) Гиперболоид. Уравнение ее .

5) Пара пересекающихся прямых. Уравнение ее . Парабола. Уравнение ее . Пара параллельных прямых. Уравнение ее . Пара совпадающих прямых. Уравнение ее . Пара мнимых параллельных прямых. Уравнение ее .

10. Классификация поверхностей второго порядка.

Доказывается, что для любая поверхности 2-го порядка принадлежит к одному из 17 следующих типов поверхностей:

Эллипсоид. Уравнение ее в соответствующей системе координат имеет вид: (см. рис. 2). Точка. Уравнение ее . Мнимый эллипсоид. Уравнение ее . Однополостный гиперболоид. Уравнение ее (см. рис. 9). Двуполостный гиперболоид. (см. рис. 11). Конус. Уравнение в соответствующей системе координат (см. рис. 8). Эллиптический параболоид. (см. рис. 12). Гиперболический параболоид. (см. рис. 13).

Эллиптический цилиндр. Уравнение ее (см. рис. 4). Прямая. Уравнение ее . Мнимый эллиптический цилиндр. Уравнение ее . Гиперболический цилиндр. Уравнение ее (см. рис. 5). Пара пересекающихся плоскостей. Уравнение ее (см. рис. 15). Параболический цилиндр. Уравнение ее (см. рис. 6). 15) Пара параллельных плоскостей. Уравнение ее (см. рис. 16). Пара мнимых параллельных плоскостей. Уравнение ее . Пара совпадающих параллельных плоскостей. Уравнение ее (совпадает с плоскостью Oyz).

11. Приведение кривой второго порядка и поверхности второго порядка к каноническому виду по методу собственных значений

Любой матрице A порядка n соответствует линейный оператор  в пространстве R ⁿ, заданный формулой (x) = Ax. Справедлива теорема.

Теорема 1. Для любой симметрической матрицы A порядка n в пространстве R ⁿ имеется ортонормированный базис, состоящий из собственных векторов матрицы А.

Алгоритм построения ортонормированного базиса.

1. Составить характеристическое уравнение матрицы det(A- E) = 0 и найти все собственные значения матрицы A.

2. Для каждого собственного значения составить систему однородных линейных уравнений (A- E)X = 0 и найдем фундаментальную систему решений и ортогонализуем ее.

3. Объединяем все полученные ортогональные системы и нормируем полученный базис. Получим ортонормированный базис, состоящий из собственных векторов матрицы А.

Пример. Найти ортонормированный базис пространства, состоящий из собственных векторов матрицы .

1. Составить характеристическое уравнение матрицы и найдем все собственные значения матрицы A

.

2. Найдем собственные векторы, решая системы уравнений:

,,,

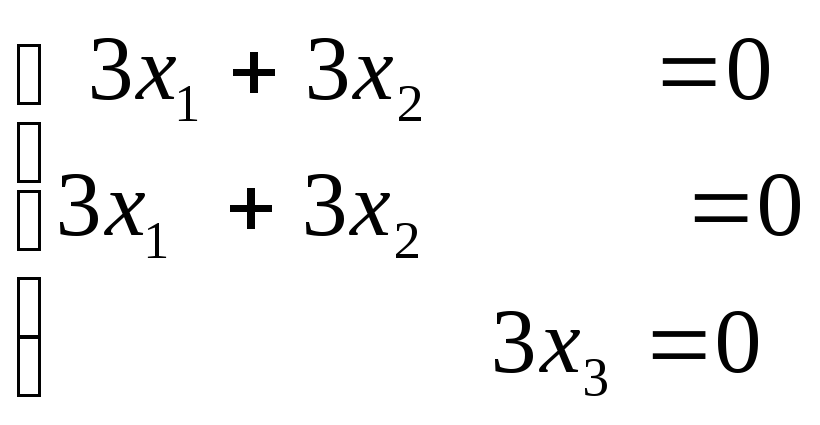Общее решение первой системы (0, 0, x₃ ), фундаментальное решение (0, 0, 1).

Общее решение второй системы (x₂, x₂, 0 ), фундаментальное решение (1, 1, 0).

Общее решение третьей системы (-x₂, x₂, 0 ), фундаментальное решение (-1, 1, 0).

Ортогонализовать в данном случае не нужно, так как каждая фундаментальная система решений состоит из одного вектора.

3. Объединяя и нормируя, полученные векторы получим ортонормированный базис пространства , состоящий из собственных векторов матрицы А: .

Отсюда получаем алгоритм приведения квадратичной формы к каноническому виду:

1. Составить матрицу квадратичной формы.

2. Составить характеристическое уравнение матрицы det(A- E) = 0 и найти все собственные значения ₁, ₂, ..., _n матрицы A.

3. Составить квадратичную форму канонического вида f = (при необходимости методом, указанным выше, можно найти канонический базис, в котором квадратичная форма имеет канонический вид.

Пример. Квадратичная форма f(x₁, x₂, x₃) = в силу предыдущего примера имеет канонический вид

f = канонический базис .

Рассмотрим преобразование общей поверхности  второго порядка, заданной уравнением (1) к частным случаям.

1. Выполним ортогональное преобразование поверхности , при котором квадратичная форма перейдет в квадратичную форму канонического вида , где все собственные значения ₁, ₂, ..., _n матрицы A =(a_ij). При этом поверхность  в новой системе координат Oy₁y₂y₃ будет иметь уравнение

. (22)

2. Если _i  0, то соответствующий линейный член A'_i в уравнении (2) можно исключить, выполнив преобразование по формулам 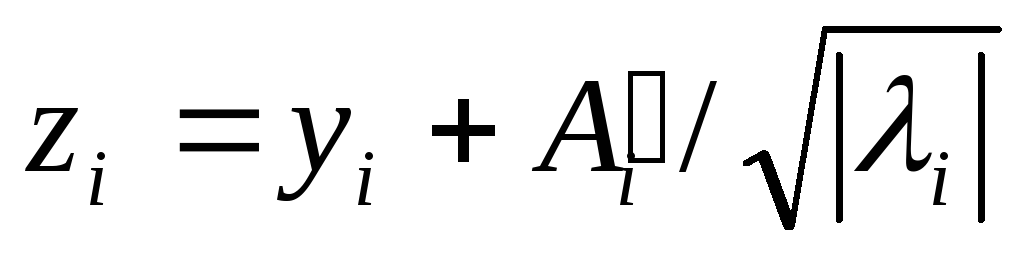, если _i  0, и z_i = y_i, если _i = 0. Уравнение поверхности  примет вид:

. (23)

Теперь возможны случаи.

1) Все A'_i = 0 и B" = 0. Тогда уравнение (23) поверхности  представим в виде: . Это поверхность видов 2, 6, 10, 13, 17.

2) Все A'_i = 0 и B"  0. Тогда уравнение (23) поверхности  представим в виде: . Это поверхность видов 1, 3, 4, 5, 9, 11, 12, 15.

2) В (3) найдется A'_j  0. ви B"  0. Тогда выполнив преобразование (23) по формулам , w_i = y_i, если i j. Уравнение поверхности  примет вид: .

Это поверхность видов 7, 8, 14.

Пример 2. Определим вид поверхности, определяемой уравнением

.

В силу примера в предыдущем параграфе квадратичная форма поверхности имеет канонический вид f = в каноническом базисе . Напишем преобразования координат

.

После этого уравнение поверхности примет вид:

Выделим полный квадрат , и выполним преобразование переменных по формулам: и получим

.

Разделим обе части на 9/8 получим уравнение

двуполостного гиперболоида.

Пример 1. Определим вид кривой , определяемой уравнением .

Рассмотрим квадратичную форму кривой , и приведем ее к каноническому виду. Составим

характеристическое уравнение кривой и найдем собственные значения и собственные векторы.

.

Составим векторные уравнения, для нахождения собственных векторов

.

Тогда квадратичная форма поверхности имеет канонический вид f = в каноническом базисе, . Напишем преобразования координат . После этого уравнение поверхности примет вид: Выделим полный квадрат , и выполним преобразование переменных по формулам:

и получим . Разделим обе части на 17/5 получим уравнение гиперболы.

.