3. Эквивалентные системы векторов и их свойства.

Лемма 1. Пусть S₁ , S₂ - конечные системы векторов. Если вектор с линейная комбинация векторов системы S₁ и каждый вектор системы S₁ линейная комбинация векторов системы S₂ , то вектор с линейная комбинация векторов системы S₂ .

Доказательство. Пусть S₁ = { a₁, a₂, ..., a_m } , S₂ = { b₁, b₂, ..., b_n } . По по условию:

с = a_i , a_i = b_j (i=1, 2,... , m).

Подставляя вторые равенства в первое получим:

с = (b_j) = b_j .

Лемма доказана.

Определение 3. Две конечные системы векторов S₁ и S₂ называются эквивалентными, если каждый вектор системы S₁ линейная комбинация векторов системы S₂ и каждый вектор системы S₂ линейная комбинация векторов системы S₁.

Эквивалентность систем S₁ и S₂ обозначается символом S₁  S₂ .

Теорема 2. Отношение эквивалентности систем векторов рефлексивно, симметрично, транзитивно, т.е. для любых трех систем S₁, S₂ , S₃ выполняются свойства:

1 S₁  S₁;

2 если S₁  S₂ , то S₂  S₁;

3 если S₁  S₂ и S₂  S₃ , то S₁  S₃.

Доказательство. Так как свойства 1 и 2 очевидны, то докажем свойство 3. Пусть S₁ = { a₁, a₂, ..., a_m } , S₂ = { b₁, b₂, ..., b_n } , S₂ = { c₁, c₂, ..., c_p } . По условию и определению эквивлентности систем векторов каждый вектор a_i  S₁ линейная комбинация векторов системы S₂ и каждый вектор системы S₂ линейная комбинация векторов системы S₃ , то по лемме a_i линейная комбинация векторов системы S₃ . Аналогично доказывается, что каждый вектор с_k  S₃ линейная комбинация векторов системы S₁ . Тогда по определению эквивалентности S₁  S₃ Свойство доказано.

Теорема 3. Если конечные системы векторов эквивалентны, то их ранги равны.

Доказательство. Пусть S₁, S₂ две конечные системы векторов, S₁  S₂. Если какая-нибудь из систем S₁ или S₂ нулевая, то и другая нулевая и тогда ранги обеих систем равны нулю. Пусть S₁ и S₂ ненулевые системы и пусть

b₁, b₂, ..., b_r , (4)

c₁, c₂, ..., c_s , (5)

базисы этих систем соответственно. Тогда rangS₁ = r и rangS₂ = s. Докажем, что r = s.

По определению базиса каждый вектор системы S₁ линейная комбинация векторов системы (4). Так как система (4) базис системы S₁ , то каждый вектор системы (4) содержится в S₁ и поэтому есть линейная комбинация векторов системы S₁ . Поэтому (4)  S₁. Аналогично доказывается, что (5)  S₂. Так как S₁  S₂, то по теореме 2 (4)  (5).

Отсюда каждый вектор системы (4) линейная комбинация векторов системы (5), а по определению базиса система (4) линейно независима. Тогда по основной теореме о двух системах векторов r  s. Аналогично доказавается, что s  r. Из этих двух неравенств следует r = s.

Теорема доказана.

4. Ранг матрицы. Метод элементарных преобразований. Рассмотрим матрицу А размерности mn с элементами из поля Р:

.

Строки этой матрицы образуют конечную систему векторов в арифметическом n-мерном пространстве Рⁿ:

a₁ = (a₁₁, a₁₂, ..., a_1n) , a₂ = (a₂₁, a₂₂, ..., a_2n) , ..., a_m = (a_m1, a_m2, ..., a_mn) . (1)

Определение 1. Рангом матрицы или называется ранг ее системы строк, если строки матрицы рассматривать как n-мерные числовые вектора.

Обозначают ранг матрицы А символом rangA.

Ранг матрицы, в силу замечания, сделанного к определению 4.1, есть максимальное число линейно независимых строк матрицы. Отсюда следует что ранг нулевой матрицы равен нулю, так как ранг системы нулевых векторов равен нулю. Ранг матрицы, определенный выше, называют также строковым рангом матрицы.

Столбцы матрицы есть матрицы размерности m1, которые образуют конечную систему векторов в пространстве матриц Р ^m1 . Столбцовым рангом матрицы называется ранг ее системы столбцов. В дальнейшем будет доказано, что строковой и столбцовый ранги матрицы равны.

Теорема 1. Элементарные преобразования строк матрицы и преобразование выбрасывания нулевой строки не изменяют ранг (строковый ранг) матрицы.

Аналогичное утверждение имеет место для столбцов.

Доказательство. Докажем теорему для каждого преобразования отдельно. При перестановке строк матрицы ранг матрицы не меняется так как множества строк исходной и преобразованной матриц равны.

Умножим какую-нибудь строку матрицы на число c  Р, c  0. Можем считать, что умножается первая строка, так как в противном случае строки матрицы можно переставить не изменяя ранг матрицы. Получим матрицу:

,

строки которой обозначим буквами a₁, a₂, ..., a_m . По определению 1

rangA =rang(a₁, a₂, ..., a_m) , rangA =rang(a₁, a₂, ..., a_m).

Так как

a₁ = ca₁ = ca₁ + 0a₂ + ...+ 0a_m , a₁ = a₁ = a₁ + 0a₂ + ...+ 0a_m ,

a₂ = a₂ = 0a₁ + 1a₁ + ...+ 0a_m , a₁ = a₁ = 0a₁ + 1a₁ + ...+ 0a_m ,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a_m = a_m = 0a₁ + 0a₁ + ...+ 1a_m , a_m = a_m = 0a₁ + 0a₁ + ...+ 1a_m ,

то системы векторов a₁, a₂, ..., a_m и a₁, a₂, ..., a_m эквивалентны и по теореме 4.3 rang(a₁, a₂, ..., a_m) = rang(a₁, a₂, ..., a_m). Поэтому rangA = rangA.

Аналогичным образом доказывается, что ранг матрицы не меняется при прибавлении к одной строке матрацы другой, умноженной на любое число c  Р, и не меняется при выбрасывании нулевой строки.

Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида и при этом ранг исходной матрицы будет равен числу строк в поученной матрице ступенчатого вида.

Доказательство. По теореме 2.1.1.1 любую ненулевую матрицу конечным числом элементарных преобразований и преобразований, выбрасывания нулевой строки можно привести к матрице ступенчатого вида:

,

где b_1k  0, b_2l  0, ..., b_rs  0. По теореме 1 rangA = rangB. Покажем, что rangВ = r, а для этого докажем, что строки b₁, b₂, ..., b_r матрицы B линейно независимы. Действительно, если найдутся такие числа ₁, ₂, ..., _r  Р, что выполняется равенство

₁b₁ + ₂b₁ + ...+ _rb_r = 0,

то, переходя от векторного равенства к равенствам соответствующих координат векторов, стоящих в правой и левой частях этого равенства, получаем систему n числовых равенств:

₁0 + ₂0 + ...+ _r0 = 0,

. . . . . . . . . . . . . .

₁b_1k + ₂0 + ...+ _r0 = 0,

. . . . . . . . . . . . . .

₁b_1l + ₂b_2l + ...+ _r0 = 0,

. . . . . . . . . . . . . .

₁b_1s + ₂b_2s + ...+ _rb_rs = 0,

. . . . . . . . . . . . . .

₁b_1n + ₂b_2n + ...+ _rb_rn = 0.

В силу того, что b_1k  0 , b_2l  0 , ..., b_rs  0 отсюда находим, что ₁ = 0 , ₂ = 0 , ..., _r = 0 . Следовательно, система векторов b₁, b₂, ..., b_r линейно независима и rangB =r. Поэтому и rangА =r. Теорема доказана.

Из теоремы 2 вытекает метод вычисления ранга матрицы, называемый методом элементарных преобразований. Для того, чтобы вычислить ранг матрицы мы матрицу элементарными преобразованиями и вычеркиванием нулевых строк приводим к ступенчатому виду. Тогда по теореме 2 ранг матрицы равен числу строк в полученной матрице ступенчатого вида.

Пример 1. Вычислить ранг матрицы

.

Приводим матрицу А элементарными преобразованиями и вычеркиванием нулевых строк к ступенчатому виду

.
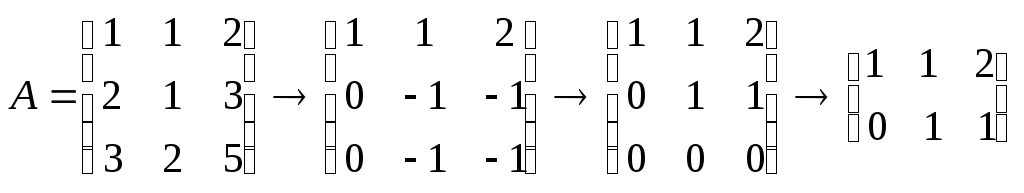