Глава I. Обзор и сравнительный анализ методов и алгоритмов повышения разрешения изображений

1. Анализ исследуемой проблемы

Суть интерполяции заключается в использовании имеющихся данных для получения ожидаемых значений в неизвестных точках.

В первую очередь отметим, что изображение представляется в виде функции f(x, y). Исходя из этого, строится математическая основа интерполяции.

Пиксели изображений являются точками, в которых значение функции известно.

Сутью повышения разрешения изображений, с помощью интерполяции, является нахождение значений функции в промежуточных точках.

Основной недостаток интерполяции – невозможно точно восстановить информацию.

Общепринятые алгоритмы интерполяции можно поделить на две категории: адаптивные и неадаптивные. В данной работе использованы неадаптивные алгоритмы интерполяции.

Адаптивные методы изменяются в зависимости от предмета интерполяции (резкие границы, гладкая текстура), тогда как неадаптивные методы обрабатывают все пиксели одинаково.

Неадаптивные алгоритмы включают:

• метод ближайшего соседа

• билинейный

• бикубический

В зависимости от сложности, они используют от 0 до 256 (или более) смежных пикселей для интерполяции. Чем больше смежных пикселей они включают, тем более точными могут оказаться, но это достигается за счёт значительного прироста времени обработки. Эти алгоритмы могут использоваться как для развёртки, так и для масштабирования изображения. В полной мере работа этих алгоритмов реализована в Photoshop.

К адаптивным алгоритмам можно причислить:

• градиентные методы, основная идея которых использование разных ядер для интерполяции вдоль и поперек границ.

• Обратная задача, постановка задачи в которой производится в виде:

Az=U (1),

где

Z – увеличенное изображение;

U – уменьшенное изображение;

А – оператор, уменьшающий изображение.

Увеличение здесь реализуется как решение этого уравнения с применением итерационных методов. Главный минус этого метода – неустойчивость, т.к. задача поставлена некорректно.

• Регулязирующий метод. Одним из способов решения этой некорректной задачи (1) является метод регуляции, созданный академиком А. И. Тихоновым. В результате этот метод сводит некорректно поставленную задачу – к корректной, за счет использования дополнительных ограничений.

Адаптивные алгоритмы включают в себя многие коммерческие алгоритмы в лицензированных программах, таких как Qimage, PhotoZoom Pro, Genuine Fractals и другие. Многие из них применяют различные версии своих алгоритмов (на основе попиксельного анализа), когда обнаруживают наличие границы — с целью минимизировать неприглядные дефекты интерполяции в местах, где они наиболее видны. Эти алгоритмы в первую очередь разработаны для максимизации бездефектной детальности увеличенных изображений, так что некоторые из них для вращения или изменения перспективы изображения непригодны.

Рассмотрим более подробно работу неадаптивных алгоритмов интерполяции. В моем проекте применены алгоритмы: билинейная и бикубическая. Так как из простейших и доступных методов интерполяции билинейная более проста в реализации и дает приемлемое качество при увеличении разрешения. А бикубический метод он немного сложен в реализации, но дает очень хорошее качество.

Метод ближайшего соседа - это наиболее базовый из всех алгоритмов интерполяции, который требует наименьшего времени обработки, поскольку учитывает только один пиксель — ближайший к точке интерполяции. В результате каждый пиксель просто становится больше.

Билинейная интерполяция рассматривает квадрат 2x2 известных пикселя, окружающих неизвестный. В качестве интерполированного значения используется взвешенное усреднение этих четырёх пикселей. В результате изображения выглядят значительно более гладко, чем результат работы метода ближайшего соседа.

В вычислительной математике билинейная интерполяция – расширение линейной интерполяции для функций в двух переменных, то есть – это линейная интерполяция первого порядка в двумерном случае:

f(x, y)=(1-x)(1-y)f(0, 0)+x(1-y)f(1, 0)+(1-x)yf(0, 1)+xyf(1, 1) (2).

Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом.

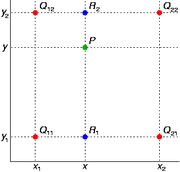
Рис.1. Билинейная интерполяция

Четыре красные точки представляют собой известные значения функции. Значение в зеленой точке должно быть интерполировано.

Допустим, что необходимо интерполировать значение функции f в точке P = (x, y). Для этого необходимо знать значения функций в (окружающих P) точках Q11 = (x1, y1), Q12 = (x1, y2), Q21 = (x2, y1), и Q22 = (x2, y2).

Первым шагом интерполируется (линейно) значение вспомогательных точек R1 и R2 вдоль оси абсцисс, где

R1 = (x,y1)

R2 = (x,y2)

(3)

(4)

Теперь проводится линейная интерполяция между вспомогательными точками R1 и R2.

(5)

Это и есть приблизительное значение функции в точке P, т.е. f(x, y).

(6)

В особом случае, когда известные точки находятся на вершинах единичного квадрата, т.е. имеют координаты (0, 0), (0, 1), (1, 0), и (1, 1), формула билинейной интерполяции упрощается до:

(7).

Или же с помощью умножения векторов с матрицей:

(8).

Обратите внимание: сам интерполянт нелинеен:

(9),

т.к. является произведением двух линейных функций. Альтернативное написание:

(10),

где

. (11).

Результат билинейной интерполяции не зависит от порядка шагов. Возможно сначала интерполировать между известными точками вдоль оси ординат и затем, получив два вспомогательных значения, интерполировать между ними вдоль оси абсцисс. Результат будет тот же.

В компьютерной графике билинейная интерполяция получила широкое распространение в процессе ресэмплинга (или, проще говоря, масштабирования) изображений.

При увеличении цифровых изображений наблюдается сильная пикселизация картинки. Билинейная интерполяция используется для расчета цветов дополнительных пикселей (P) относительно основных, исходных (Q), что позволяет сглаживать переходы. Значением функции f в данном случае выступает цвет пикселя (его составляющие). При этом квадрат, образованный четырьмя рассматриваемыми основными точками принимается единичным.

Главным недостатком билинейной интерполяции при масштабировании изображений является тот факт, что при увеличении в N раз изображения размером W на H пикселей в результате будет получено изображение размером не NW на NH пикселей, а (N(W − 1) + 1) на (N(H − 1) + 1) пикселей.

Связано это с тем, что в исходном изображении, например, по горизонтали имеется W точек, т.е. (W − 1) смежных пар. При увеличении изображения в N раз между каждой парой основных точек вставляется по (N − 1) дополнительных точек (т.е. при увеличении вдвое между основными точками вставляется еще по одной, при увеличении втрое - по две и т.д.). Итого в результате ширина результирующего изображения будет равна сумме количества основных и дополнительных точек:

W + (W − 1)(N − 1) = N(W − 1) + 1 (12).

Проще говоря, для последнего пикселя (в каждой строке и столбце) исходного изображения не находится пары, с которой можно было бы провести интерполирование.

Бикубическая интерполяция

Бикубическая интерполяция идёт на один шаг дальше билинейной, рассматривая массив из 4x4 окружающих пикселей — всего 16. Поскольку они находятся на разных расстояниях от неизвестного пикселя, ближайшие пиксели получают при расчёте больший вес. Бикубическая интерполяция производит значительно более резкие изображения, чем предыдущие два метода, и возможно, является оптимальной по соотношению времени обработки и качества на выходе. По этой причине она стала стандартной для многих программ редактирования изображений (включая Adobe Photoshop), драйверов принтеров и встроенной интерполяции камер.

В вычислительной математике бикубическая интерполяция - расширение кубической интерполяции на случай функции двух переменных, значения которой заданы на двумерной регулярной сетке. Поверхность, полученная в результате бикубической интерполяции, является гладкой функцией, в отличие от поверхностей, полученных в результате билинейной интерполяции или интерполяции методом ближайшего соседа.

Чтобы лучше понять принцип бикубической интерполяции, предлагаю рассмотреть принцип кубической интерполяции.

Если значения функции f(x) и ее производной известны в точках x=0 и x=1, тогда функция может быть интерполирована на интервале [0, 1] используя полином третьего порядка. Формула для вычисления может быть легко получена.

Полином третьего порядка и его производная: (13)

Значения полинома и его производной в точках x=0 и x=1: (14)

Эти четыре тождества могут быть записаны как: (15)

Итак мы получили нашу интерполяционную формулу. На практике алгоритм использует для интерполяции функции, имея некие известные значения в заданных точках. В этом случае мы не можем знать производную функции. Мы могли бы принять производную в заданных точках, как 0, однако для получения более гладких и правдоподобных графиков функций мы примем за производную уклон линии между предыдущей и следующей точкой. Таким образом для расчетов нам понадобится 4 точки. Предположим, мы имеем 4 значения функции в точках p0, p1, p2 и p3, расположенных соответственно на x=-1, x=0, x=1 и x=2. Подставим полученные значения f(0), f(1), f(2) и f(3): (16)

Сопоставив эти данные с полученными ранее формулами мы имеем: (17)

Результат: (18)

Так как бикубическая интерполяция представляет собой кубическую интерполяцию в двух измерениях.

Мы можем, используя формулу кубической интерполяции, полученную выше, построить бикубическую интерполяционную формулу. 

Представим, что нам известно 16 точек p_ij, с точкой начала координат в (i-1, j-1), где i,j изменяются от 0 до 3. Тогда, мы сможем интерполировать поверхность на участке [0,0] х [1,1], для этого интерполируем 4 колонки и потом интерполируем полученные результаты в горизонтальном направлении: