
- •Линейно зависимые и независимые системы векторов
- •3.Базисы на прямой, на плоскости, в пространстве
- •4.Проекция вектора на ось. Свойства проекций. Система координат. Направляющие косинусы
- •5.Скалярное произведение векторов и его свойства
- •6.Векторное произведение векторов и его свойства
- •7.Смешанное произведение векторов и его свойства
5.Скалярное произведение векторов и его свойства
Определение.
Величина
 называется скалярным произведением
векторов
называется скалярным произведением
векторов
 ,
,
 .
.
Обозначение:
 ,
,
 :
:

Очевидно, справедливы соотношения:
 .
.
Свойства скалярного произведения
-
(
 ,
,
 ;
; -
(
 +
+ ;
; -
λ (
 ,
,
 (λ
(λ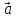 ,
,
 ,
λ
,
λ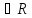 ;
; -
(


 ,
причём (
,
причём ( .
.
Доказательство свойств скалярного произведения
-
Справедливость следует из определения скалярного произведения.
-
(
 +
+ ,
,
 ,
,

-
(λ
 ,
,
 λ
λ
-
Очевидно.
Выпишем полезные результаты:
 ;
;
 ;
;
 .
.
Пусть
известны координаты векторов
 ,
,
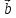 .
.
 ,
,
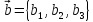 .
.
Вычислим скалярное произведение :
( ,
,
 ,
,
так
как



6.Векторное произведение векторов и его свойства
Определение
1.
Векторы
 образуют правую тройку, если кратчайший
поворот
образуют правую тройку, если кратчайший
поворот
 совершается против часовой стрелки при
наблюдении из конца вектора
совершается против часовой стрелки при
наблюдении из конца вектора
 .
В противном случае векторы
.
В противном случае векторы
 образуют левую тройку (см. рисунок).
образуют левую тройку (см. рисунок).
 -
правая тройка
-
правая тройка  - левая тройка
- левая тройка
















Определение
2.
Векторным произведением векторов
 называется вектор
называется вектор
 ,
такой что
,
такой что
-

-
 ,
,
-
 -
правая тройка векторов.
-
правая тройка векторов.
Обозначение:




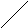




Свойства векторного произведения
-
 .
. -
 .
. -
 .
. -
 .
.
Справедливость свойств 1, 2, 4 следует из определения векторного произведения. Свойство 3 доказано в следующем пункте.
Пусть
известны координаты векторов
 :
:
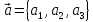 ,
,
 .
.
Утверждение. 

Доказательство.
Очевидно:
 ;
;
 ;
;  ;
; 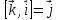
Вычислим
векторное произведение
 :
:



 .
.

▲
Замечания.
-
Утверждение справедливо для случая, когда
 – правая тройка векторов. Везде, где
это специально не оговаривается,
рассматриваем декартовы системы
координат с правой ориентацией тройки
– правая тройка векторов. Везде, где
это специально не оговаривается,
рассматриваем декартовы системы
координат с правой ориентацией тройки
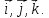
-
 ,
,
где
S
– площадь параллелограмма, построенного
на векторах
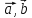 :
:
S
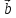


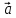

7.Смешанное произведение векторов и его свойства
Определение.
Величина
 называется смешанным произведением
векторов
называется смешанным произведением
векторов
 .
.
Утверждение.

где
V
– объём параллелепипеда, построенного
на векторах
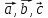 .
.
Доказательство.
Докажем для случая , когда
 - правая тройка.
- правая тройка.
Имеем ( см. рисунок ):

Здесь H – высота параллелепипеда;
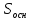 – площадь основания;
– площадь основания;
φ
– угол между вектором
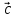 и высотой.
и высотой.

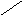
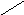


V
φφφ




H






▲
Назовём
циклической перестановкой тройки
 перестановку вида:
перестановку вида:

Справедливо утверждение:
Циклическая
перестановка тройки
 не меняет её ориентации.
не меняет её ориентации.
Следствие.
 .
.
Поэтому
смешанное произведение векторов
обозначают просто:
 .
.
Пусть
известны координаты векторов
 :
:
 ,
,
 ,
,
 .
.
Утверждение (доказать самостоятельно).
 .
.
Следствия.
-
Векторы
 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда

-
Векторы
 образуют правую тройку тогда и только
тогда, когда
образуют правую тройку тогда и только
тогда, когда

Докажем свойтсво 3 векторного произведения.
Лемма.
Пусть
 выполнено (
выполнено ( ,
,
 Тогда
Тогда

Доказательство.
 – любой вектор. Возьмём
– любой вектор. Возьмём
 .
Имеем: (
.
Имеем: (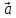 ,
,
 ,
но отсюда
,
но отсюда

▲
Утверждение.

Доказательство. Надо доказать:
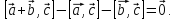
Пусть
 – произвольный вектор. Имеем:
– произвольный вектор. Имеем:
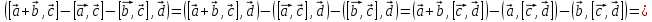

В силу леммы получаем, что утверждение справедливо.
▲
