3.Базисы на прямой, на плоскости, в пространстве

Определение 1.

1. Вектор называется базисом на прямой, если

1) ,

2) , лежащий на этой прямой, можно записать в виде

(1)

3. Векторы образуют базис на плоскости, если

1) образуют линейно независимую систему,

2) 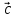, лежащий на плоскости, может быть записан в виде

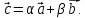(2)

4. Векторы образуют базис в пространстве, если

1. образуют линейно независимую систему,

2. может быть записан в виде

(3)

Теорема 1. Любой ненулевой вектор, лежащий на прямой, образует базис на прямой.

Теорема 2. Любая пара неколлинеарных векторов на плоскости образуют базис на этой плоскости.

Теорема 3. Любая тройка неколлинеарных векторов образует базис в пространстве.

Справедливость теорем 1,2,3 следует из утверждений 1-7, доказанных в предыдущем пункте.

Определение 2. Правые части равенств (1), (2), (3) называются разложениями векторов по базисам ; ; соответственно; числа α, β, γ называются координатами вектора в базисе.

Утверждение 1. Разложение по базису единственно.

Доказательство.

Пусть вектор имеет два разложения в базисе :

Но – базис 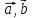является ЛНС .

Аналогично доказывается утверждение для базиса на прямой и в пространстве.

▲

Утверждение 2. При сложении векторов их координаты складываются. При умножении вектора на число все его координаты умножаются на это число.

Доказательство. Проведём доказательство для плоскости. Пусть – два вектора на плоскости, – базис на плоскости:

1)

2) | α

.

▲

Контрольный вопрос

Дана пирамида ABCD.

D

E

C

F

A

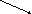
B

Пусть Найдите координаты вектора в базисе , если E, F – середины ребер BD, BC.

Ответ. . Координаты (0, , ).

4.Проекция вектора на ось. Свойства проекций. Система координат. Направляющие косинусы

Определение 1. Назовём осью прямую с заданным направлением:

Определение 2. Векторной проекцией вектора на ось , называется вектор 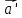, такой, что

1) или 2)

Определение 3. Скалярной проекцией вектора на ось называется величина

,

где φ – угол между векторами , :

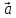
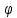
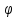
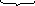
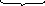
> 0

< 0

= 0

Свойства проекций

1. .

Справедливость этого утверждения следует из рисунка:

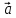
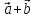
2. , α R

В справедливости можно убедиться, рассмотрев рисунки для случаев

1)α = 0, 2) α < 0, 3) α > 0.

Введём прямоугольную декартову систему координат в пространстве.

Для этого фиксируем точку О – “начало координат” и ортонормированный

базис

.

Направим ось OX вдоль вектора ; ось OY – вдоль вектора ; ось OZ

вдоль вектора . Пусть M – произвольная точка пространства. Разложим вектор

по базису

.

Числа x, y, z называются координатами точки M в системе координат

OXYZ .

Обозначение: M(x, y, z);

Очевидно : .

Z

Y

M

X

Пусть α, β, γ – углы, которые вектор образует с осями OX, OY, OZ. Имеем:

.

Величины называются направляющими косинусами вектора . Очевидно:

.

Пусть A(; B(. Имеем:

Отсюда ( см. рисунок )

A

O

B