
- •Линейно зависимые и независимые системы векторов
- •3.Базисы на прямой, на плоскости, в пространстве
- •4.Проекция вектора на ось. Свойства проекций. Система координат. Направляющие косинусы
- •5.Скалярное произведение векторов и его свойства
- •6.Векторное произведение векторов и его свойства
- •7.Смешанное произведение векторов и его свойства
Лекция 9
Аналитическая геометрия. Векторная алгебра
-
Основные определения.
Линейные операции над векторами
Вектор
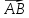 – направленный отрезок, точка A
– начало отрезка, точка В – конец
отрезка:
– направленный отрезок, точка A
– начало отрезка, точка В – конец
отрезка:
A


B
Будем
обозначать векторы :
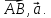
Определение
1.
Вектор
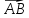 является нулевым вектором, если точки
A
и B
совпадают:
является нулевым вектором, если точки
A
и B
совпадают:
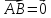 .
.
Определение
2.
Векторы
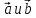 называются коллинеарными,
если, будучи
приведены
к общему началу, они лежат на одной
прямой:
называются коллинеарными,
если, будучи
приведены
к общему началу, они лежат на одной
прямой:
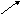


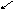



Нулевой
вектор
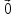 коллинеарен любому вектору.
коллинеарен любому вектору.
Определение
3.
Векторы
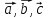 называются компланарными векторами,
если, будучи приведены к общему началу,
они лежат в одной плоскости:
называются компланарными векторами,
если, будучи приведены к общему началу,
они лежат в одной плоскости:









Определение
4.
Длиной вектора
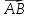 называется длина отрезка AB:
называется длина отрезка AB:
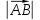 = AB.
= AB.
Определение
5.
Векторы
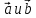 называются равными, если
называются равными, если
-
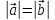 ;
; -
направления векторов
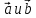 совпадают.
совпадают.
Определение 6. (суммы векторов)
Суммой
векторов
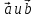 называется вектор
называется вектор
 (обозначается
(обозначается
 ),
который строится либо по правилу
параллелограмма, либо по правилу
треугольника:
),
который строится либо по правилу
параллелограмма, либо по правилу
треугольника:
-
правило параллелограмма:
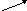
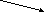
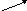

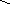



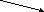


-
правило треугольника:

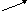

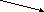




Определение 7. (произведения вектора на число)
Вектор
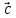 называется произведением вектора
называется произведением вектора
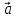 на
действительное число α (обозначается
на
действительное число α (обозначается
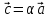 ),
если
),
если
-
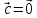 при
α=0,
при
α=0, -
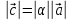 ,
,
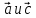 сонаправлены при α>0,
сонаправлены при α>0, -
 ,
,
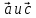 сонаправлены при α<0.
сонаправлены при α<0.
Свойства линейных операций над векторами
-
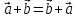 ;
; -
(
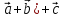 =
=
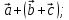
-
α(
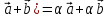 ;
; -
(α+β)
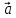 = α
= α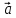 +β
+β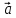 ;
; -
(α
 β)
β)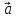 = α(
= α(
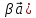 ;
; -
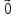 +
+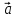 =
=
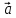 ;
; -
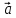 +(
+(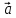 )
=
)
=
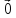 ;
; -
1
 =
=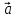 .
.
Справедливость свойств 1÷8 следует из определений линейных операций над векторами. Докажем, например, справедливость свойства 2:







-
Линейно зависимые и независимые системы векторов
Определение
1.
Вектор
вида
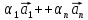 называется линейной комбинацией векторов
называется линейной комбинацией векторов
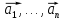 .
.
Здесь
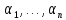
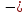 некоторые действительные числа,
называемые коэффициентами линейной
комбинации.
некоторые действительные числа,
называемые коэффициентами линейной
комбинации.
Определение
2. Система
векторов
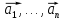 называется линейно зависимой системой
(ЛЗС), если
называется линейно зависимой системой
(ЛЗС), если
 (
(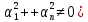 :
:
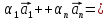
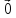 .
(*)
.
(*)
Если
же равенство (*) может быть выполнено
только при
 =
0, то система векторов
=
0, то система векторов
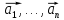 называется линейно независимой системой
(ЛНС).
называется линейно независимой системой
(ЛНС).
Утверждение
1. Система
векторов
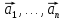 является линейно зависимой системой
тогда и только тогда, когда хотя бы один
из векторов может быть записан в виде
линейной комбинации других векторов.
является линейно зависимой системой
тогда и только тогда, когда хотя бы один
из векторов может быть записан в виде
линейной комбинации других векторов.
Доказательство.
-
Пусть
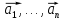 – линейно зависимая система. Тогда
– линейно зависимая система. Тогда
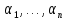 :
:
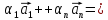
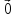 .
.
Пусть
для определённости
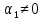 .
Тогда
.
Тогда
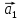 =
—
=
—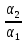
 —
—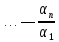
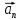 ,
,
то
есть вектор
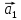 может быть записан в виде линейной
комбинации других векторов системы.
может быть записан в виде линейной
комбинации других векторов системы.
-
Пусть хотя бы один из векторов
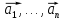 может быть записан в виде линейной
комбинации других. Пусть для определённости
это справедливо для вектора
может быть записан в виде линейной
комбинации других. Пусть для определённости
это справедливо для вектора
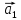 :
:
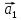 =
—
=
—
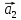 —
—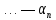
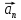 .
.
Перепишем:
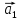 —
—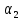
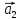 —
—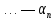
 =
=
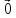 .
.
Справедливо
равенство (*),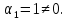 Следовательно, система векторов
Следовательно, система векторов
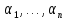 является линейно зависимой системой.
является линейно зависимой системой.
▲
Утверждение 2. Система векторов, содержащая нулевой вектор, является линейно зависимой системой.
Доказательство.
Пусть для определённости
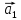 =
=
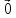 .
.
В
этом случае справедливо равенство (*)
при
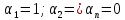 :
:
1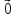 +
+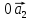 +
+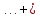 0
0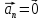 .
.
Следовательно,
система
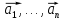 является линейно зависимой системой.
является линейно зависимой системой.
▲
Утверждение 3. Система векторов, содержащая линейно зависимую подсистему, является линейно зависимой.
Доказательство.
Пусть для определённости векторы
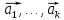 ,
входящие в систему
,
входящие в систему
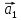 ,
,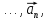 образуют линейно зависимую систему.
Тогда справедливо равенство:
образуют линейно зависимую систему.
Тогда справедливо равенство:
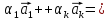
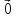 ,
,
причём
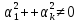 .
.
Следовательно, справедливо равенство:
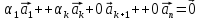 ,
,
в
котором
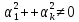 .
Система
.
Система
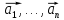 является линейно зависимой.
является линейно зависимой.
▲
Утверждение
4. Векторы
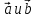 образуют линейно зависимую
образуют линейно зависимую
систему
тогда и только тогда, когда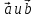 – коллинеарные векторы.
– коллинеарные векторы.
Доказательство.
-
Пусть векторы
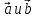 коллинеарны. Следовательно,
коллинеарны. Следовательно,
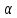 :
:
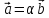 , отсюда, в силу утверждения 1, система
, отсюда, в силу утверждения 1, система
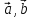 является линейно зависимой системой.
является линейно зависимой системой. -
Пусть векторы
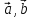 образуют линейно зависимую систему.
Тогда, в силу утверждения 1,
образуют линейно зависимую систему.
Тогда, в силу утверждения 1,
 :
:
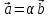 .
Следовательно, векторы
.
Следовательно, векторы
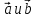 являются коллинеарными.
являются коллинеарными.
▲
Утверждение
5.
Векторы
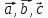 образуют линейно зависимую систему
тогда и только тогда, когда они компланарны.
образуют линейно зависимую систему
тогда и только тогда, когда они компланарны.
Доказательство.
-
Пусть векторы
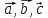 образуют линейно зависимую систему .
В силу утверждения 1, хотя бы один из
векторов может быть записан в виде
линейной комбинации других. Пусть, для
определённости,
образуют линейно зависимую систему .
В силу утверждения 1, хотя бы один из
векторов может быть записан в виде
линейной комбинации других. Пусть, для
определённости,
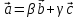 :
:



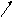





Следовательно,
по определению получаем, что векторы
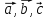 являются
компланарными.
являются
компланарными.
-
Пусть
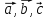 - компланарны.
- компланарны.
2a).
Среди
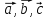 есть коллинеарная пара. В силу утверждения
4 эта пара образует линейно зависимую
систему. В силу утверждения 3 векторы
есть коллинеарная пара. В силу утверждения
4 эта пара образует линейно зависимую
систему. В силу утверждения 3 векторы
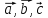 образуют линейно зависимую систему.
образуют линейно зависимую систему.
2б).
Среди векторов
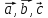 нет коллинеарной пары. Приведём векторы
нет коллинеарной пары. Приведём векторы
 к общему началу:
к общему началу:



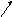





Достроим
параллелограмм с диагональю
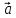 .
Получаем:
.
Получаем:
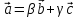 .
В силу утверждения 1 система
.
В силу утверждения 1 система
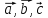 является линейно зависимой системой.
является линейно зависимой системой.
▲
Утверждение 6. Любые 3 вектора на плоскости образуют линейно
зависимую систему.
Доказательство утверждения 6 проводится аналогично тому, как это
было выполнено для утверждения 5.
Утверждение
7.
Любые четыре вектора
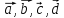 в пространстве
в пространстве
образуют линейно зависимую систему.
Доказательство.
-
Пусть среди векторов
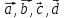 нет некомпланарной тройки. Приведём
векторы
нет некомпланарной тройки. Приведём
векторы
 к общему началу, построим параллелепипед
с диагональю
к общему началу, построим параллелепипед
с диагональю
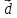 и рёбрами, параллельными векторам
и рёбрами, параллельными векторам
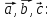


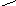

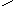


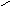



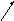
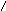
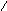



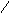


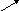
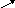
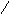

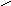




Получили:
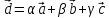 .
В силу утверждения 1 система
.
В силу утверждения 1 система
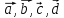 является линейно зависимой.
является линейно зависимой.
-
Пусть среди векторов
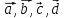 содержится компланарная тройка. Тогда
в силу утверждения 3 система
содержится компланарная тройка. Тогда
в силу утверждения 3 система
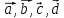 является линейно зависимой.
является линейно зависимой.
▲
