Задача к1

Точка М движется в плоскости ху, при этом заданы уравнения ее движения х = f₁(t) (рис. К1.0 –К1.9) и у = f₂(t) (табл. К1.1) в сантиметрах. Траектория точки на рисунках показана условно. В момент времени t = 2с движущаяся точка М оказывается на своей траектории в какой-то точке Д и со скоростью Vд переходит на другую траекторию – окружность радиуса R=5см, сопряженную с первой. Для второго участка, т.е. для движения по окружности задан закон изменения касательного ускорения а_= f₃(t₁) = 2t₁–1,см/с².

Определить вид и уравнение траектории движения точки на первом участке, ее скорость и ускорение в точке Д, а также радиус кривизны траектории в этой точке. Для второго участка определить положение точки на окружности, соответствующей моменту времени t₁ = 3с, а также скорость, касательное и нормальное ускорения в этой точке Е. При t₁ = 0 движущаяся

точка находилась в месте сопряжения двух траекторий. Построить в масштабе оба участка траектории движения точки М, векторы ее скорости и ускорения в точках Д и Е.

В таблице К1.2 приведены дополнительные данные по касательному ускорению точки а_= f₃(t₁) (в см/с²) для второго участка траектории, с помощью которых варианты задач по усмотрению преподавателя могут быть превращены в трехзначные.

Таблица К1.1

Вариант	0	1	2	3	4
у = f2(t)	3соs(t/6)	6sin(t/3)	4sin2(t/6)	4соs2(t/6)	5соs(t/6)
Вариант	5	6	7	8	9
у = f2(t)	3sin(t/6)	8sin2(t/6)	5sin(t/6)	8соs2(t/6)	6соs(t/3)

Таблица К1.2. Дополнительные данные

Вариант	0	1	2	3	4
а= f3(t1)	2t1 - 1	3t1 + 2	t12 - t1	t1 + 3	2t1 + 1
Вариант	5	6	7	8	9
а= f3(t1)	t1 + 2	t1 - 1	t12 + 1	t1 - 2	t1 + 1

Задача к2

Механизм состоит из ступенчатых колес 1-3, находящихся в зацеплении или связанных ременной передачей, и груза 4, соединенного с колесом 3 с помощью гибкого элемента (троса), как показано на рис. К2.0 – К2.9. Радиусы ступеней колес (в сантиметрах): r₁=4, R₁=10, r₂=5, R₂=12, r₃=8, R₃=16. В зависимости от варианта в таблице К2.1 заданы закон изменения угла поворота одного из колес ₁(₂,₃)=f₁(t) или закон изменения угловой скорости (,) = f₂(t), закон изменения углового ускорения (,) = f₃(t), или закон движения груза 4 s₄=f₄(t).

Угол  выражен в радианах, расстояние s₄ – в сантиметрах, время t – в секундах. Положительное направление для отсчета заданных угловых величин против хода часовой стрелки, а для s₄ – вниз. На каждом из колес указана точка А, В или С, расположенная на большей или меньшей окружности ступени. В начальный момент система находилась в покое. Для момента времени t = 2с определить: скорость груза 4 – V₄, угловую скорость колеса 2 - ₂, угловое ускорение колеса 1 - ₁, ускорение точки С – а_С и количество оборотов, совершенное колесом 1 – z₁. Все полученные величины показать на рисунке с учетом их фактического направления.

В таблице К2.2 приведены необходимые для определения величины, которые могут быть использованы по усмотрению преподавателя. В этом случае варианты задач становятся трехзначными и определять необходимо то, что задано в табл. К2.2, а не по условию.

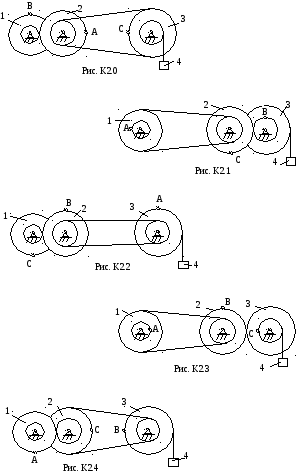
Таблица К2.1

Вариант	0	1	2	3	4
Дано	2=2t2-t3	=3t-1	=3t2-2t	=3t-4t2	1=2t3-3t2
Вариант	5	6	7	8	9
Дано	=8-2t	s4=t2-4t3	3=5t2	=2t2+t	=4+5t

Таблица К2.2. Дополнительные данные

Вариант
0	1	2	3	4	5	6	7	8	9
Определить
V4	VC	VA	VC	VB	VB	V4	VA	VC	V4
2	1	3	2	1	3	1	3	2	1
1	2	1	1	3	2	3	2	1	3
аС	аА	а4	аА	аВ	а4	аВ	а4	аС	аС
z1	z3	z2	z3	z2	z1	z1	z1	z3	z2