3.2 Пример использования Minitab for Windows для построения уравнения регрессии

1 Ввести данные в Minitab for Windows

2 Для проведения корреляционного анализа выбрать команду

StartBasic StatisticCorrelation

3 На экране раскроется диалоговое окно Correlation (Корреляция), представленное на рис. 1

Рис. 1. Диалоговое окно Correlation приложения Minitab

а) в поле Variables ввести значения Y, X1, X2, X3, X4, X5.

б) щелкнуть на кнопке ОК, и на экран будут выведены результаты, представленные в листинге (рис. 2).

Correlations: Y; X1; X2; X3; X4; X5 Y X1 X2 X3 X4 X1 0,676 0,000 X2 0,798 0,228 0,000 0,226 X3 -0,296 -0,222 -0,287 0,112 0,238 0,124 X4 0,550 0,350 0,540 -0,279 0,002 0,058 0,002 0,136 X5 0,618 0,309 0,693 -0,243 0,314 0,000 0,097 0,000 0,195 0,091 Cell Contents: Pearson correlation P-Value

Рис.2 Листинг результата корреляционного анализа в системе Minitab

Корреляционная матрица показывает наличие достаточно тесной связи между зависимой переменной Y и независимыми переменными.

4 Для запуска процедуры анализа регрессии выбрать команду StartRegressionRegression

3 На экране раскроется диалоговое окно Regression (регрессия)

а) в поле Response в качестве зависимой переменной выбрать величину Y

б) в поле Predictors в качестве независимых переменных выбрать величины X1, X2, X3, X4, X5

в) для продолжения работы щелкнуть на кнопке Options. В появившемся окне выбрать Variance inflation factor для расчета степени мультиколлинеарности (фактор роста дисперсии (VIF)).

г) щелкнуть на кнопке ОК, и на экран будут выведены результаты, представленные в листинге (рис. 3).

Regression Analysis: Y versus X1; X2; X3; X4; X5 The regression equation is Y = - 89,7 + 0,202 X1 + 6,12 X2 + 0,113 X3 - 0,005 X4 - 0,50 X5 Predictor Coef SE Coef T P VIF Constant -89,70 17,01 -5,27 0,000 X1 0,20245 0,02813 7,20 0,000 1,237 X2 6,1248 0,9178 6,67 0,000 2,536 X3 0,1135 0,5034 0,23 0,824 1,139 X4 -0,0047 0,7850 -0,01 0,995 1,596 X5 -0,500 1,744 -0,29 0,777 2,082 S = 3,96972 R-Sq = 89,5% R-Sq(adj) = 87,4% Analysis of Variance Source DF SS MS F P Regression 5 3238,09 647,62 41,10 0,000 Residual Error 24 378,21 15,76 Total 29 3616,30 Source DF Seq SS X1 1 1653,15 X2 1 1582,73 X3 1 0,88 X4 1 0,03 X5 1 1,30 Unusual Observations Obs X1 Y Fit SE Fit Residual St Resid 4 31,0 71,000 61,775 1,914 9,225 2,65R 9 48,0 66,000 55,989 1,815 10,011 2,84R R denotes an observation with a large standardized residual.

Рис.3. Листинг результатов регрессионного анализа

Ниже объясняется используемая в приложении Minitab терминология, даются необходимые определения и описываются выполняемые вычисления. Все эти пояснения относятся к содержимому листинга, представленного на рис. 3.

• Coef - коэффициенты регрессии. Найденное уравнение регрессии является следующим:

Y = - 89,7 + 0,202 X1 + 6,12 X2 + 0,113 X3 - 0,005 X4 - 0,50 X5

• R-Sq - уравнение регрессии объясняет 89,5% вариации объема продаж.

• s - стандартная ошибка оценки равна 3,97 ед.. Эта величина является мерой отклонения полученных значений от величин прогноза.

• Т – значение t-статистики. В этом случае большое значение статистики для переменных X1, X2, и малое значение р указывают, что коэффициент при этих переменных значимо отличаются от нуля. Таким образом, коэффициенты при обеих независимых переменных значимо отличаются от нуля.

• Р - значение р = 0,000 равно вероятности получить значение t с абсолютной величиной, не меньшей 7,20, если гипотез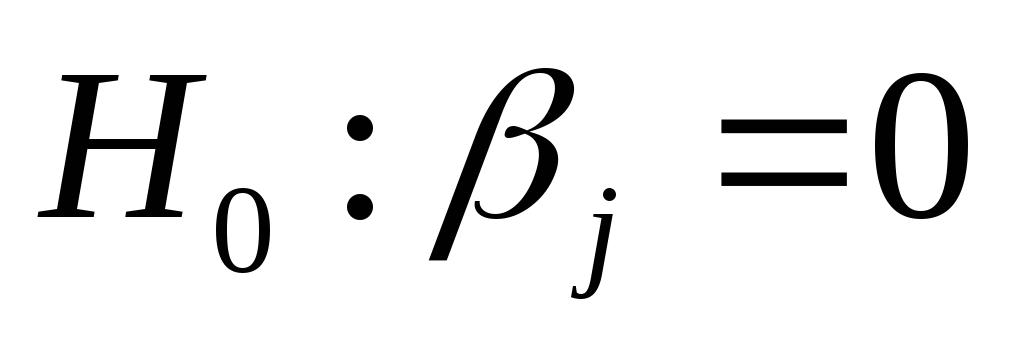а справедлива. Поскольку эта вероятность весьма мала, то гипотеза отклоняется. Коэффициент при переменных X1, X2 значимо отличны от нуля. Коэффициенты же при переменных X3, X4, X5 незначимы

• SS - разложение суммы квадратов, SST=SSR + SSE (общая сумма квадратов = сумма квадратов регрессии + сумма квадратов ошибок).

• F - вычисленное значение F (41,10) используется для проверки значимости регрессии. Табличное значение F-статистики с числом степеней свободы df=5, 24 при уровне значимости 5% равно 2,62. Следовательно, регрессия значима. Функция регрессии объясняет значительную часть изменчивости Y.

• R-Sq(adj) - скорректированный коэффициент детерминации.

• Значение VIF для переменных Х2 и Х5 говорит о наличии мультиколлинеарности.

Последовательно избавляясь от незначимых переменных в уравнении регрессии (повторяя шаг 3 для оставшихся переменных) получим итоговое уравнение (листинг представлен на рис. 4)

Regression Analysis: Y versus X1; X2 The regression equation is Y = - 86,8 + 0,200 X1 + 5,93 X2 Predictor Coef SE Coef T P VIF Constant -86,79 12,35 -7,03 0,000 X1 0,19973 0,02456 8,13 0,000 1,055 X2 5,9314 0,5596 10,60 0,000 1,055 S = 3,75361 R-Sq = 89,5% R-Sq(adj) = 88,7% Analysis of Variance Source DF SS MS F P Regression 2 3235,9 1617,9 114,83 0,000 Residual Error 27 380,4 14,1 Total 29 3616,3 Source DF Seq SS X1 1 1653,2 X2 1 1582,7 Unusual Observations Obs X1 Y Fit SE Fit Residual St Resid 4 31,0 71,000 61,755 1,242 9,245 2,61R 9 48,0 66,000 55,660 0,687 10,340 2,80R R denotes an observation with a large standardized residual.

Рис.4 Листинг результатов регрессионного анализа (итоговый)

Таким образом, полученное уравнение регрессии объясняет 89,5% вариации параметра Y. Мультиколлинеарность переменных отсутствует. По t-статистике коэффициенты уравнения регрессии значимы, по F-статистике уравнение также значимо.

5 Чтобы получить графики остатков, выбрать команду Stats Regression Residual plots. Графики остатков представлены на рисунке 5.

Выбросы

Выбросы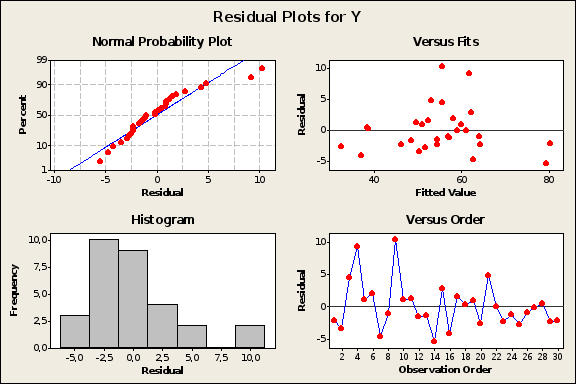

Рис.5 Графики остатков

Анализ графиков также свидетельствует, что уравнение регрессии адекватно описывает взаимосвязь между объемами продаж за месяц (Y), результатами теста способностей (X1) и возрастом продавцов (X2).

Рост результатов теста способностей на единицу приводит к росту объема продаж на 0,2 единицы, увеличение возраста исполнителя на единицу (внутри исследуемого интервала значений Х2) приводит к росту объема продаж на 5,93 единицы.

6 Результат автокорреляционного анализа остатков представлен на рис. 6

Так как все значения автокорреляции близки к нулю и находятся в доверительном интервале, можно сделать вывод о случайности (независимости) остатков. Следовательно, уравнение регрессии можно использовать для интерпретации имеющихся данных.

7 Для определения прогнозного объема продаж необходимо подставить требуемые значения в уравнение регрессии:

Y = - 86,8 + 0,200 X1 + 5,93 X2 =-86,8+0,200*83+5,93*25 = 78,05 ед.

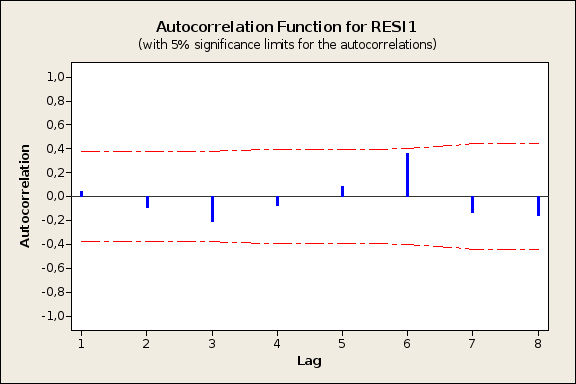
Рис.6 Автокорреляционный анализ остатков

Т.е. при найме на работу сотрудника прошедшего тест на способности на 83 балла возрастом 25 лет, можно ожидать, что ежемесячный объем продаж составит 78,05 ед.

Интервальный прогноз можно получить, воспользовавшись теоретическими положениями, изложенными в п. 2.4.5.

7 Для запуска процедуры пошаговой регрессии выбрать команду StatRegressionStepwise.

8 На экране появится диалоговое окно Stepwise Regression, показанное на рис. 7

Puc. 7 Диалоговое окно Stepwise Regression приложения Minitab

а) зависимая переменная (Response) содержится в столбце С1, озаглавленном Y;

б) независимые переменные содержатся в столбцах С2-С6, озаглавленных X1, X2, X3, X4, X5

в) чтобы ввести значение уровня значимости, щелкнуть на кнопке Methods

9 На экране раскроется диалоговое окно Stepwise-Methods, показанное на рис. 8.

Рис. 8. Диалоговое окно Stepwise-Method приложения Minitab

а) поскольку в расчетах используется уровень значимости 0,05, изменить значения в полях Alpha to enter и Alpha to remove с 0,15 на 0,05

б) щелкнуть на кнопке ОК, а затем еще раз на кнопке ОК в диалоговом окне Stepwise Regression. На экран будут выведены результаты, представленные на рис. 9.

Stepwise Regression: Y versus X1; X2; X3; X4; X5 Alpha-to-Enter: 0,05 Alpha-to-Remove: 0,05 Response is Y on 5 predictors, with N = 30 Step 1 2 Constant -100,85 -86,79 X2 6,97 5,93 T-Value 7,01 10,60 P-Value 0,000 0,000 X1 0,200 T-Value 8,13 P-Value 0,000 S 6,85 3,75 R-Sq 63,70 89,48 R-Sq(adj) 62,41 88,70 Mallows Cp 57,3 0,1

Рис. 9 Листинг результатов пошаговой регрессии в приложении Minitab

По рис. 9 видно, что переменная возраста вводится в уравнение регрессии первой и объясняет 63,7% дисперсии значений объема продаж. Поскольку значение р, равное 0,0000, меньше величины , переменная возраста добавляется в модель. На втором этапе в уравнение регрессии вводится переменная, характеризующая результаты теста способностей. В этом случае уравнение регрессии объясняет 89,48% вариации продаж. Коэффициенты регрессий при переменных значительно отличаются от нуля, и вероятность того, что это происходит лишь в результате случайного отклонения почти нулевая.

Следовательно, уравнение регрессии примет вид:

Y = - 86,8 + 5,93 X2 + 0,200 X1