2.8 Регрессионная диагностика и анализ остатков

Регрессионный анализ будет неполон, пока мы не убедимся, что выбранная модель адекватно представляет данные. Непременно следует проверить адекватность найденной модели до того, как она станет частью методики принятия решений.

Исследование остатков - это важный момент в определении адекватности модели. Несколько графиков остатков, строящихся для проверки предположений о модели регрессии, были предложены в Методических указаниях к проведению лабораторной работы №5. Кроме того, если модели регрессии используются с данными временных рядов, важно вычислить автокорреляции остатков для проверки условия их независимости. Выводы (и решения), сделанные по моделям, не соответствующим основным регрессионным предположениям, могут оказаться совершенно ошибочными. Например, можно заключить, что какие-то изменения независимой переменной приведут к нужным изменениям зависимой переменной, что на самом деле окажется не так. Может быть сделан вывод, что прогноз с большой надежностью (с доверительной вероятностью 0,95) будет не более чем на 2% отличаться от будущего значения зависимой переменной, тогда как фактически доверительная вероятность окажется намного меньше, и т.д.

Рассмотрим некоторые дополнительные способы оценки регрессионной модели. Эти способы направлены на выделение наблюдений, крайних в наборе или представляющих собой выбросы (т.е. наблюдений, заметно отличающихся по значению от остальных данных). Выбросы часто скрываются процессом подгонки и не могут быть достаточно просто определены при исследовании графика остатков. Тем не менее, они могут оказывать существенное влияние на выбор подходящей регрессионной функции. Необходимо тщательно изучать выбросы для того, чтобы принять обоснованное решение, следует ли их оставить в наборе данных или удалить из него. И если их оставлять, то следует определить, как лучше поступить - или влияние выбросов на функцию регрессии должно быть уменьшено, или функция регрессии должна быть подправлена.

Мера влияния i-й точки данных на положение функции регрессии измеряется значением рычага . Значение рычага зависит только от независимых переменных и не зависит от зависимой переменной Y. Для простой линейной регрессии с одной независимой переменной X:

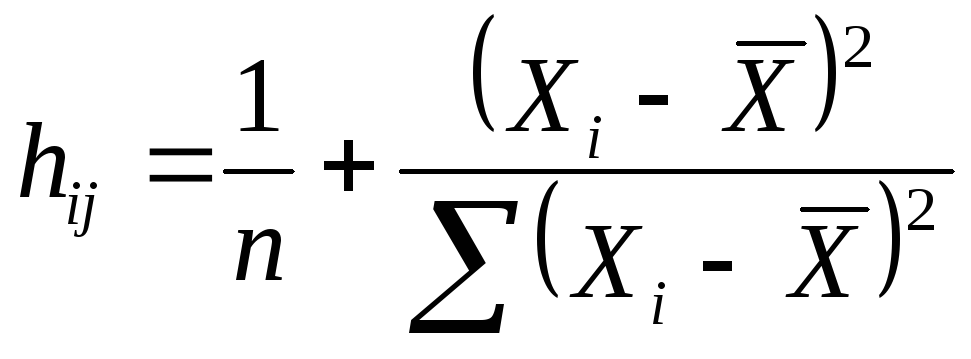
Для k независимых переменных выражение для i-го рычага сложнее; однако, можно показать, что 0 << 1 и его среднее значение равно .

Если i-я точка данных имеет большое значение рычага ( близко к 1), прогноз, для этого значения X почти полностью определяется величиной Y, при очень малом влиянии других данных. Точка с большим значением рычага также размещается на графике на удалении от остальных X (и от их комбинаций). Эмпирически установленное правило утверждает, что может считаться достаточно большим, если .

Определение выбросов или крайних значений Y основывается на размерах остатков . Большие остатки показывают, что значение Y находится далеко от его прогноза, вычисленного по уравнению регрессии. Большая величина остатка будет выделяться на гистограмме остатков как значение, удаленное от нуля (в любом направлении). На графике зависимости остатков от значений прогноза большой остаток будет выделяться как точка, удаленная вверх или вниз от горизонтальной оси.

Пакеты программ, подобные приложению Minitab, отмечают флажком точки данных с крайними значениями Y, вычисляя "стандартизованные" остатки и выделяя точки с большими значениями стандартизованных остатков.

Один метод стандартизации основан на том, что оценки стандартных отклонений остатков равны:

где - стандартная ошибка оценки, a - значение рычага, связанное i-й точкой данных. Тогда стандартизованный остаток равен:

Все стандартизованные остатки имеют дисперсию 1. Стандартизованный остаток считается большим (а значение соответствующей зависимой переменной - крайним), если

Значения Y, соответствующие точкам данных с большими стандартизованными остатками, могут очень сильно повлиять на расположение прямой регрессии.