
- •Математика для технических специальностей
- •Якутск 2005
- •Рекомендации по выполнению и оформлению контрольных работ Цель курса – научить студентов применению математики в специальных дисциплинах и изучении практических явлений.
- •Программа курса
- •Глава 1. Линейная и векторная алгебра ([1] Гл.: 9 п. 1-8, 10, гл.: 14 п.6 пп. 1, 2)
- •Глава 2. Аналитическая геометрия ([1] Гл.: 3, 9 пп. 9 – 14)
- •Глава 3. Введение в математический анализ. Дифференциальное исчисление функции одной переменной ([1] Гл.: 1, 2, 4 – 6)
- •Глава 4. Интегральное исчисление функции одной переменной ([1] Гл.: 7, 8)
- •Глава 5. Дифференциальное и интегральное исчисление функции нескольких переменных ([1] Гл.: 12, 13)
- •Глава 6. Дифференциальные уравнения ([1] Гл.: 15)
- •Глава 7. Теория рядов ([1] Гл. 14)
- •Дифференциальное исчисление функции одной переменной ([2] Гл.6, 7)
- •Исчисление функции нескольких переменных ([2] Гл. 8, [3] Гл. 1,2)
- •Основная литература
- •Оглавление
Дифференциальное исчисление функции одной переменной ([2] Гл.6, 7)
Задача 1. Доказать, что:
1.![]() 2.
2.
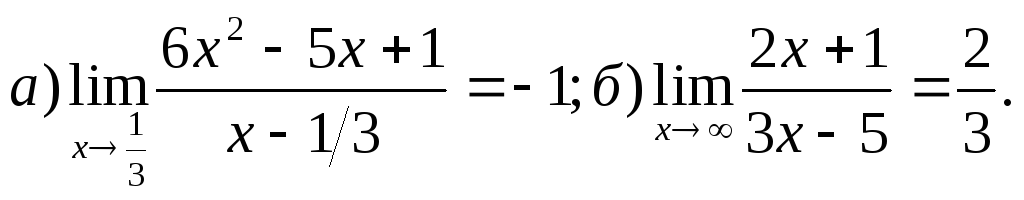
3.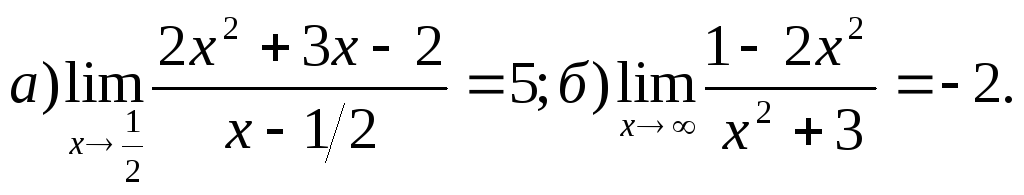 4.
4.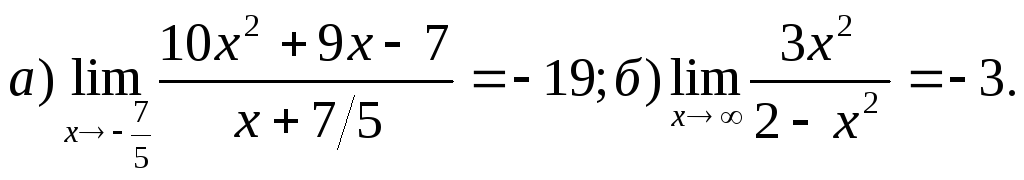
5.
 6.
6.
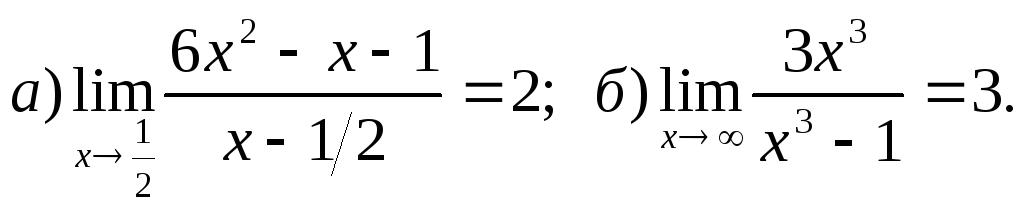
7.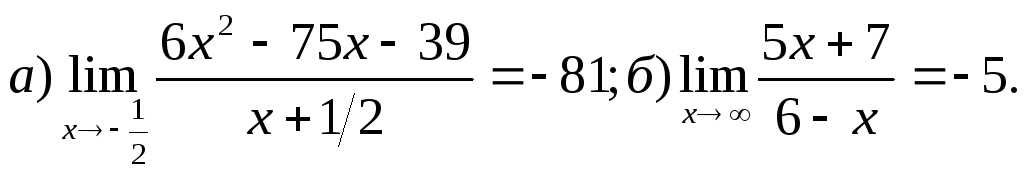 8.
8.
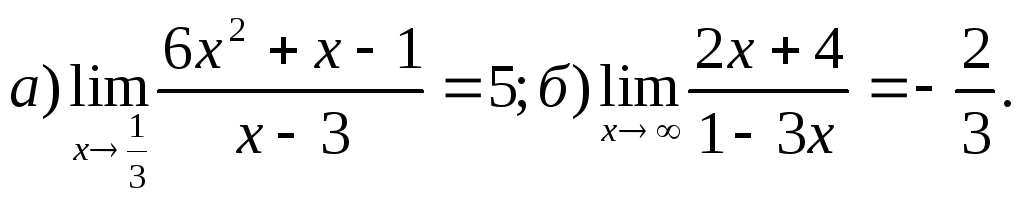
9.
![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.
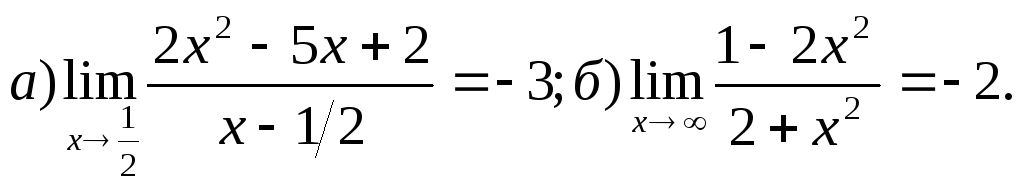 14.
14.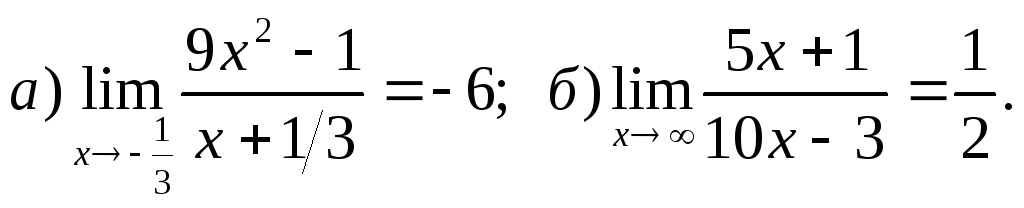
15.
![]() 16.
16.
17.
![]() 18.
18.![]()
19.
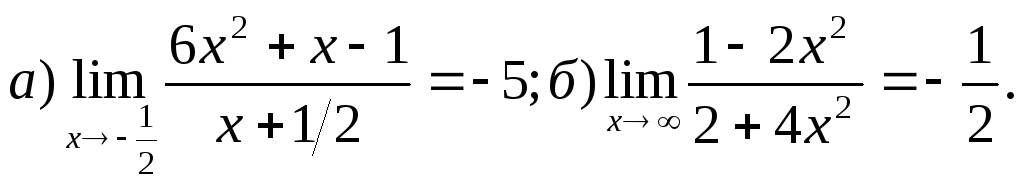 20.
20.
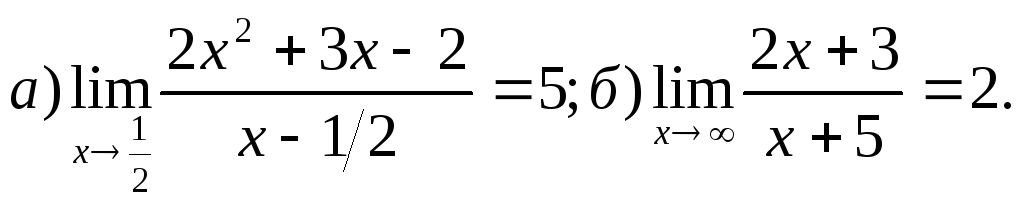
Задача 2. Вычислить пределы функций, не пользуясь правилом Лопиталя.
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
5.
![]()
![]()
6.
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
![]()
![]()
10.
![]()
![]()
11.
![]()
![]()
12.
![]()
![]()
13.
![]()
![]()
14.
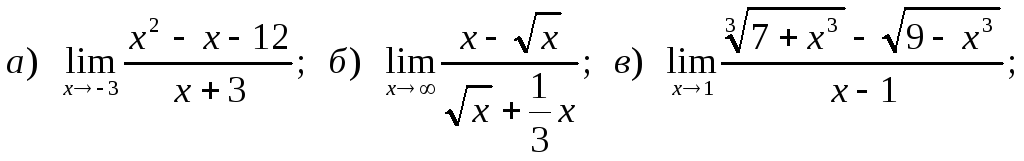
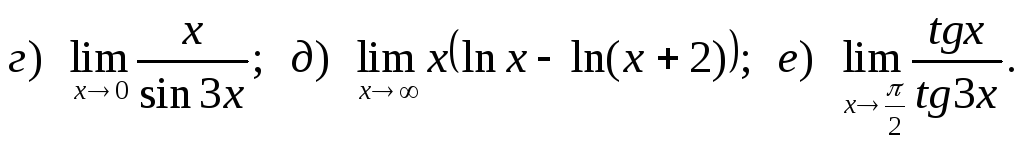
15.
![]()
![]()
16.
![]()
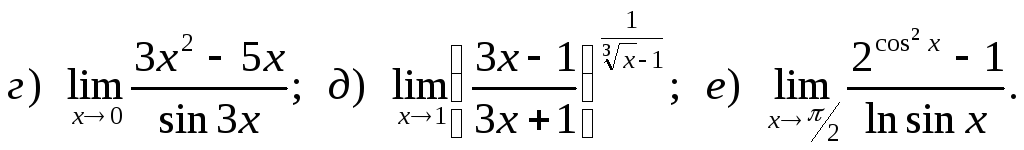
17.
![]()
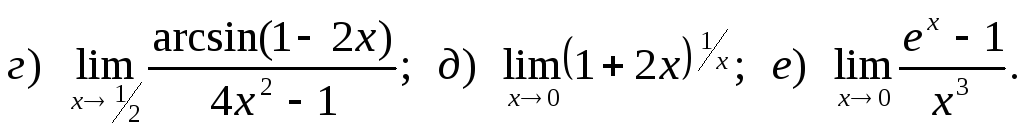
18.
![]()
![]()
19.
![]()
![]()
20.
![]()
![]()
Задача 3.
Доказать, что функция
![]() непрерывна в точке
непрерывна в точке
![]() (найти
(найти
![]() )
и, исходя из определения производной,
найти производную
)
и, исходя из определения производной,
найти производную
![]() в точке
в точке
![]() .
.
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]() 15.
15.
![]()
16.
![]() 17.
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
Задача 4. Найти производные функций.
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
5.
![]()
![]()
6.
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
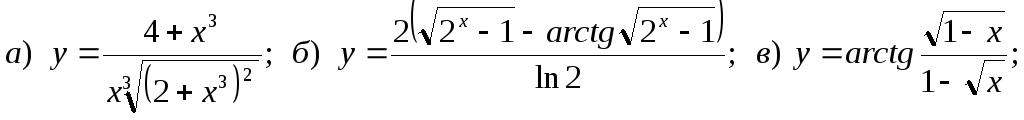
![]()
10.
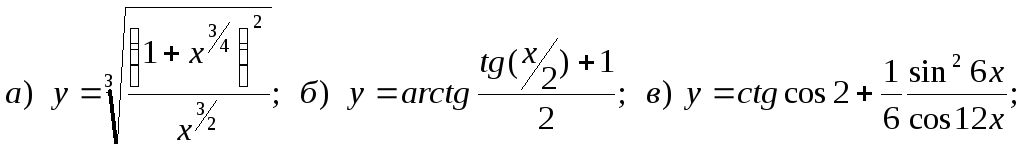
![]()
11.
![]()
![]()
12.
![]()
![]()
13.
![]()
![]()
14.
![]()
![]()
15.
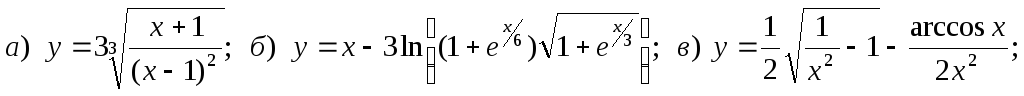
![]()
16.
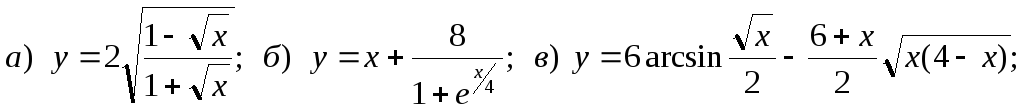
![]()
17.
![]()
![]()
18.
![]()
![]()
19.

![]()
20.
![]()
![]()
Задача 5. Провести полное исследование функций методами дифференциального исчисления и построить их графики.
1.
![]() 2.
2.
![]()
3.
![]() 2.
2.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
Задача 6 ([3] Гл. 3, п.7). а). Начертить в комплексной плоскости линии, точки которых удовлетворяют заданным уравнениям.
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
б). Определить, какие множества точек удовлетворяют заданным неравенствам.
11.
![]() 12.
12.
![]() 13.
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]() 17.
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
Контрольная работа 4. Неопределенный и определенный интегралы
([2] Гл. 9, 10)
Задача 1. Найти неопределенный интеграл.
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
5.
![]()
![]()
6.
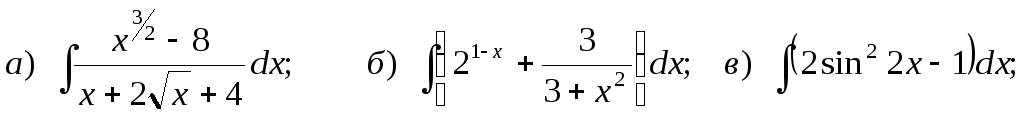
![]()
7.
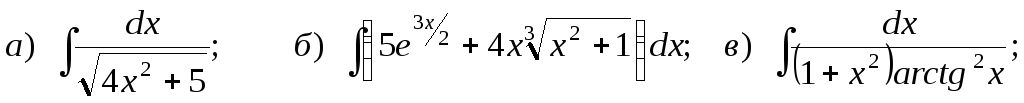
![]()
8.
![]()
![]()
9.
![]()
![]()
10.
![]()
![]()
11.
![]()
![]()
12.

![]()
13.
![]()
![]()
14.
![]()
![]()
15.
![]()
![]()
16.
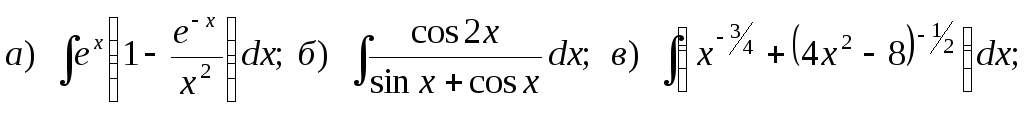
![]()
17.
![]()
![]()
18.
![]()
![]()
19.
![]()
![]()
20.
![]()
![]()
Задача 2. Найти неопределенный интеграл.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
Задача 3. Нарисовать область, ограниченную данными линиями, и вычислить её площадь.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.![]()
5.![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.![]()
11
![]() 12.
12.
![]()
13.![]() 14.
14.
![]()
15.![]() 16.
16.
![]()
17.
![]() 18.
18.
![]() 19.
19.
![]() 20.
20.
![]()
Задача 4.
Вычислить объёмы тел, образованных
вращением фигуры, (вокруг осей
![]() ,
,
![]() ),
ограниченной заданными линиями.
),
ограниченной заданными линиями.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
Задача 5. Нарисовать дугу кривой и вычислить её длину.
1.
![]()
![]()
![]()
2.
![]()
![]()
![]()
3.
![]()
![]()
![]()
4.
![]()
![]()
![]()
5.
![]()
![]()
![]()
6.
![]()
![]()
![]()
7.
![]()
![]()
![]()
8.
![]()
![]()
![]()
9.
![]()
![]()
![]()
10.
![]()
![]()
![]()
11.
![]()
![]()
![]()
12.
![]()
![]()
![]()
13.
![]()
![]()
![]()
14.
![]()
![]()
![]()
15.
![]()
![]()
![]() 16.
16.
![]()
![]()
![]()
17.
![]()
![]()
![]()
18.
![]()
![]()
![]()
19.
![]()
![]()
![]()
20.
![]()
![]()
![]()
Контрольная работа 5. Дифференциальное и интегральное
