3. Эквивалентность и преобразование формул

Введем на множестве M отношения следования и эквивалентности.

Формула B следует из формулы A (обозначается AB), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.

Формула A эквивалентна формуле B (обозначается A~B), если они следуют друг из друга, то есть AB и BA. Легко показать, что это определение эквивалентно определению, введенному в п.1.

Теорема 3.1. Формула B следует из формулы A тогда и только тогда, когда тождественно истинна формула AB.

Теорема 3.2. Формула A эквивалентна формуле B тогда и только тогда, когда тождественно истинна формула A~B.

Эквивалентность формул является отношением эквивалентности, поэтому множество M можно разбить на классы эквивалентности, включив в один класс эквивалентные между собой формулы. Каждой формуле U соответствует класс эквивалентности, который обозначается [U].

Теорема 3.3. Если A есть некоторая подформула формулы U и A эквивалентна формуле B, то формула, полученная заменой A в формуле U на B, эквивалентна U. Иными словами, если A~B, то U(A) ~ U(B).

Например, так как AB ~ , то (AB)C ~ C.

Следствие. Если U~A и V~B, то:

1) UV ~ AB;

2) UV ~ AB;

3) UV ~ AB;

4) (U~V) ~ (A~B);

5) U ~ A.

Теорема 3.3 и ее следствие позволяют преобразовывать формулы, упрощая их, и доказывать эквивалентность формул. Приведем список основных тавтологий, выражающих свойства логических операций.

1. Коммутативность:

X Y ~ Y X, X Y ~ YX.

2. Ассоциативность:

(X Y)Z ~ X (YZ), (XY)Z ~ X(YZ).

3. Идемпотентность:

XX ~ X, XX ~ X.

4. Законы поглощения:

XXY ~ X, X(XY) ~ X.

5. Взаимная дистрибутивность конъюнкции и дизъюнкции:

X (YZ) ~ (X Y)(X Z), X (YZ) ~ (XY)(XZ).

6. Свойства констант:

XЛ ~ Л, XИ ~ X, XИ ~ И, XЛ ~ X.

7. Законы де Моргана:

, .

8. Закон двойного отрицания:

.

9. Закон противоречия:

 Л.

10. Закон исключенного третьего:

 И.

Тождественная истинность всех формул (кроме законов поглощения) уже доказана непосредственно построением таблиц истинности.

Задание. Доказать 1-й из законов поглощения.

Решение.

.

Приведем еще несколько эквивалентностей, имеющих широкое применение.

11. .

12. .

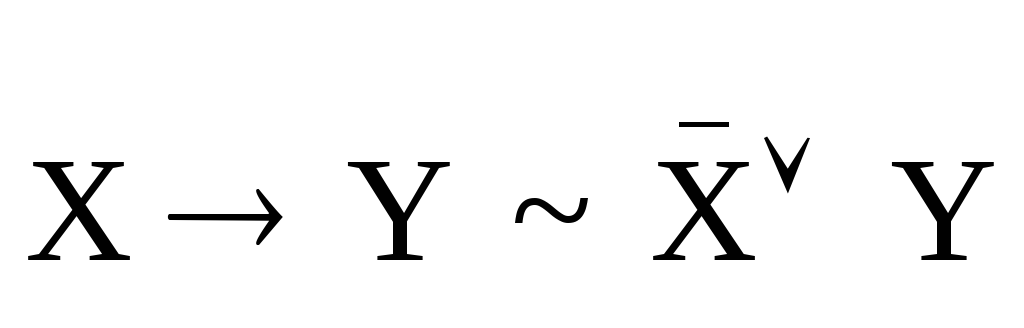13. Склеивание:

, .

Формула называется приведенной, если она содержит операции конъюнкции, дизъюнкции и операцию отрицания, относящуюся к высказывательным переменным.

Теорема 3.4. Каждый класс эквивалентности [U] может быть представлен приведенной формулой, т.е. для любой формулы U M существует приведенная формула V.

Приведенная формула для данного класса эквивалентности не является единственной. Определим порядок построения приведенной формулы.

1. Удаляются операции импликация и эквиваленция по формулам 11, 12.

2. Операции отрицания спускаются до высказывательных переменных с помощью законов де Моргана и двойного отрицания.

3. Если это возможно, то полученная приведенная формула упрощается с помощью свойств 3, 4, 5, 6, 9, 10.

Таким образом, проверить эквивалентность формул, тождественную истинность и ложность формулы или упростить ее можно с помощью этого алгоритма.

Задание. Упростить формулу .

Решение. () ~

~ () ~ () ~ A.

Формула U^* называется двойственной к приведенной формуле U, если она получена заменой операций конъюнкции на дизъюнкции и наоборот.

Теорема 3.5 (принцип двойственности). Пусть U() – приведенная формула, тогда

U^*() ~ U().

В автоматическом управлении и при эксплуатации вычислительных ма­шин приходится иметь дело с переключательными схемами (релейно-контакт­ными, полупроводниковыми), состоящие из сотен реле, полупроводников, маг­нитных элементов. Переключательная схема состоит из переключателей (на­пример, кнопочные устройства, электромагнитные реле, полупроводниковые элементы и т.п.) и соединяющих их проводников. При конструировании таких схем существенную помощь может оказать алгебра высказываний: можно по­строить схему, выполняющую требуемые функции (синтезирование схемы) или изучить действие построенной схемы и возможно ее упростить (анализ схемы).

Каждой схеме ставится в соответствие формула алгебры высказываний, и каждая формула реализуется с помощью некоторой схемы. Покажем, как уста­новить такое соответствие. Каждому переключателю P ставится в соответствие высказывательная переменная P, которая истинна тогда и только тогда, когда переключатель P замкнут. Схеме с последовательным соединением переключа­телей P и Q соответствует формула, являющаяся конъюнкцией высказаватель­ных переменных, соответствующих этим переключателям, . Схеме с параллель­ным соединением переключателей P и Q соответствует формула, являющаяся дизъюнкцией высказавательных переменных, соответствующих этим переклю­чателям, . Два переключателя P и могут быть связаны так, что когда P замкнут, то разомкнут. Тогда переключателю ставится в соответствие переменная , являющаяся отрицанием P.

Задание. Упростить схему

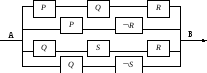
Решение. Запишем формулу, соответствующую схеме, по приведенным выше правилам

U = .