
- •2. Аналитическая геометрия в пространстве
- •2.1. Системы координат в пространстве
- •Векторная алгебра
- •2.2. Векторы
- •2.3. Скалярное произведение
- •2.4. Векторное произведение векторов
- •2.5. Смешанное произведение трех векторов
- •Прямая и плоскость в пространстве
- •2.6. Плоскость в пространстве
- •2.7. Прямая в пространстве
- •2.8. Взаимное расположение плоскости и прямой в пространстве
- •2.9. Задачи на составление уравнения плоскости
- •2.10. Поверхности второго порядка
2.7. Прямая в пространстве
-
Общие уравнения прямой. Любую прямую в пространстве можно задать как линию пересечения двух не параллельных плоскостей, т.е. (совместной) системой двух линейных уравнений
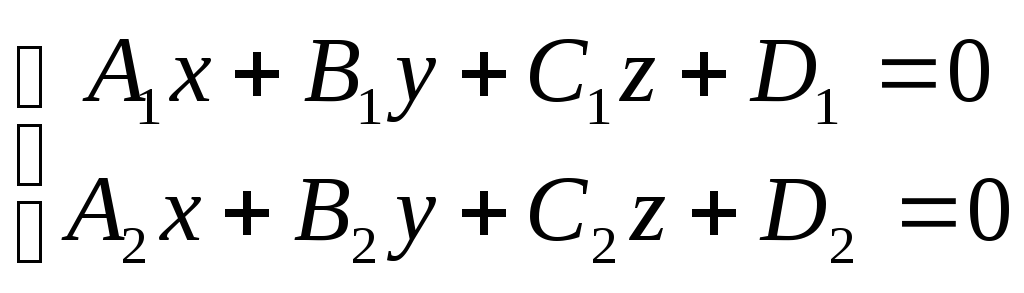 . .(1)
. .(1)
Например,
система уравнений
![]() задает прямую в пространстве, так как
коэффициенты этих уравнений не
пропорциональны и, следовательно,
плоскости не параллельны, т.е. пересекаются
по прямой.
задает прямую в пространстве, так как
коэффициенты этих уравнений не
пропорциональны и, следовательно,
плоскости не параллельны, т.е. пересекаются
по прямой.
-
Канонические уравнения прямой. Положение прямой в пространстве можно задать с помощью точки
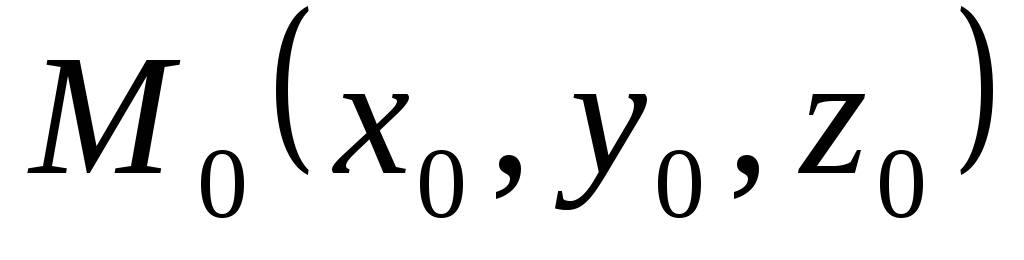 ,
через которую проходит прямая, и
направляющего
вектора
,
через которую проходит прямая, и
направляющего
вектора
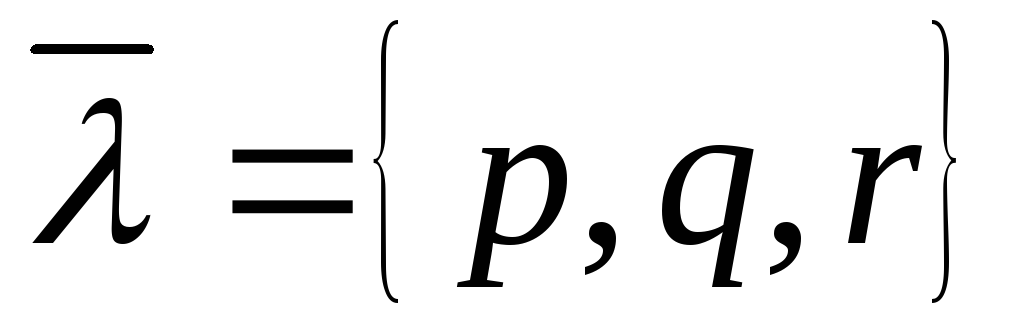 ,
параллельного прямой. Тогда рассматриваемая
прямая определяется уравнениями
,
параллельного прямой. Тогда рассматриваемая
прямая определяется уравнениями
![]() , (2)
, (2)
которые называют каноническими уравнениями прямой.
Пример 1.
Составить канонические уравнения
прямой, проходящей через точку М0(1, -2, 0)
и параллельной вектору
![]() .
.
Ответ:
![]() .
.
Замечание.
В
случае, когда какая-нибудь из координат
направляющего вектора равна нулю,
принято писать равенства (2)
с нулем (или с двумя нулями) в знаменателе;
такая запись становится символической,
но ею пользуются ввиду ее наглядности.
Например, запись
![]() означает, что прямая проходит через
точку М0(2, 0, -3)
и параллельна вектору
означает, что прямая проходит через
точку М0(2, 0, -3)
и параллельна вектору
![]() (т.е. параллельна оси Oy).
(т.е. параллельна оси Oy).
От
записи (1) можно перейти к записи (2),
находя из системы (1) какую-нибудь точку
рассматриваемой прямой и беря в качестве
направляющего вектора
![]() векторное произведение нормальных
векторов двух непараллельных плоскостей:
векторное произведение нормальных
векторов двух непараллельных плоскостей:
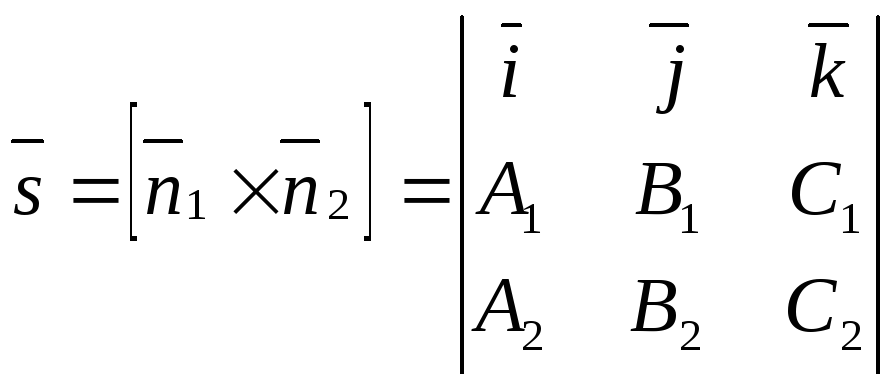 .
Этот вектор перпендикулярен
.
Этот вектор перпендикулярен
![]() и
и
![]() ,
т.е. параллелен линии пересечения данных
плоскостей, является направляющим для
заданной прямой.
,
т.е. параллелен линии пересечения данных
плоскостей, является направляющим для
заданной прямой.
Пример 2.
Прямая задана уравнениями
![]() .
Получить канонические уравнения этой
прямой.
.
Получить канонические уравнения этой
прямой.
Решение.
Так как коэффициенты данных уравнений
не пропорциональны, плоскости не
параллельны, т.е. пересекаются по
некоторой прямой. Найдем какую-нибудь
точку, лежащую на прямой. Например,
полагая
![]() ,
из системы
,
из системы
![]() находим
находим
![]() ,
,
![]() .
Получаем точку (3, 1, 0). Теперь найдем
направляющий вектор
.
Получаем точку (3, 1, 0). Теперь найдем
направляющий вектор
 .
.
Ответ:
канонические уравнения прямой
![]() .
.
-
Уравнения прямой, проходящей через две данные точки
 и
и
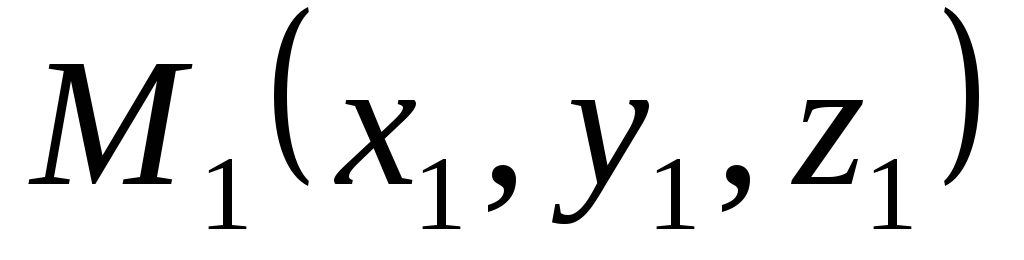 .
Беря в качестве точки, через которую
проходит прямая, точку
.
Беря в качестве точки, через которую
проходит прямая, точку
 ,
а в качестве направляющего вектора
,
а в качестве направляющего вектора
 вектор
вектор
 ,
запишем канонические
уравнения прямой:
,
запишем канонические
уравнения прямой:
![]() .
.
Пример 3.
Записать
канонические уравнения прямой, проходящей
через точки
![]() и
и
![]() .
.
Ответ:
![]() .
.
Замечание.
Полученные
уравнения показывают, что прямая
перпендикулярна оси Oz
(так как проекция направляющего вектора
на ось Oz
равна нулю). Кроме того, видно, что прямую
можно представить как линию пересечения
двух плоскостей: плоскости
![]() (или
(или
![]() ),
которая параллельна оси Oz,
и плоскости
),
которая параллельна оси Oz,
и плоскости
![]() (или
(или
![]() ,
т.е.
,
т.е.
![]() ),
параллельной осям Ox
и
Oy.
),
параллельной осям Ox
и
Oy.
-
Параметрические уравнения прямой. Если приравнять каждую из дробей в равенствах (2) параметру t, получим следующие параметрические уравнения прямой:
 .
.
Когда
действительная переменная t
(параметр) пробегает интервал
![]() ,
текущая точка
,
текущая точка
![]() пробегает всю прямую. Например, для
прямой из Примера 3 будем иметь
пробегает всю прямую. Например, для
прямой из Примера 3 будем иметь
![]() ,
,
![]() ,
,
![]() ,
откуда получаем параметрические
уравнения
,
откуда получаем параметрические
уравнения
 .
.
-
Угол между двумя прямыми в пространстве. Очевидно, этот угол
 равен углу между направляющими векторами
равен углу между направляющими векторами
 и
и
 данных прямых. Поэтому его можно найти
из формулы
данных прямых. Поэтому его можно найти
из формулы
 .
.
Ясно,
что необходимое и достаточное условие
перпендикулярности
двух прямых имеет вид
![]() или
или
![]() ,
а условие
параллельности
–
,
а условие
параллельности
–
![]() .
.
Пример 4.
Найти угол между прямыми
![]() и
и
![]() .
.
Решение.
Здесь
![]() ,
,
![]() ,
поэтому
,
поэтому
![]() .
.
Отсюда
![]() ;
второй из углов, образованных прямыми,
равен
;
второй из углов, образованных прямыми,
равен
![]() .
.
Пример 5.
Одна прямая задана каноническими
уравнениями
![]() ,
а другая – параметрическими уравнениями
,
а другая – параметрическими уравнениями
 .
Убедиться, что эти прямые параллельны.
.
Убедиться, что эти прямые параллельны.
Решение.
Направляющий вектор первой прямой
![]() ,
а второй
,
а второй
![]() .
Координаты этих векторов пропорциональны:
.
Координаты этих векторов пропорциональны:
![]() ,
поэтому прямые параллельны.
,
поэтому прямые параллельны.
Пример 6.
Составить параметрические уравнения
прямой, проходящей через точку М0(-1, 2, 0)
и перпендикулярной прямым
![]() и
и
![]() .
.
Решение.
Так как направляющий вектор
![]() прямой должен быть перпендикулярен
обеим прямым, в качестве
прямой должен быть перпендикулярен
обеим прямым, в качестве
![]() можно взять векторное произведение
направляющих векторов данных прямых:
можно взять векторное произведение
направляющих векторов данных прямых:
 .
.
Ответ:
параметрические уравнения прямой имеют
вид
 .
.
