2.4. Векторное произведение векторов

• Определение. Векторным произведением вектора на вектор 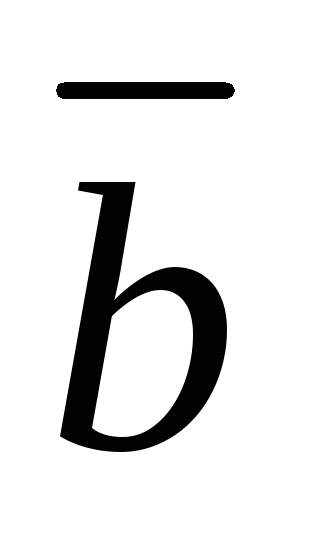называется вектор, который мы будем обозначать символом 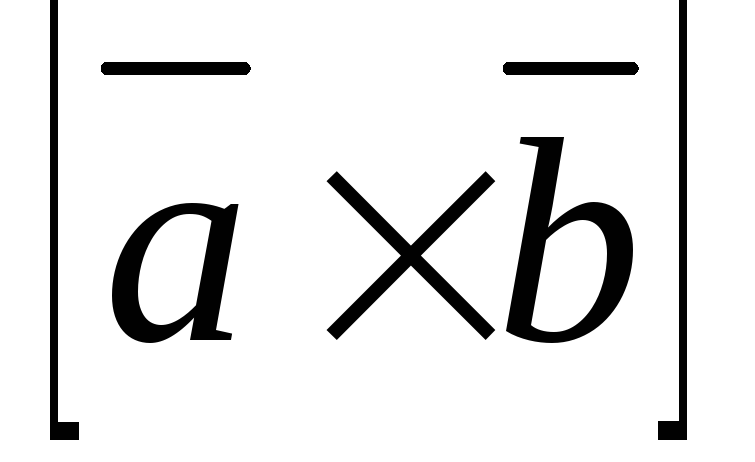и который определяется следующими тремя условиями:

1. модуль вектора равен площади параллелограмма, построенного на векторах и (если они приведены к общему началу), т.е. равен , где – угол между и ;

2. вектор перпендикулярен к и к ;

3. вектор относительно векторов и 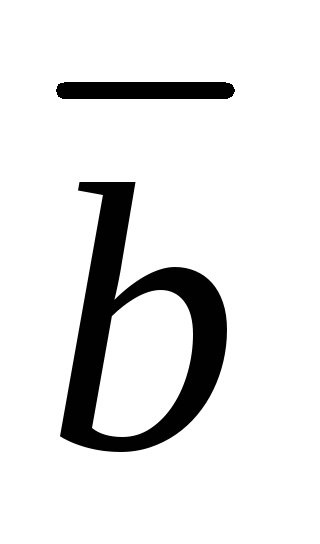направлен так же, как ось Oz направлена относительно осей Ox и Oy (образуют правую тройку).

Если векторы , , приведены к общему началу, то вектор должен быть направлен так, чтобы из его конца кратчайший поворот вектора к был виден против часовой стрелки.

Рис. 26.

• Свойства векторного произведения.

1)

2)

3) (где – скаляр).

Отсюда можно сделать вывод, что при перемножении векторных многочленов можно поступать так же, как при перемножении обычных многочленов. Однако следует помнить, что (в отличие от скалярного произведения) при перестановке сомножителей меняется знак.

В качестве примеров нахождения векторного произведения можно получить следующие векторные произведения ортов осей координат:

, , .

Из определения векторного произведения вытекает, что если и коллинеарны, то их векторное произведение равно нулю. Например,

, , .

• Выражение векторного произведения через координаты сомножителей. Если в декартовой прямоугольной системе координат заданы векторы 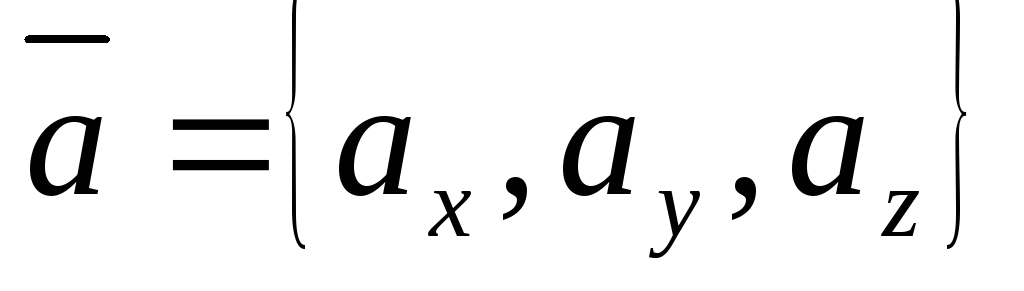и , то .

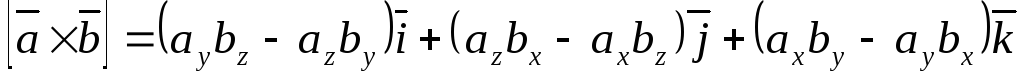Для облегчения запоминания этой формуле обычно придают такой вид:

.

Пример 1. Угол между векторами и равен 30°. Найти площадь параллелограмма, построенного на векторах и , если длина вектора равна 5, а вектора равна 4.

Решение. Найдем векторное произведение (здесь учтено, что векторные произведения коллинеарных векторов и , а также и равны нулевому вектору, и свойства 1 и 2 векторного произведения). Так как модуль векторного произведения равен площади параллелограмма, то искомая площадь равна .

Ответ: 100 кв. ед.

Пример 2. Найти площадь треугольника ABC с вершинами , , .

Решение. Сначала найдем векторы

,

.

Теперь найдем векторное произведение

.

Модуль этого вектора равен площади параллелограмма, построенного на векторах и . Искомая площадь в два раза меньше, т. е. равна

.

Ответ: кв. ед.

Пример 3. Найти координаты единичного вектора, перпендикулярного векторам и .

Решение. Найдем векторное произведение

.

Полученный вектор, согласно определению векторного произведения, перпендикулярен заданным векторам и , но его длина равна не единице, a . Единичный же вектор получится, если все координаты найденного вектора разделить на его длину.

Ответ: (можно также взять вектор, противоположный найденному).

2.5. Смешанное произведение трех векторов

• Определение. Смешанным произведением векторов ,,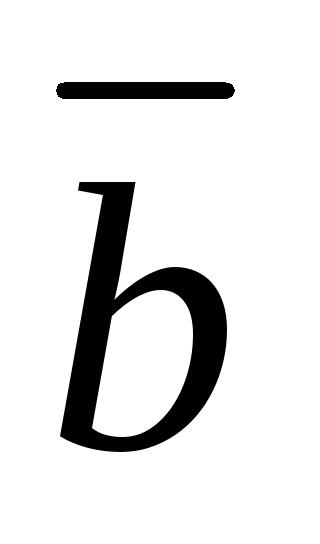 называется число .

• Геометрический смысл смешанного произведения. Смешанное произведение

представляет собой число, абсолютная величина которого равна объему параллелепипеда, построенного на перемножаемых векторах (если эти векторы приведены к общему началу и некомпланарны – см. рис. 27).

Рис. 27.

Смешанное произведение положительно, если векторы ,, образуют правую тройку, и отрицательно, если левую. Заметим, что объем пирамиды MNPQ, построенной на векторах ,,, в шесть раз меньше объема упомянутого параллелепипеда.

• Свойства смешанного произведения.

1) Из геометрического смысла смешанного произведения следует, что ; это позволяет обозначать смешанное произведение символом .

2) При перестановке любых двух сомножителей смешанное произведение меняет знак:

, , .

3) При циклической перестановке сомножителей (т.е. при перестановке сомножителей согласно схеме ) смешанное произведение не изменяется:

.

• Необходимое и достаточное условие компланарности трех векторов ,, состоит в равенстве нулю их смешанного произведения:

(1)

(или, иначе говоря, смешанное произведение трех векторов равно нулю тогда и только тогда, когда эти векторы компланарны).

• Выражение смешанного произведения через координаты перемножаемых векторов. Пусть , , 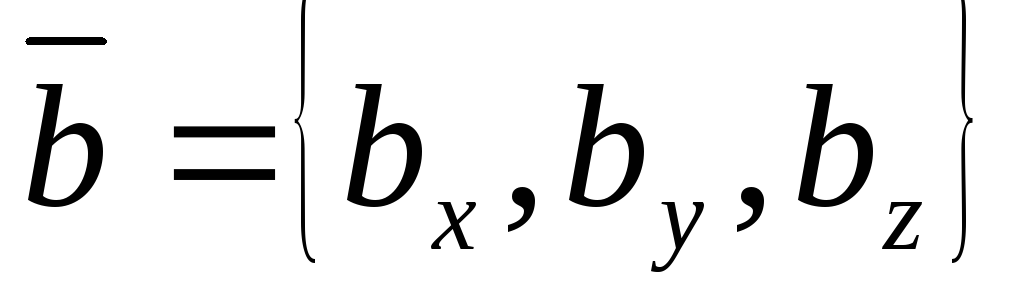. Тогда смешанное произведение равно такому определителю третьего порядка:

. (2)

Из (1) следует, что необходимое и достаточное условие компланарности трех векторов состоит в равенстве нулю определителя третьего порядка, составленного из координат этих векторов. К аналогичному равенству сводится необходимое и достаточное условие того, что четыре точки M,N,P,Q (см. рис. 27) лежат в одной плоскости.

Пример 1. Найти объем параллелепипеда, построенного на векторах

, , .

Решение. Найдем смешанное произведение данных векторов по формуле (2):

.

Отрицательный знак смешанного произведения свидетельствует о том, что векторы ,, образуют левую тройку. Объем параллелепипеда равен .

Ответ: 28 куб. ед.

Пример 2. Найти объем треугольной пирамиды, если даны координаты ее вершин М(1, -1, -1), N(2, -3, -4), P(5, -4, -6), Q(0, 5, 4).

Решение. Находим координаты трех векторов:

, , .

Вычислим теперь по формуле (2) смешанное произведение этих векторов:

.

Тогда объем параллелепипеда, построенного на трех рассматриваемых векторах, равен , а искомый объем треугольной пирамиды MNPQ – в шесть раз меньше.

Ответ: куб. ед.

Пример 3. Лежат ли точки М(-4, 5, 2), N(-10, 11, -2), Р(0, 1, 0), Q(-l, 2, -3) в одной плоскости?

Решение. Найдем координаты трех векторов:

, , . Вычислим определитель, составленный из координат этих векторов:

. Как сказано выше, этот факт означает, что данные точки M, N, P, Q лежат в одной плоскости.