
- •2. Аналитическая геометрия в пространстве
- •2.1. Системы координат в пространстве
- •Векторная алгебра
- •2.2. Векторы
- •2.3. Скалярное произведение
- •2.4. Векторное произведение векторов
- •2.5. Смешанное произведение трех векторов
- •Прямая и плоскость в пространстве
- •2.6. Плоскость в пространстве
- •2.7. Прямая в пространстве
- •2.8. Взаимное расположение плоскости и прямой в пространстве
- •2.9. Задачи на составление уравнения плоскости
- •2.10. Поверхности второго порядка
Прямая и плоскость в пространстве
2.6. Плоскость в пространстве
-
Векторное уравнение плоскости. Пусть плоскость проходит через точку
 и перпендикулярна
вектору
и перпендикулярна
вектору
 .
Для произвольной точки плоскости
.
Для произвольной точки плоскости
 ("текущей
точки") векторы
("текущей
точки") векторы
 и
и
 должны быть перпендикулярны.
Отсюда получаем векторное
уравнение плоскости
должны быть перпендикулярны.
Отсюда получаем векторное
уравнение плоскости
![]() .
.
Здесь
![]() – ненулевой
вектор, который называют нормальным
вектором плоскости
(рис. 28).
– ненулевой
вектор, который называют нормальным
вектором плоскости
(рис. 28).
В координатной форме уравнение плоскости принимает вид
![]() . (1)
. (1)

Пример 1.
Составить уравнение
плоскости, проходящей через точку
![]() (-1, 0, 2)
и перпендикулярной
вектору
(-1, 0, 2)
и перпендикулярной
вектору
![]() .
.
Решение. Искомое уравнение имеет
вид
![]() .
.
Рис. 28.
-
Общее уравнение плоскости. Уравнению (1) можно придать вид
![]() . (2)
. (2)
Это уравнение первой степени с тремя переменными, в котором хотя бы один из коэффициентов А,В,С отличен от нуля. Оно называется общим уравнением плоскости.
Любая плоскость определяется уравнением вида (2). Рассмотрим частные случаи общего уравнения плоскости.
-
При
 уравнение принимает вид
уравнение принимает вид
 ;
такая плоскость проходит
через начало координат.
;
такая плоскость проходит
через начало координат. -
При
 ,
,
 ,
,
 уравнение плоскости
уравнение плоскости
 – плоскость
параллельна
оси Ох
(и
проходит через нее, если
– плоскость
параллельна
оси Ох
(и
проходит через нее, если
 ).
). -
При
 ,
,
 ,
,
 уравнение плоскости
уравнение плоскости
 – плоскость
параллельна
оси Оy
(и
проходит через нее, если
– плоскость
параллельна
оси Оy
(и
проходит через нее, если
 ).
). -
При
 ,
,
 ,
,
 уравнение плоскости
уравнение плоскости
 – плоскость
параллельна
оси Оz
(и
проходит через нее, если
– плоскость
параллельна
оси Оz
(и
проходит через нее, если
 ).
). -
При
 ,
,
 ,
,
 уравнение плоскости
уравнение плоскости
 – плоскость
параллельна
плоскости хOy
(в
частности,
– плоскость
параллельна
плоскости хOy
(в
частности,
 – уравнение плоскости хOy).
– уравнение плоскости хOy). -
При
 ,
,
 ,
,
 уравнение плоскости
уравнение плоскости
 – плоскость
параллельна
плоскости xОz
(в
частности,
– плоскость
параллельна
плоскости xОz
(в
частности,
 – уравнение плоскости хOz).
– уравнение плоскости хOz). -
При
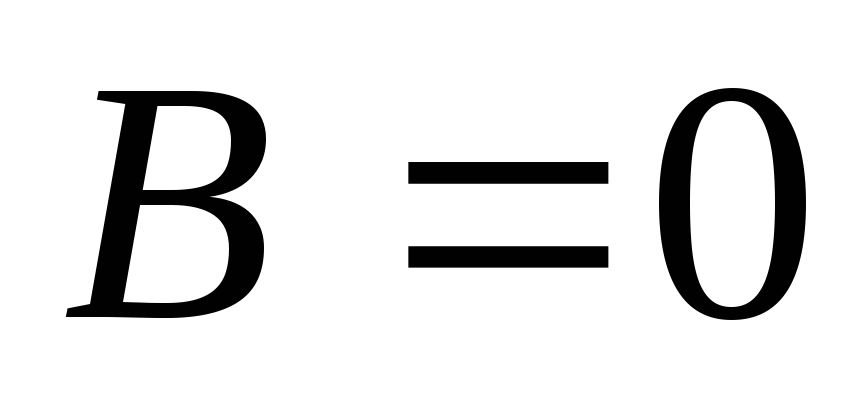 ,
,
 ,
,
 уравнение плоскости
уравнение плоскости
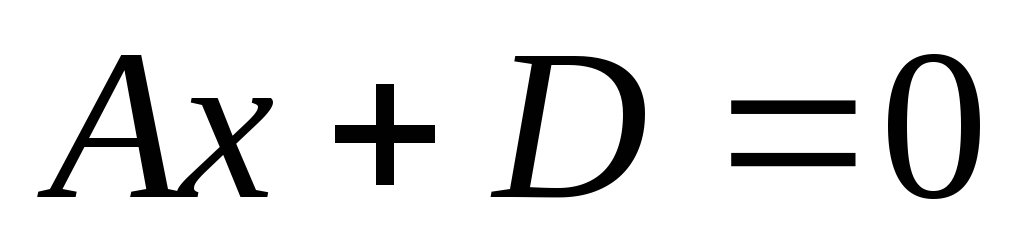 – плоскость
параллельна
плоскости yОz
(в
частности,
– плоскость
параллельна
плоскости yОz
(в
частности,
 – уравнение плоскости yOz).
– уравнение плоскости yOz).
Для построения плоскости на чертеже достаточно получить какие-нибудь три точки данной плоскости. Чаще всего находят точки пересечения плоскости с осями координат (если плоскость не параллельна ни одной из осей).
Пример 2.
Построить
плоскость, заданную уравнением
![]() .
.
Решение.
а)
положим
![]() ,
,
![]() ,
тогда
,
тогда
![]() ;
получаем точку пересечения плоскости
с осью
Ох:
Р(2, 0, 0);
б) положим
;
получаем точку пересечения плоскости
с осью
Ох:
Р(2, 0, 0);
б) положим
![]() ,
,
![]() ,
тогда
,
тогда
![]() ;
получаем точку пересечения плоскости
с осью Оу:
Q(0, 3, 0);
в) положим
;
получаем точку пересечения плоскости
с осью Оу:
Q(0, 3, 0);
в) положим
![]() ,
,
![]() ,
тогда
,
тогда
![]() ;
получаем точку пересечения плоскости
с осью Оz:
R(0, 0, 6).
Для наглядного изображения плоскости
остается соединить отрезками
прямых три полученные точки Р,
Q,
R
(рис. 29, а).
;
получаем точку пересечения плоскости
с осью Оz:
R(0, 0, 6).
Для наглядного изображения плоскости
остается соединить отрезками
прямых три полученные точки Р,
Q,
R
(рис. 29, а).
Пример
3. Построить
плоскость, заданную уравнением
![]() .
.
Решение.
а)
положим
![]() ,
,
![]() ,
тогда
,
тогда
![]() ;
получим точку пересечения плоскости с
осью
Ох:
Р(2, 0, 0);
б) положим
;
получим точку пересечения плоскости с
осью
Ох:
Р(2, 0, 0);
б) положим
![]() ,
,
![]() ,
тогда
,
тогда
![]() ;
получим точку пересечения плоскости с
осью Оz:
R(0, 0, 3).
Соединим отрезком прямой точки P
и R,
после чего нетрудно представить себе,
как выглядит данная плоскость (рис.
29, б).
;
получим точку пересечения плоскости с
осью Оz:
R(0, 0, 3).
Соединим отрезком прямой точки P
и R,
после чего нетрудно представить себе,
как выглядит данная плоскость (рис.
29, б).

Рис. 29.
-
Уравнение плоскости в отрезках на осях. Если (а, 0, 0), (0, b, 0), (0, 0, с) – точки пересечения плоскости с осями Ох, Оу, Oz соответственно (здесь а,b,с не равны нулю), то уравнению такой плоскости можно придать форму
![]() . (3)
. (3)
Это
"уравнение
плоскости в отрезках".
Эта
форма уравнения плоскости особенно
удобна для построения плоскости на
чертеже. Если в уравнении (2) коэффициенты
и свободный член не равны нулю, можно
записать его в виде
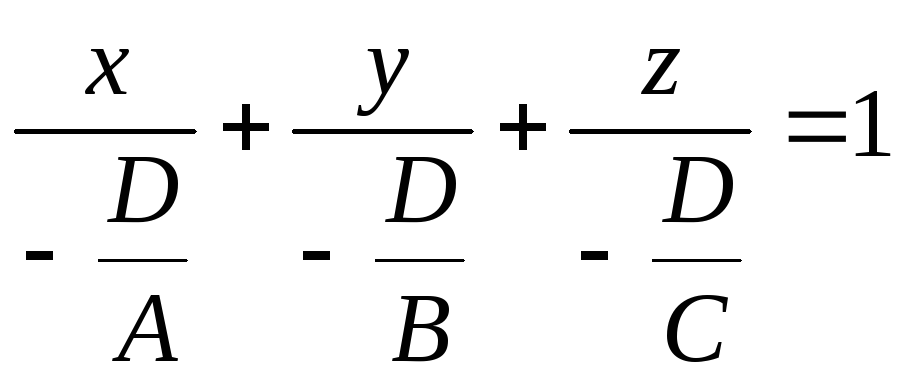 ,
т.е. придать ему форму (3).
,
т.е. придать ему форму (3).
-
Нормальное уравнение плоскости. Аналогично тому, как это делалось для уравнения прямой на плоскости (см. п.1.6.), общее уравнение плоскости
 можно привести к нормальному виду,
деля его на число
можно привести к нормальному виду,
деля его на число
 ,
где знак перед корнем берется
противоположным знаку свободного члена
D.
,
где знак перед корнем берется
противоположным знаку свободного члена
D.
Для
нахождения расстояния от данной точки
![]() до данной плоскости
до данной плоскости
![]() надо привести уравнение плоскости к
нормальному виду, а затем подставить в
левую часть нормального уравнения
плоскости координаты
надо привести уравнение плоскости к
нормальному виду, а затем подставить в
левую часть нормального уравнения
плоскости координаты
![]() данной точки М.
Тогда искомое расстояние равно абсолютной
величине полученного при этом числа h,
т.е. равно
данной точки М.
Тогда искомое расстояние равно абсолютной
величине полученного при этом числа h,
т.е. равно
![]() .
.
Замечание.
Если
![]() ,
т.е. если плоскость не проходит через
начало координат, то при h<0
точка М и начало координат лежат по одну
сторону от данной плоскости, а при h>0
– по разные стороны (при h=0,
очевидно, точка М лежит на плоскости).
,
т.е. если плоскость не проходит через
начало координат, то при h<0
точка М и начало координат лежат по одну
сторону от данной плоскости, а при h>0
– по разные стороны (при h=0,
очевидно, точка М лежит на плоскости).
Пример 4.
Найти расстояние от точки М(1, 2, 3)
до плоскости
![]() .
.
Решение.
1) Приводим уравнение плоскости к
нормальному виду, деля его на
![]() (знак плюс взят потому, что
(знак плюс взят потому, что
![]() ):
):
![]() ;
;
2)
Подставляя в левую часть этого уравнения
![]() ,
,
![]() ,
,
![]() ,
получим число
,
получим число
![]() .
Таким образом, искомое расстояние равно
.
Таким образом, искомое расстояние равно
![]() .
Тот факт, что
.
Тот факт, что
![]() ,
свидетельствует о том, что точки М
и О
лежат по разные стороны от заданной
плоскости.
,
свидетельствует о том, что точки М
и О
лежат по разные стороны от заданной
плоскости.
Пример 5.
Найти расстояние между двумя параллельными
плоскостями
![]() и
и
![]() .
.
Решение.
Возьмем произвольную точку на первой
плоскости, например, точку М(0, -1, 0).
Искомое расстояние равно, очевидно,
расстоянию от точки М
до второй плоскости, т.е.
![]() .
.
Ответ:
![]() .
.
-
Угол между двумя плоскостями. Пусть две плоскости заданы общими уравнениями
![]() ,
,
![]() . (4)
. (4)
Угол
![]() между их нормальными векторами
между их нормальными векторами
![]() и
и
![]() равен (двугранному) углу между данными
плоскостями. Поэтому угол между
плоскостями можно найти из формулы
равен (двугранному) углу между данными
плоскостями. Поэтому угол между
плоскостями можно найти из формулы
![]()
(см.
формулу (4) из п. 2.3.). Это угол
![]() лежит в пределах от 0 до
лежит в пределах от 0 до
![]() ;
другой двугранный угол, образованный
двумя пересекающимися плоскостями,
равен
;
другой двугранный угол, образованный
двумя пересекающимися плоскостями,
равен
![]() .
.
-
Условие перпендикулярности двух плоскостей. Две данные плоскости (4) перпендикулярны тогда и только тогда, когда
 ,
т.е. при выполнении условия
,
т.е. при выполнении условия
![]() или
или
![]()
(см. формулу (5) из п. 2.3.).
Например,
плоскости
![]() и
и
![]() перпендикулярны, так как
перпендикулярны, так как
![]() .
.
Две
данные плоскости параллельны
тогда и только тогда, когда их нормальные
векторы
![]() и
и
![]() коллинеарны, т.е. при выполнении условия
коллинеарны, т.е. при выполнении условия
![]() .
.
Здесь, как и в п.2.3, при равенстве нулю какого-нибудь из знаменателей следует считать равным нулю и соответствующий числитель.
Например,
плоскости
![]() и
и
![]() параллельны, так как
параллельны, так как
![]() .
Заметим дополнительно, что если
выполняются равенства
.
Заметим дополнительно, что если
выполняются равенства
![]() ,
то это говорит о том, что плоскости
совпадают, т.е. уравнения (4) определяют
одну и ту же плоскость.
,
то это говорит о том, что плоскости
совпадают, т.е. уравнения (4) определяют
одну и ту же плоскость.
Пример 6.
Составить уравнение плоскости, которая
проходит через точку М0(1, -1, 0)
и параллельна плоскости
![]() .
.
Решение.
Так как у нужной нам плоскости, очевидно,
тот же самый нормальный вектор {2, 3, -4},
что и у заданной плоскости, то искомое
уравнение должно иметь вид
![]() или
или
![]() – ответ.
– ответ.
Пример 7.
Найти угол между плоскостями, заданными
уравнениями
![]() и
и
![]() .
.
Решение.
Находим косинус угла
![]() между нормальными векторами
между нормальными векторами
![]() и
и
![]() :
:
![]() ;
;
отсюда
![]() .
Это один из двугранных углов, образованных
плоскостями; другой угол равен
.
Это один из двугранных углов, образованных
плоскостями; другой угол равен
![]() .
.
-
Уравнение пучка плоскостей. Все плоскости, проходящие через линию пересечения двух (не параллельных) данных плоскостей (4) ("пучок плоскостей"), представляются уравнением вида
![]() ,
,
где p
и q
– произвольные числа, не равные нулю
одновременно. Придавая p
и q
конкретные значения, получаем уравнение
той или иной плоскости, проходящей через
прямую, по которой пересекаются две
данные плоскости. Например, при
![]()
![]() получим уравнение первой плоскости, а
при
получим уравнение первой плоскости, а
при
![]()
![]() – уравнение второй плоскости.
– уравнение второй плоскости.
Пример 8.
Составить уравнение плоскости, проходящей
через линию пересечения двух плоскостей
![]() и
и
![]() и через начало координат.
и через начало координат.
Решение. Искомое уравнение содержится в уравнении пучка плоскостей
![]() ,
,
где p
и q
– некоторые числа, причем
![]() (в противном случае это уравнение дало
бы плоскость
(в противном случае это уравнение дало
бы плоскость
![]() ,
которая не проходит через начало
координат). Поэтому искомое уравнение
можно записать в виде
,
которая не проходит через начало
координат). Поэтому искомое уравнение
можно записать в виде
![]() .
.
Требование,
чтобы плоскость проходила через начало
координат, приводит к равенству
![]() ,
откуда
,
откуда
![]() .
Таким образом, искомое уравнение имеет
вид
.
Таким образом, искомое уравнение имеет
вид
![]() или
или
![]() – ответ.
– ответ.
Замечание. Множество всех плоскостей, проходящих через заданную точку называется связкой плоскостей.
