
- •2. Аналитическая геометрия в пространстве
- •2.1. Системы координат в пространстве
- •Векторная алгебра
- •2.2. Векторы
- •2.3. Скалярное произведение
- •2.4. Векторное произведение векторов
- •2.5. Смешанное произведение трех векторов
- •Прямая и плоскость в пространстве
- •2.6. Плоскость в пространстве
- •2.7. Прямая в пространстве
- •2.8. Взаимное расположение плоскости и прямой в пространстве
- •2.9. Задачи на составление уравнения плоскости
- •2.10. Поверхности второго порядка
2. Аналитическая геометрия в пространстве
2.1. Системы координат в пространстве
-
Декартова прямоугольная система координат. Эта система координат определяется заданием трех взаимно перпендикулярных осей (пересекающихся в одной точке О – начале координат) и единицы масштаба. Оси обычно обозначают Ox, Oy, Oz. Имеет место взаимно однозначное соответствие между точками пространства и тройками чисел x, y, z – координатами точек.

Замечание. Различают правые и левые системы декартовых координат.
-
Расстояние d между двумя точками пространства
 и
и
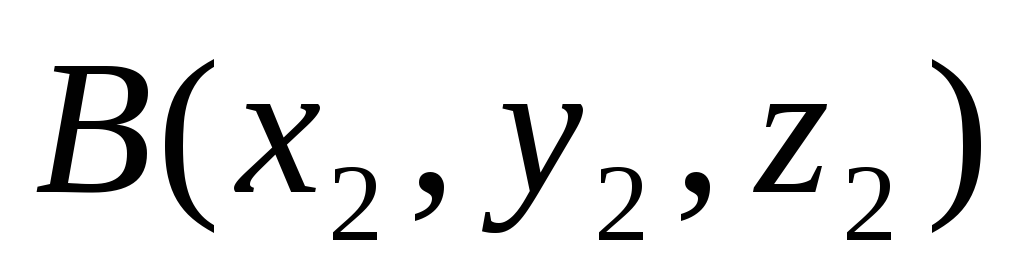 (т.е. длина отрезка АВ) вычисляется
по формуле
(т.е. длина отрезка АВ) вычисляется
по формуле
![]() .
.
В частности, расстояние от точки
![]() до начала координат равно
до начала координат равно
![]() .
.
Пример 1. Расстояние между точками
A(-3, 1, 5) и B(-2, 0, 4)
равно
![]() ,
а длина отрезка ОА равна
,
а длина отрезка ОА равна
![]() .
.
-
Деление отрезка в данном отношении. Пусть даны точки
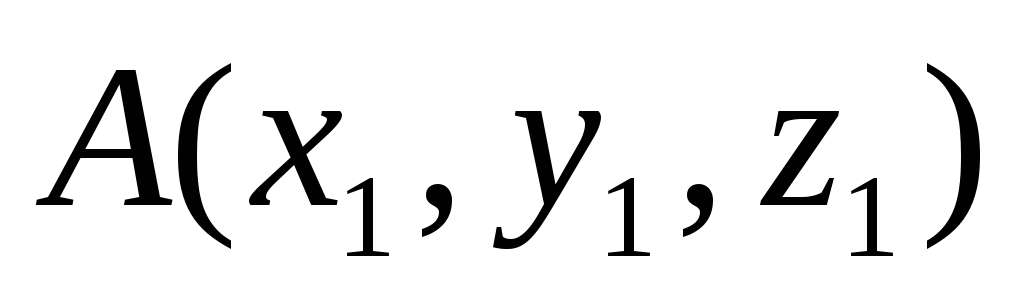 и
и
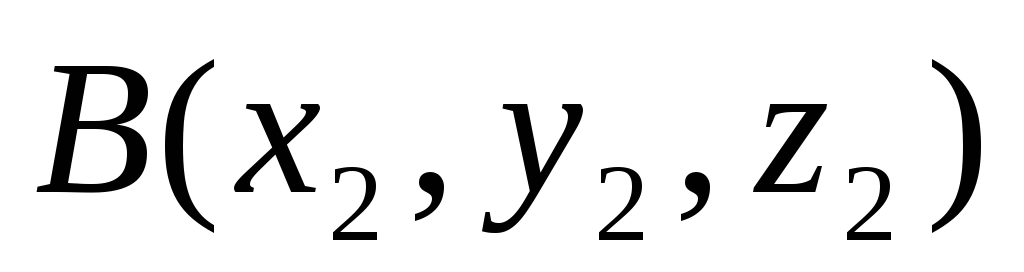 .
Координаты точки D(x, y, z),
делящей отрезок АВ в отношении
AD : DB = λ,
определяются по формулам
.
Координаты точки D(x, y, z),
делящей отрезок АВ в отношении
AD : DB = λ,
определяются по формулам
![]() ,
,
![]() ,
,
![]() .
.
Координаты середины отрезка (т.е. точки С(x, y, z), делящей отрезок АВ в отношении AС : СB = λ = 1) находятся по формулам
![]() ,
,
![]() ,
,
![]() .
.
Пример 2. Найти точку D(x, y, z), делящую отрезок АВ в отношении AD : DB = 1,5, если даны координаты точек A(-2, 1, 4) и B(3, 6, -1).
Решение. Находим
![]() ,
,
![]() ,
,
![]() .
.
Ответ: D(1, 4, 1).
Векторная алгебра
2.2. Векторы
-
Понятие вектора. Различают скалярные величины (такие, как масса, температура, плотность) и векторные величины (сила, скорость, ускорение и т.п.). Скалярные величины охарактеризованы одним числом, выражающим отношение этой величины к единице измерения. Для векторной величины одного числа недостаточно: они обладают еще и направленностью. Для выражения таких величин служат геометрические векторы.
Геометрическим
вектором называется направленный
отрезок.
Векторы обозначаются либо
![]() (точка А
–
начало вектора, точка В
– конец
вектора), либо
(точка А
–
начало вектора, точка В
– конец
вектора), либо
![]() .
Длина отрезка АВ
называется
модулем
вектора
.
Длина отрезка АВ
называется
модулем
вектора
![]() и
обозначается
и
обозначается
![]() (или
(или
![]() ).
).
Нулевым вектором называется вектор, у которого начало и конец совпадают. Коллинеарными векторами называются векторы, лежащие на одной прямой или на параллельных прямых. Векторы называются равными, если они коллинеарны, имеют одинаковые модули и одинаковые направления.
В геометрии не различают равных векторов, получающихся друг из друга параллельным переносом. В этом смысле векторы называют свободными.
-
Произведение вектора на число. Произведением вектора
 на действительное
число
на действительное
число
 называется вектор
называется вектор
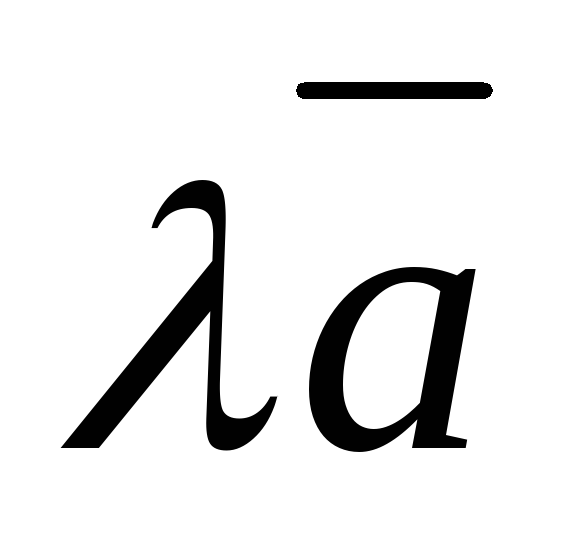 ,
удовлетворяющий
трем условиям: 1) модуль вектора
,
удовлетворяющий
трем условиям: 1) модуль вектора
 равен
равен
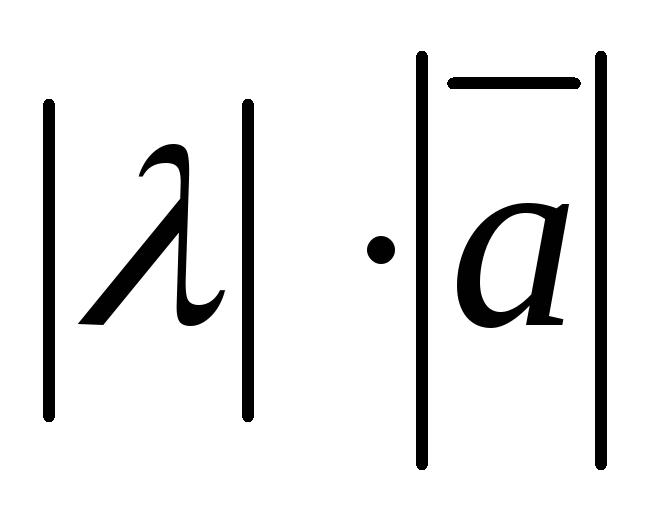 ;
2) вектор
;
2) вектор
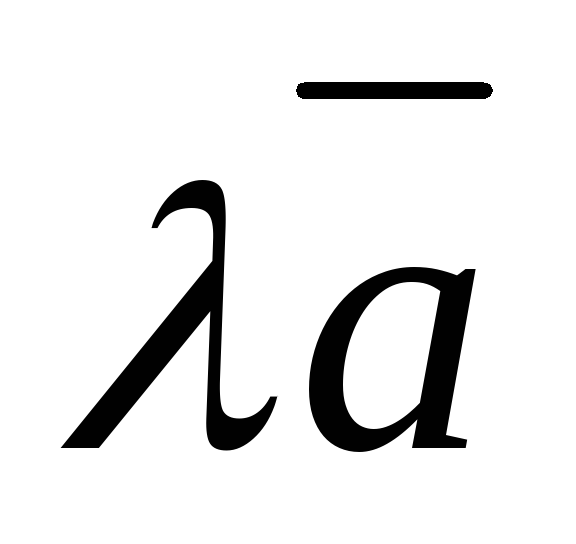 коллинеарен
вектору
коллинеарен
вектору
 ;
3)
;
3)
 и
и
 направлены
одинаково, если
направлены
одинаково, если
 и противоположно, если
и противоположно, если
 (если
(если
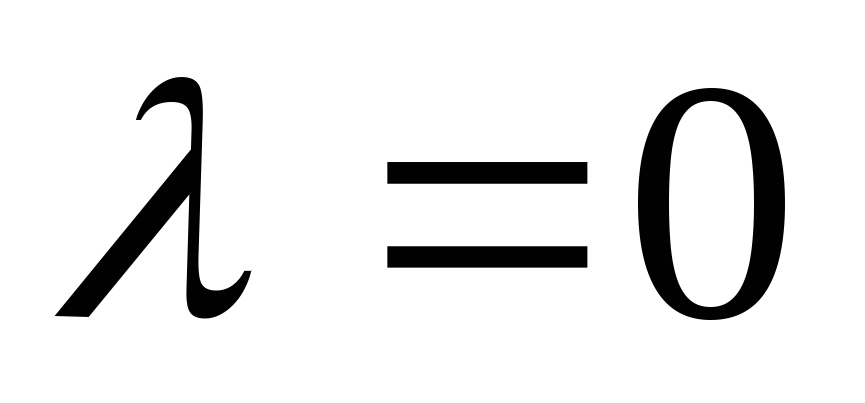 ,
то
,
то
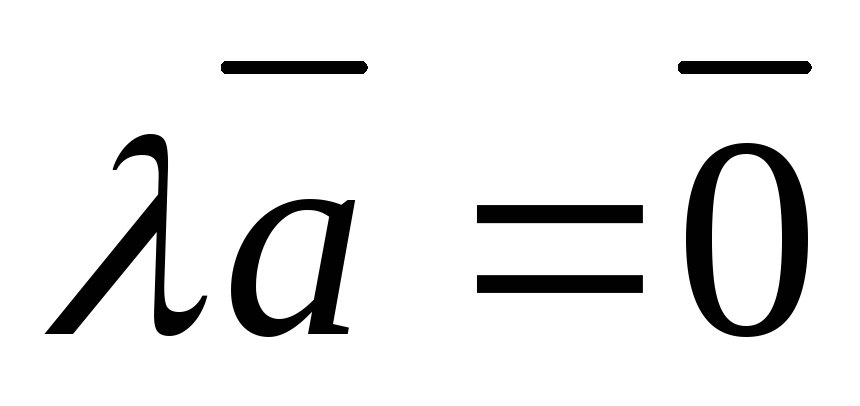 ,
т.е. представляет собой нулевой вектор).
,
т.е. представляет собой нулевой вектор).
Вектор
![]() или
или
![]() называется противоположным
вектором по отношению к вектору
называется противоположным
вектором по отношению к вектору
![]() .
.
-
Сумма векторов. Суммой векторов
 и
и
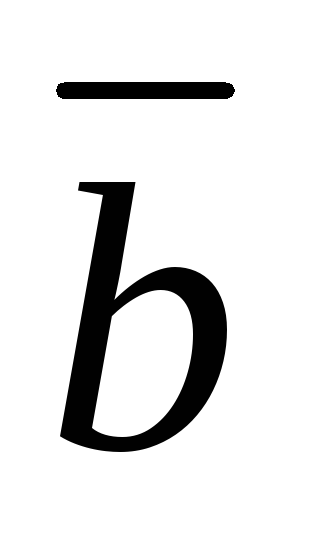 называется вектор
называется вектор
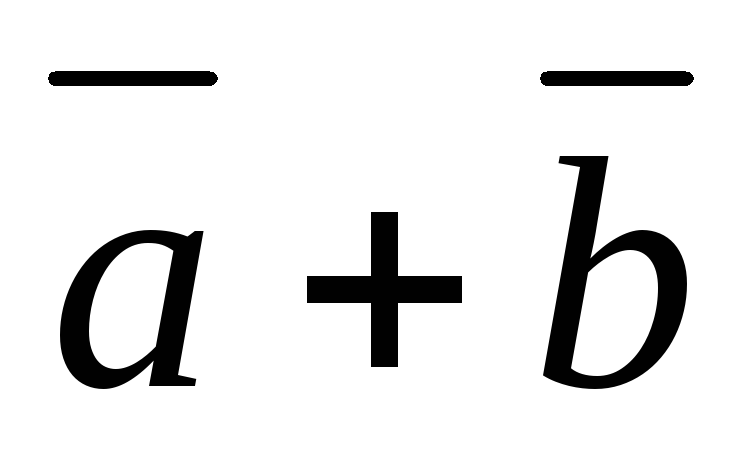 ,
получаемый
либо по правилу
параллелограмма
(рис. 24,
а),
либо
по правилу
треугольника
(рис. 24,
б).
При
этом подразумевается, что векторы
,
получаемый
либо по правилу
параллелограмма
(рис. 24,
а),
либо
по правилу
треугольника
(рис. 24,
б).
При
этом подразумевается, что векторы
 и
и
 предварительно параллельным переносом
должны
занять положение, показанное на рисунках.
предварительно параллельным переносом
должны
занять положение, показанное на рисунках.

Рис. 24.
Сумму
произвольного числа векторов
![]() можно построить по следующему
правилу: приложим вектор
можно построить по следующему
правилу: приложим вектор
![]() к концу вектора
к концу вектора
![]() ,
вектор
,
вектор
![]() – к концу вектора
– к концу вектора
![]() и
т.д.; тогда сумма n
векторов
будет представлять собой вектор, идущий
из начала вектора
и
т.д.; тогда сумма n
векторов
будет представлять собой вектор, идущий
из начала вектора
![]() в
конец вектора
в
конец вектора
![]() ("правило
многоугольника"
или
"правило
замыкающей").
("правило
многоугольника"
или
"правило
замыкающей").
Операция
сложения векторов обладает свойствами
коммутативности
![]() и ассоциативности
и ассоциативности
![]() .
Кроме того, для любого
вектора
.
Кроме того, для любого
вектора
![]() ,
,
![]() ,
также
,
также
![]() и
и
![]() .
.
-
Р
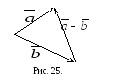 азность
векторов.
Разностью
векторов
азность
векторов.
Разностью
векторов
 и
и
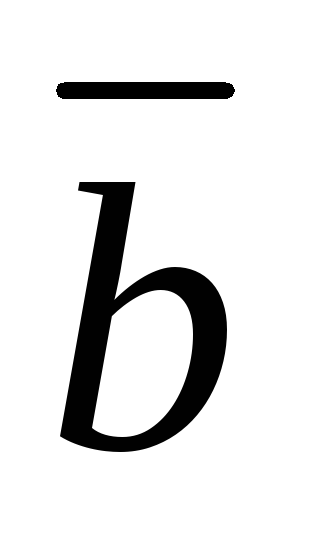 называется
такой вектор
называется
такой вектор
 ,
для которого
,
для которого
 (см.
рис. 25, где векторы
(см.
рис. 25, где векторы
 и
и
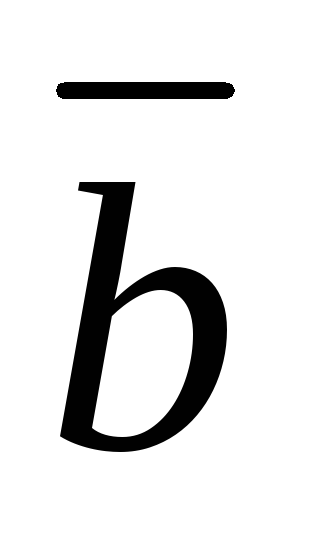 приведены
к общему началу).
приведены
к общему началу).
Можно
рассматривать разность векторов
![]() и
и
![]() как
сумму вектора
как
сумму вектора
![]() и
вектора
и
вектора
![]() ,
противоположного
вектору
,
противоположного
вектору
![]() :
:
![]() .
.
-
Проекция вектора на ось. Углом
 между
осью l
(направленной прямой) и вектором
между
осью l
(направленной прямой) и вектором
 называется
угол кратчайшего поворота оси до
совмещения ее направления с направлением
вектора (аналогично определяется угол
между двумя векторами).
называется
угол кратчайшего поворота оси до
совмещения ее направления с направлением
вектора (аналогично определяется угол
между двумя векторами).
Проекция
вектора
![]() на
ось находится по формуле
на
ось находится по формуле
![]()
(в случае
тупого угла
![]() между
вектором и осью проекция оказывается
отрицательной).
между
вектором и осью проекция оказывается
отрицательной).
-
Разложение вектора по базису. Координаты вектора. Обозначим через
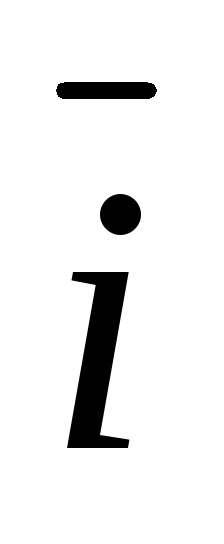 ,
,
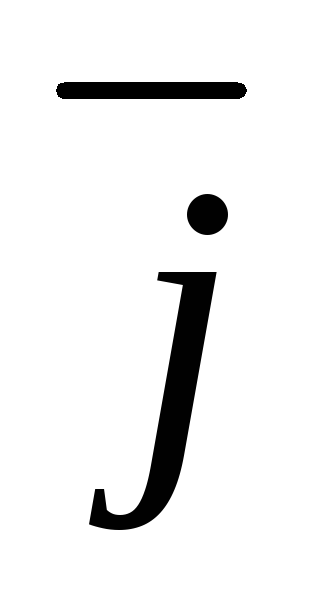 ,
,
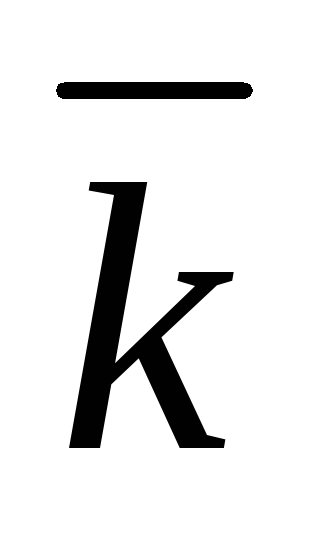 единичные векторы (или орты)
осей
декартовой прямоугольной системы
координат Oxyz.
Любой
вектор
единичные векторы (или орты)
осей
декартовой прямоугольной системы
координат Oxyz.
Любой
вектор
 пространства
единственным образом представляется
в виде
такой линейной
комбинации векторов
пространства
единственным образом представляется
в виде
такой линейной
комбинации векторов
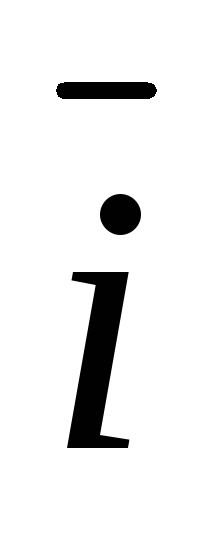 ,
,
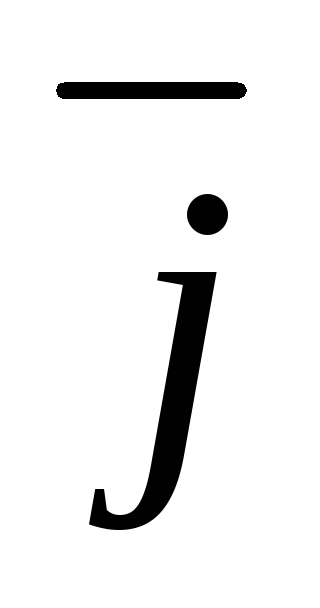 ,
,
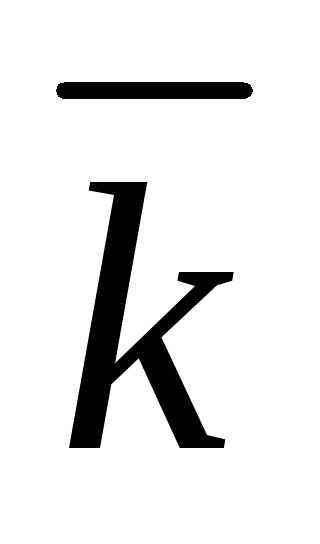 :
:
![]() . (*)
. (*)
Наряду с (*) используется и такая запись:
![]() .
.
Тройку
векторов
![]() ,
,
![]() ,
,
![]() называют
координатным
базисом пространства,
а
представление (*) – разложением
вектора
называют
координатным
базисом пространства,
а
представление (*) – разложением
вектора
![]() по базису.
по базису.
Числа
X,
Y,
Z
–
коэффициенты
этого разложения – называются координатами
вектора
![]() ;
они
определяются вектором
;
они
определяются вектором
![]() однозначно,
а именно, они представляют
собой проекции вектора на оси координат.
однозначно,
а именно, они представляют
собой проекции вектора на оси координат.
Замечание.
Разложение
векторов можно производить не только
по ортогональному
базису
![]() ,
,
![]() ,
,
![]() ,
но и по любым трем некомпланарным
(т.е.
не лежащим в одной плоскости)
векторам (если вектор лежит на плоскости,
то в качестве базиса можно
взять любую пару неколлинеарных
векторов).
,
но и по любым трем некомпланарным
(т.е.
не лежащим в одной плоскости)
векторам (если вектор лежит на плоскости,
то в качестве базиса можно
взять любую пару неколлинеарных
векторов).
-
Определение координат вектора по координатам его начала и конца. Если даны начало вектора
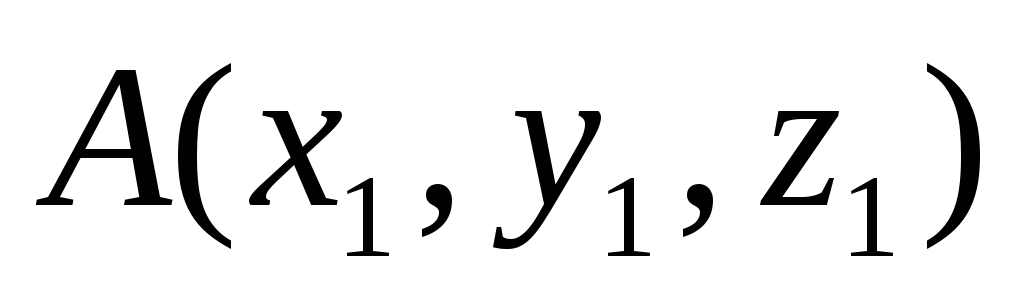 и его
конец
и его
конец
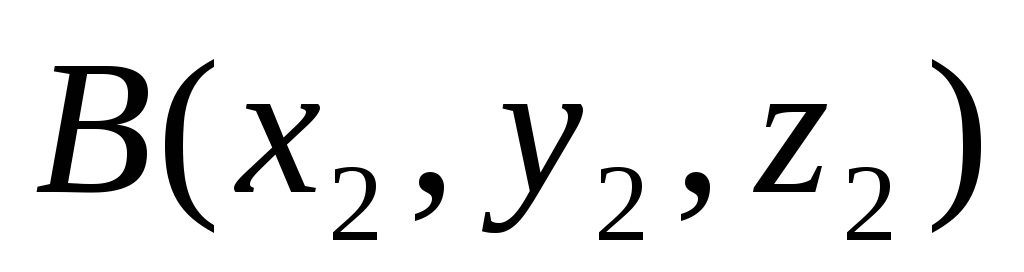 ,
то имеем
,
то имеем
![]() или
или
![]() .
.
В частном
случае, когда начало вектора
![]() находится
в начале координат, имеем
находится
в начале координат, имеем
![]() ,
т.е. в этом случае координаты вектора
совпадают
с координатами конца вектора (отметим,
что вектор
,
т.е. в этом случае координаты вектора
совпадают
с координатами конца вектора (отметим,
что вектор
![]() называют
радиусом-вектором
точки В).
называют
радиусом-вектором
точки В).
Модуль
вектора
![]() (как и длина отрезка АВ)
находится
по формуле
(как и длина отрезка АВ)
находится
по формуле
![]() .
.
В
частности, модуль вектора
![]() с
началом в точке О
равен
с
началом в точке О
равен
![]() .
.
Пример 1.
Пусть
начало вектора расположено в точке
A(-3, 1, 5),
а конец
– в точке B(-2, 0, 4).
Тогда
вектор
![]() или же
или же
![]() ,
а модуль этого вектора
,
а модуль этого вектора
![]() ;
радиус-вектор точки В
равен
;
радиус-вектор точки В
равен
![]() ,
а
,
а
![]() .
.
-
Координаты суммы векторов равны суммам одноименных координат слагаемых: если
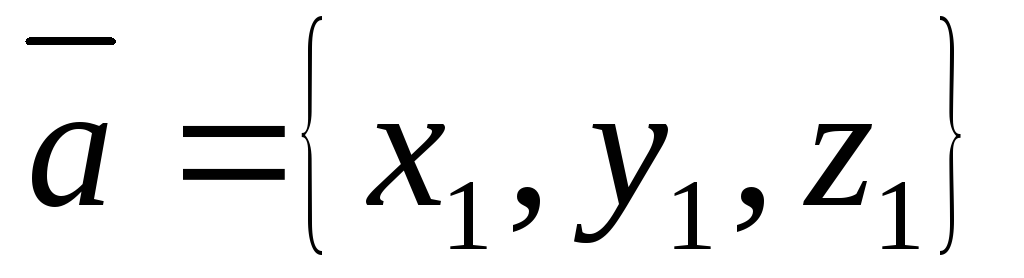 ,
,
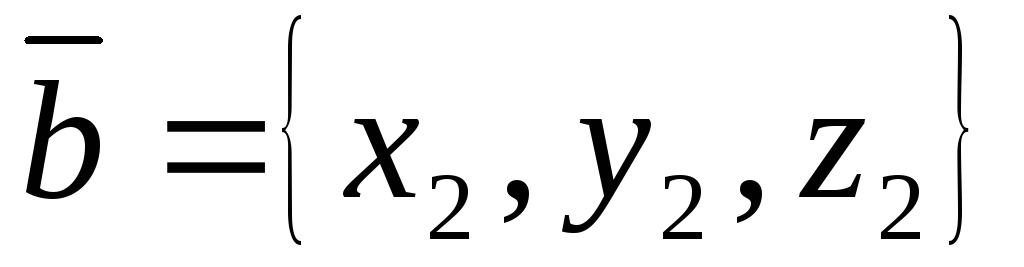 ,
то
,
то
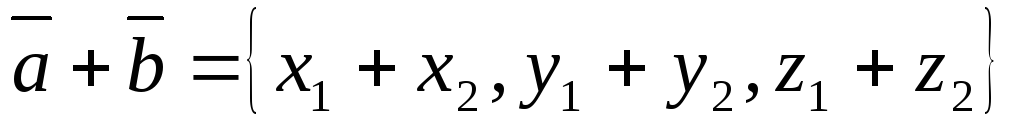 .
.
Аналогично
![]() ;
кроме
того, координаты вектора
;
кроме
того, координаты вектора
![]() равны произведениям координат вектора
равны произведениям координат вектора
![]() на число
на число
![]() :
:
![]() .
.
Пример 2.
Найти
координаты вектора
![]() ,
если
,
если
![]() ,
,
![]() .
.
Решение.
Находим
![]() ,
,
![]() ,
поэтому
,
поэтому
![]() .
.
