4. Элементы потока

Рассмотрим в качестве примера поток жидкости в круглой трубе, рис. 4.1.а (вид сбоку). На этом рисунке горизонтальными линиями изображены линии тока; проведём плоскость П перпендикулярно направлению струек. Тогда на плоскости получится сечение потока (заштриховано) рис. 4.1.б, которое носит название живого сечения потока. Сечение потока, во всех точках которого линии тока, пересекающие эту поверхность, перпендикулярны к ней, называется живым сечением потока.

На рис. 4.2 изображены живые сечения: а) напорной трубы; б) трубы, работающей неполным сечением; в) квадратной напорной трубы; г) трапецеидального канала; д) прямо-угольного канала. Площадь сечения обычно обозначается буквой S. Если бы струйки в потоке не были параллельны, то живое сечение представляло бы часть криволинейной поверхности. В гидравлических расчётах применяют также смоченный периметр и гидравлический радиус.

а)	б)	в)	г)	д)

Рис.4.2

Смоченный периметр представляет собой длину линии, по которой жидкость в живом сечении соприкасается с твёрдыми поверхностями, ограничивающими поток.

В напорных потоках длина смоченного периметра  равна длине всего периметра живого сечения, а в безнапорных потоках – части полного периметра, рис.4.2

Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру в этом сечении. Обычно гидравлический радиус обозначается буквой R и определяется так

. (4.1)

5. Уравнение неразрывности для потока

Поток конечных размеров часто представляется как совокупность элементарных струек. Так как скорость течения в разных струйках в общем случае неодинаковая, то скорость в различных точках живого (поперечного) сечения будет иметь разные значения. Закон распределения скорости характеризуется эпюрой скорости, рис 5.1. Очевидно, что расход потока в каждом сечении равен сумме расходов всех элементарных струек, т. е.

,

что можно точнее записать, проинтегрировав расходы струек по всему живому сечению потока

. (5.1)

Для потока, если нет присоединений и ответвлений расхода,

, (5.2)

т.е. по длине потока величина расхода остаётся постоянной, какое бы сечение не рассматривается.

Д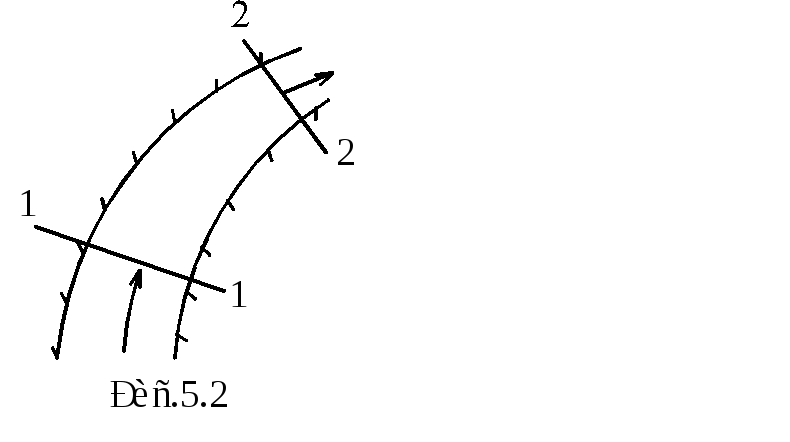ля понимания уравнения (5.2) достаточно элементарных представлений, а именно если через сечение 1-1, рис.5.2 каждую единицу времени подавать жидкость в определенном объёме (т.е. подавать определённый расход), то через произвольно выбранное сечение 2-2 (а значит, и вообще через любое сечение) должно проходить (при установившемся движении) точно такое же количество жидкости. В противном случае жидкость где-то между этими сечениями будет или исчезать или появляться, что в соответствии со здравым смыслом невозможно. Таким образом, необходимо подчеркнуть это ещё раз, расход жидкости в любом сечении имеет одно и то же значение. Учитывая исключительно важное значение понятия расхода в гидравлических расчётах приведём его определение ещё раз.

Расходом называется объём жидкости, проходящей через поперечное сечение потока за единицу времени.

Это определение относится к объему, в то время как очевидно, что всегда неизменна вдоль потока масса жидкости, протекающая через сечение за единицу времени так называемый массовый расход

и только в том случае, если плотность жидкости или газа постоянна в каждом сечении, из последнего равенства следует

.

Равенство тем не менее справедливо в большинстве гидравлических явлений, за исключении течений газа со скоростями, сравнимыми со скоростью звука.

Непосредственно из определения следует, что для нахождения расхода в опытах необходимо поток направить в мерную ёмкость, набрать некоторый объём W за время t, а затем найти расход Q с помощью зависимости

.

Такой способ называется объёмным способом определения расхода и очень распространён.