2. Поняття інфімума та супремума множини

Визначення 6. Множина називається обмеженою знизу (зверху), якщо існує така стала (), що для виконується: (). В цьому випадку () називається нижньою (верхньою) межею множини .

Приклад. - сегмент. - нижня межа , бо всі елементи будуть більшими за 0. Крім того нижньою межею також можуть бути числа: , , . Взагалі будь-яке число, меньше чи рівне 3, є нижньою межею , множина - обмежена знизу. Будь-яке число, що більше або дорівнює 9, буде верхньою межею , тому - множина, обмежена зверху.

З розглянутого прикладу зрозуміло: якщо деяка множина обмежена знизу (чи зверху), вона має безліч нижніх (чи верхніх) меж.

Приклад. Множина натуральних чисел обмежена знизу, бо всі натуральні числа більші за 0, тобто 0 – це одна з нижніх меж, але - не обмежена зверху.

Визначення 7. Множина називається обмеженою, якщо вона обмежена знизу і зверху, тобто існує така стала , що для виконується: .

Таким чином, - обмежена множина, а - необмежена множина.

Визначення 8. Число називається точною нижньою межею, чи інфімумом множини і позначається , якщо виконуються наступні умови:

1. - нижня межа ;

2. Для 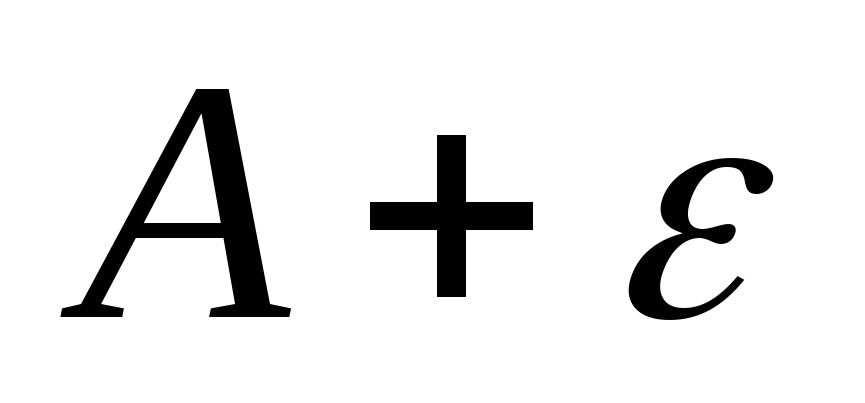вже не буде нижньою межею для 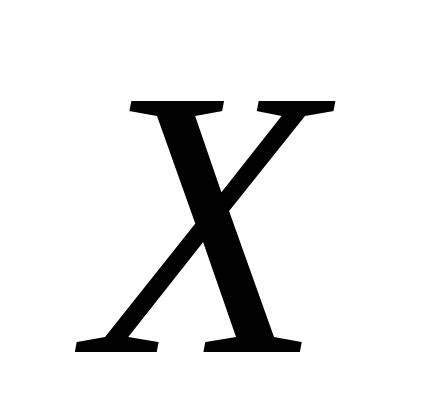, тобто знайдеться такий елемент , що .

Таким чином, точна нижня межа – це найбільша з усіх нижніх меж множини, вона визначається однозначно. Так для попередніх прикладів, коли , то , а .

Визначення 9. Число називається точною верхньою межею, чи супремумом множини і позначається , якщо виконуються наступні умови:

1. - верхня межа ;

2. Для вже не буде верхньою межею для , тобто знайдеться такий елемент , що .

Таким чином, точна верхня межа – це найменьша з усіх верхніх меж множини, вона визначається однозначно. Для попередніх прикладів, коли , то , а не існує.

Якщо множина обмежена зверху (знизу), в неї обов’язково існує точна верхня (нижня) межа.

3. Лема про вкладені відрізки

Аксіома повноти. Якщо , і для , виконується нерівність

,

то існує така стала , що для виконується: .

Будемо казати, що відрізок вкладений у відрізок , якщо (чи інакше: ). Позначимо .

Лема (про вкладені відрізки). Будь-яка послідовність вкладених відрізків має хоча б одну спільну точку. Якщо для існує відрізок такий, що його довжина меньша за , то така точка єдина.

Зауваження. Не будь-яка послідовність вкладених інтервалів чи напівінтервалів має спільну точку.

Приклад. Нехай , де . Така сукупність спільної точки не має.

4. Поняття покриття множини. Лема Бореля

Нехай – деяке сімейство (сукупність) множин.

Сукупність називається покриттям множини А, якщо кожний елемент А належить хоча б одному з , тобто .

Лема (Бореля). З будь-якої нескінченної сукупності інтервалів, що покривають сегмент , можна виділити скінченну сукупність інтервалів, яка також покриває .

Якщо покриття таке, що його елементи попарно не перетинаються (), і всі , те таке покриття називається розбивкою множини А.

Приклад. . Тоді - покриття, але не розбивка, - розбивка і покриття, - не є ні покриттям, ні розбивкою.