Властивості підмножин

1. Для будь-якої множини вона є своєю підмножиною. З використанням введених кванторів ця властивість може бути записано наступним чином:

.

2. якщо , то .

3. якщо , то . Ця властивість є умовою рівності двох множин.

4. якщо , то .

5. .

Необхідно розрізняти відношення включення, тобто відношення «бути підмножиною» (це відношення між множинами) і приналежності (відношення між елементами й множиною). Наведені вище властивості не мають місця для відношення приналежності. Наприклад: . Звідси не випливає, що .

Будь-яка непорожня множина має завжди хоча б 2 підмножини: . Якщо містить елементів, та кількість різних її підмножин - .

Визначення 4. Говорять, що між множинами і встановлена взаємо-однозначна відповідність, якщо кожному елементу множини відповідає один і тільки один елемент множини В, і кожному елементу множини В відповідає один елемент множини А.

Якщо між множинами і може бути встановлена взаємо-однозначна відповідність, то множини мають однакову потужність і називаються рівнопотужними: .

Приклад. Множина десяткових цифр рівнопотужна множині пальців на руках людини, але не рівнопотужна множині пальців на руках і ногах.

Приклад. Множина парних натуральних чисел рівнопотужна множині всіх натуральних чисел.

Операції над множинами

Об'єднання множин – це множина

.

Визначається однозначно.

Переріз множин – це множина

.

Для будь-яких множин маємо:

.

Дві множини називаються неперетинними, якщо , і перетинними інакше.

Абсолютне доповнення (або просте доповнення) множини А - це

.

Відносне доповнення множини В до множини А (або різниця А-В) – це

.

Симетрична різниця А і В: .

Властивості:

;

;

.

Властивості операцій над множинами

Теорема 1. Нехай - універсальна множина, тобто множина, яка для конкретної розглянутої задачі включає всі інші множини як підмножини. Для мають місце рівності:

1. Ідемпотентність:

; ;

2. Комутативність:

, ;

3. Асоціативність:

, ;

4. Дистрибутивність:

, ;

5. , ;

6. , .

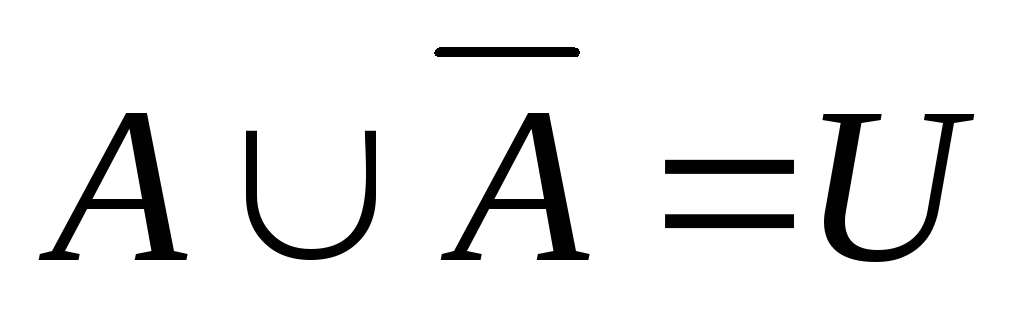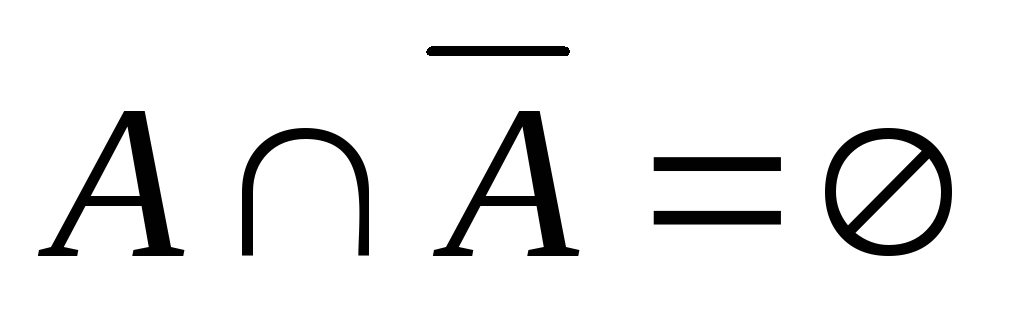Властивості множин у теоремі 1 записуються парами. Рівність теорії множин, яка виходить із іншої рівності заміною всіх операцій на , на , на , на , називається двоїстою до вхідної.

Принцип двоїстості: Якщо в теорії множин можна показати справедливість якогось твердження, то двоїсте твердження також буде мати місце.

З теореми 1 випливає, що об'єднання й переріз множин А,В,С можна записувати без дужок: , .

Методом математичної індукції можна довести, що об'єднання й переріз будь-якого числа множин можна записувати без дужок, тобто

, - загальні асоціативні закони.

Мають місце загальні комутативні й дистрибутивні закони:

, де - будь-яка перестановка чисел ;

.

Теорема 2. Нехай - універсальна множина. Для мають місце рівності ():

1. Якщо для всіх А . Якщо для всіх А .

2. Якщо і , то .

3. ;

4. , ;

5. Закони поглинання:

, ;

6. Закони де-Моргана:

, .

Теорема 3. Твердження , , еквівалентні для будь-яких множин А и В.