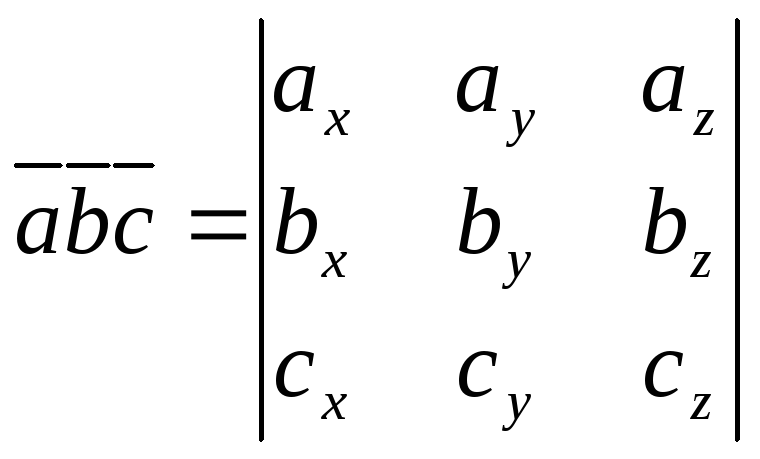- •Определители
- •Свойства определителя:
- •Обратная матрица
- •Правило вычисления обратной матрицы:
- •Решение систем линейных алгебраических уравнений
- •Решение однородных систем
- •Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Сумма векторов
- •Разность векторов
- •Умножение вектора на число
- •Проекция вектора на ось
- •Свойства проекций:
- •Линейные операции над векторами, заданными в координатной форме:
- •Представление вектора в декартовой системе координат
- •Направляющие косинусы вектора
- •Координаты точки, радиус-вектор точки
- •Деление отрезка в данном отношении
- •Произведения векторов Скалярное произведение векторов и его свойства
- •Свойства скалярного произведения
- •Выражение скалярного произведения через координаты сомножителей
- •Некоторые приложения скалярного произведения
- •Векторное произведение и его свойства
- •Свойства векторного произведения
- •Выражение векторного произведения через координаты сомножителей
- •Приложения векторного произведения
- •Смешанное произведение векторов
- •Свойства смешанного произведения
- •Выражение смешанного произведения через координаты сомножителей
- •Приложения смешанного произведения
- •Прямая на плоскости Линия на плоскости
- •Общее уравнение прямой линии на плоскости
- •Прямая, проходящая через точку, перпендикулярно данному вектору
- •Прямая, проходящая через точку, параллельно данному вектору
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой в отрезках
- •Уравнение прямой с угловым коэффициентом
- •Прямая, проходящая через точку, в данном направлении
- •Угол между прямыми
- •Точка пересечения прямых
- •Расстояние от точки до прямой
- •Проекция точки на прямую
- •Плоскость Общее уравнение плоскости
- •Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •Особенности в расположении плоскостей
- •Уравнение плоскости, проходящей через данную точку, параллельно двум неколлинеарным векторам
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •Основные задачи
- •Прямая линия в пространстве Общее уравнение прямой
- •Уравнение прямой, проходящей через заданную точку, перпендикулярно данной плоскости
- •Перевод уравнения прямой из канонического вида в параметрический
- •Перевод уравнения прямой из общего вида в канонический
- •Угол между прямыми в пространстве
- •Взаимное расположение прямых в пространстве
- •Угол между прямой и плоскостью
- •Пересечение прямой и плоскости
- •Кривые второго порядка
- •Гипербола
- •Парабола
Свойства векторного произведения
-
.При перестановке сомножителей векторное произведение меняет знак, т. е.
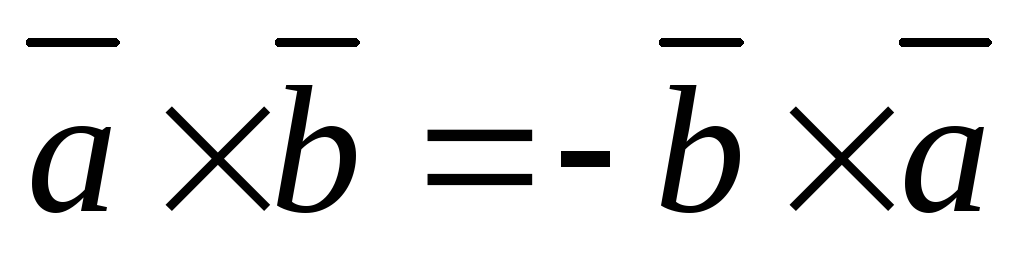 .
.
-
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е.
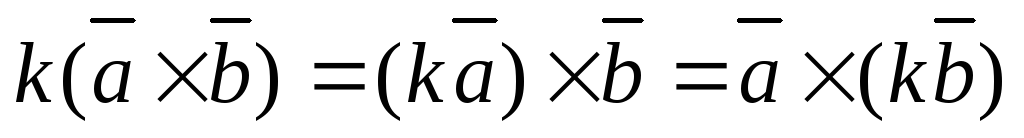 .
. -
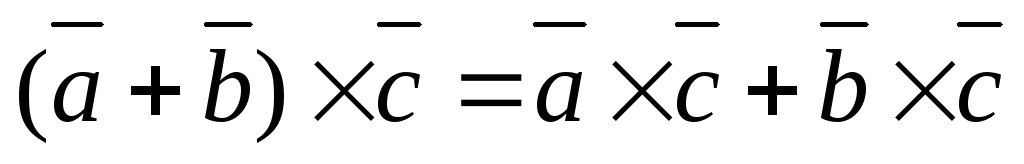 .
. -
Если два ненулевых вектора коллинеарны, то их векторное произведение равно нулю, и наоборот, из равенства нулю векторного произведения следует коллинеарность векторов.
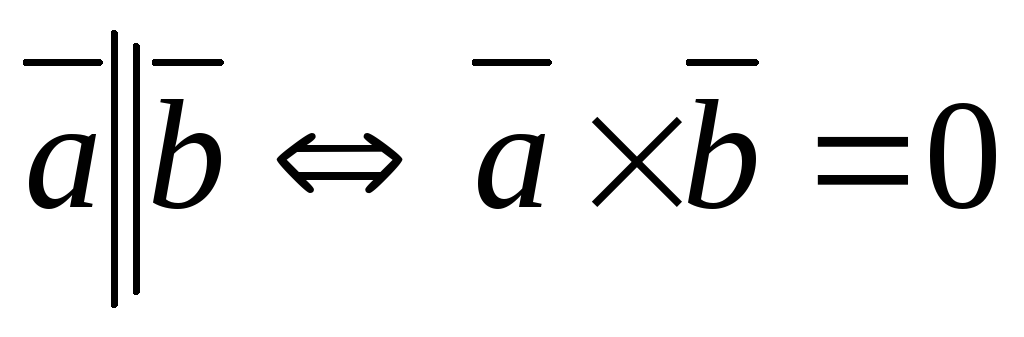
-
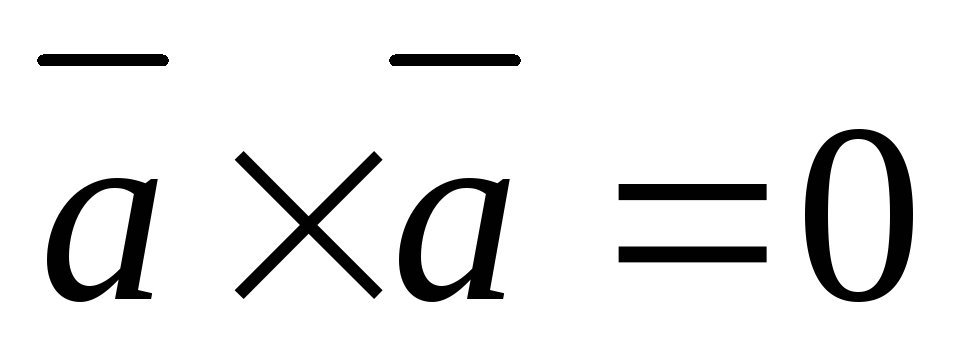
Выражение векторного произведения через координаты сомножителей
Пусть
даны два вектора
![]() и
и
![]() .
.
Найдем их векторное произведение, перемножая их как многочлены, используя свойства векторного произведения:
![]() +
+
![]()
![]()
Полученную формулу можно записать еще короче
-
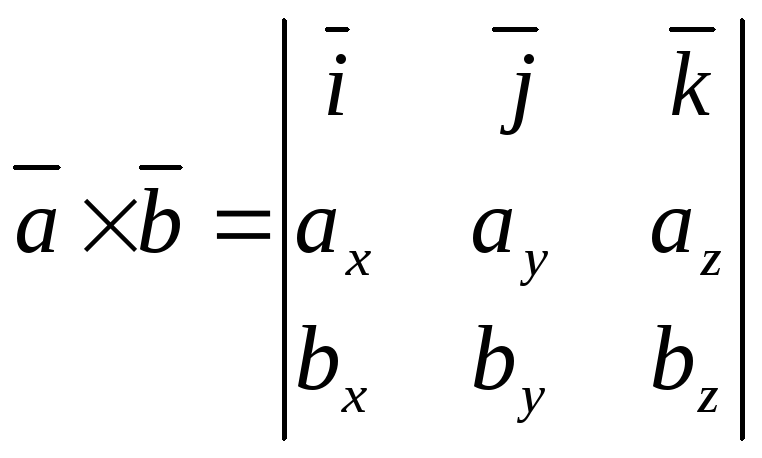 =
=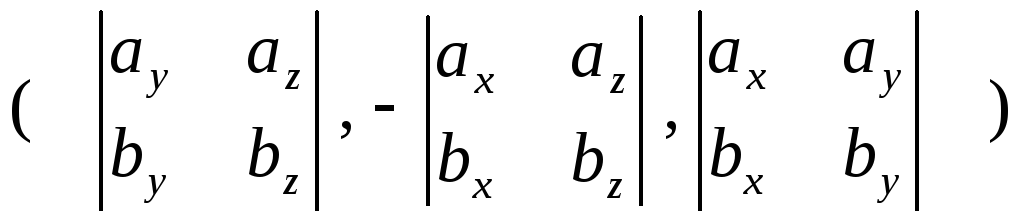
Приложения векторного произведения
Площадь параллелограмма и треугольника
Площадь
параллелограмма равна модулю векторного
произведения двух его смежных сторон:
![]() ,
,
Площадь
треугольника, построенного на двух
сторонах равна половине модуля векторного
произведения:
![]()
Условие коллинеарности векторов
Если
![]() то
то
![]() и наоборот, т.е.
и наоборот, т.е.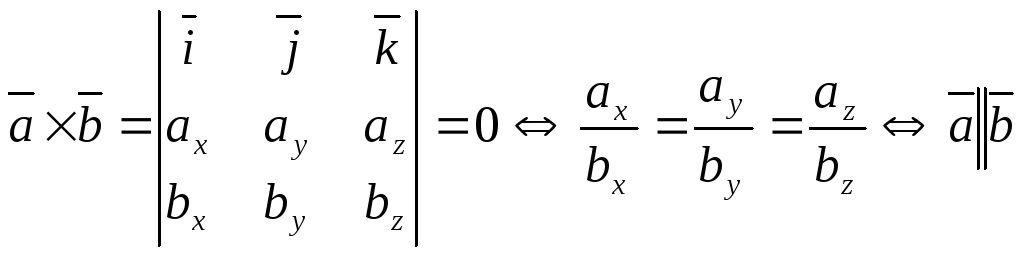
Смешанное произведение векторов
Рассмотрим
произведение векторов
![]() и
и
![]() ,
составленное следующим образом:
,
составленное следующим образом:![]() .
Здесь первые два вектора перемножаются
векторно, а их результат скалярно на
третий вектор. Такое произведение
называется векторно-скалярным, или
смешанным, произведением трех векторов.
Смешанное произведение представляет
собой некоторое число. Обозначается
смешанное произведение:
.
Здесь первые два вектора перемножаются
векторно, а их результат скалярно на
третий вектор. Такое произведение
называется векторно-скалярным, или
смешанным, произведением трех векторов.
Смешанное произведение представляет
собой некоторое число. Обозначается
смешанное произведение:
![]()
С
Свойства смешанного произведения
1.
Смешанное произведение не меняется при
циклической перестановке его
сомножителей, т. е.![]() .
.
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2.
Смешанное произведение меняет свой
знак при перемене мест любых двух
векторов-сомножителей, т. е.![]() ,
,
![]() .
.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении меняющей у произведения знак.
3.Смешанное
произведение ненулевых векторов
![]() и
и
![]() равно
нулю тогда и только тогда, когда они
компланарны.
равно
нулю тогда и только тогда, когда они
компланарны.
Выражение смешанного произведения через координаты сомножителей
Пусть векторы заданы своими координатами:
![]() ,
,
![]() ,
,![]()
![]() .
Найдем их смешанное произведение,
используя формулы для выражения
векторного и скалярного произведений:
.
Найдем их смешанное произведение,
используя формулы для выражения
векторного и скалярного произведений:
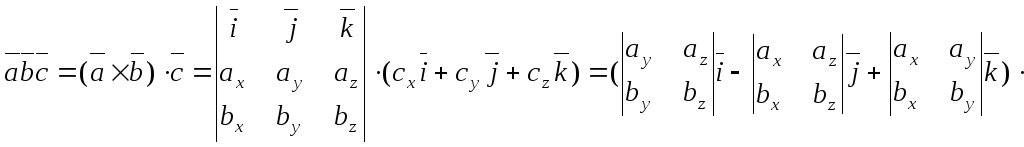
![]() .
.
Полученную формулу можно записать короче:
|
|
так как правая часть равенства представляет собой разложение определителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Приложения смешанного произведения
-
Определение взаимной ориентации векторов в пространстве. Если
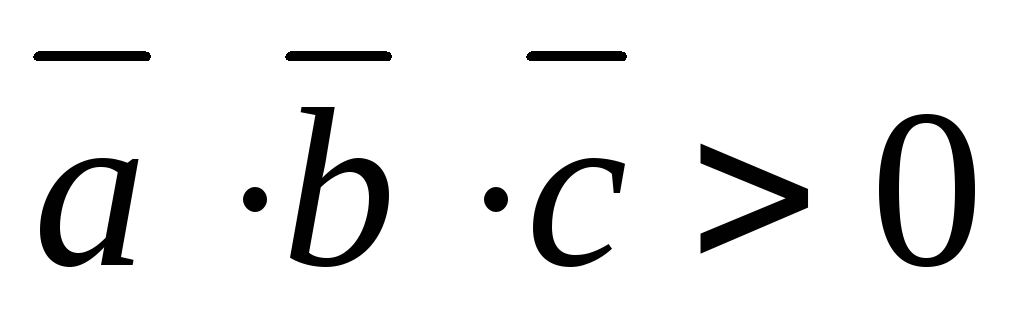 ,то тройка
,то тройка
 —
правая; если
—
правая; если
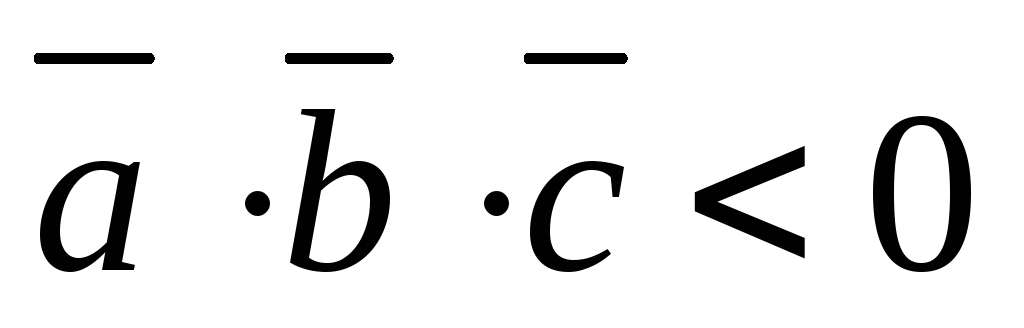 , то
, то
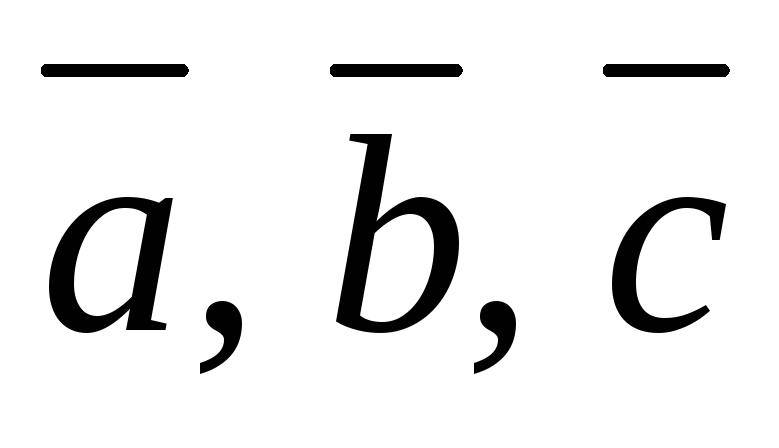 -
левая тройка.
-
левая тройка. -
Установление компланарности векторов. Векторы
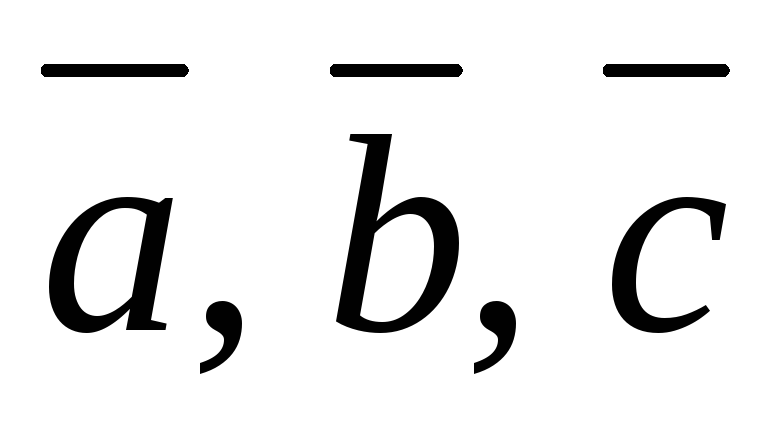 компланарны тогда и только тогда, когда
их смешанное произведение равно нулю
компланарны тогда и только тогда, когда
их смешанное произведение равно нулю
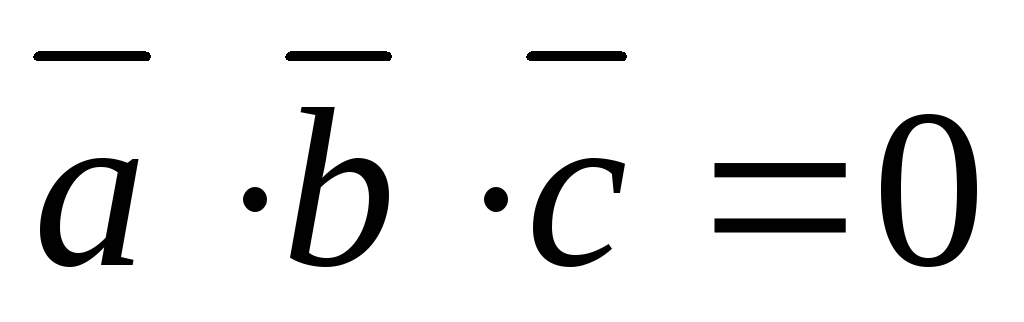 .
.
-
Объем параллелепипеда и треугольной пирамиды.
Модуль
смешанного произведения численно равен
объему параллелепипеда, построенного
на векторах
![]() ,
как на сторонах, т.е.
,
как на сторонах, т.е.
![]()
![]() -
объем параллелепипеда;
-
объем параллелепипеда;
![]() -
объем пирамиды, построенной на векторах
-
объем пирамиды, построенной на векторах
![]()
Пример:
По
координатам вершин пирамиды
![]() найти:
найти:
1)
косинус угола между ребрами
![]() и
и
![]() ;
;
2)
площадь треугольника
![]() -
основания пирамиды;
-
основания пирамиды;
3)
объем пирамиды
![]() ;
;
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Решение:
1)
Найдем координаты векторов
![]() и
и
![]() ;
;
![]() ,
,
![]()
Косинус
угола между векторами находится по
формуле
![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
Ответ:
![]() .
.
2)
площадь треугольника
![]() вычисляется по формуле:
вычисляется по формуле:
![]() ,
,
![]() ,
,
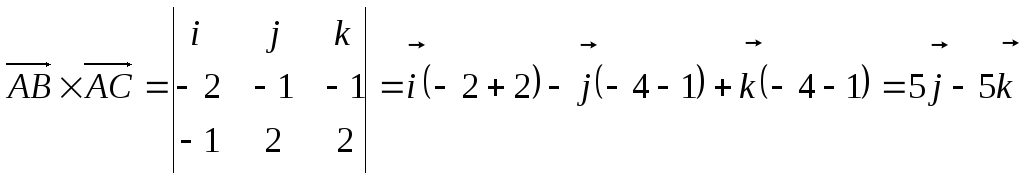 ,
,
![]()
Ответ:
![]() кв.ед.
кв.ед.
3)
Найдем объем пирамиды
![]() :
:
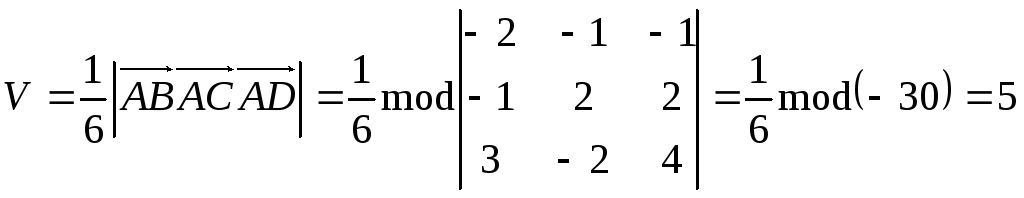 .
.
Ответ:
![]() куб.ед.
куб.ед.