- •Определители
- •Свойства определителя:
- •Обратная матрица
- •Правило вычисления обратной матрицы:
- •Решение систем линейных алгебраических уравнений
- •Решение однородных систем
- •Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Сумма векторов
- •Разность векторов
- •Умножение вектора на число
- •Проекция вектора на ось
- •Свойства проекций:
- •Линейные операции над векторами, заданными в координатной форме:
- •Представление вектора в декартовой системе координат
- •Направляющие косинусы вектора
- •Координаты точки, радиус-вектор точки
- •Деление отрезка в данном отношении
- •Произведения векторов Скалярное произведение векторов и его свойства
- •Свойства скалярного произведения
- •Выражение скалярного произведения через координаты сомножителей
- •Некоторые приложения скалярного произведения
- •Векторное произведение и его свойства
- •Свойства векторного произведения
- •Выражение векторного произведения через координаты сомножителей
- •Приложения векторного произведения
- •Смешанное произведение векторов
- •Свойства смешанного произведения
- •Выражение смешанного произведения через координаты сомножителей
- •Приложения смешанного произведения
- •Прямая на плоскости Линия на плоскости
- •Общее уравнение прямой линии на плоскости
- •Прямая, проходящая через точку, перпендикулярно данному вектору
- •Прямая, проходящая через точку, параллельно данному вектору
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой в отрезках
- •Уравнение прямой с угловым коэффициентом
- •Прямая, проходящая через точку, в данном направлении
- •Угол между прямыми
- •Точка пересечения прямых
- •Расстояние от точки до прямой
- •Проекция точки на прямую
- •Плоскость Общее уравнение плоскости
- •Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •Особенности в расположении плоскостей
- •Уравнение плоскости, проходящей через данную точку, параллельно двум неколлинеарным векторам
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •Основные задачи
- •Прямая линия в пространстве Общее уравнение прямой
- •Уравнение прямой, проходящей через заданную точку, перпендикулярно данной плоскости
- •Перевод уравнения прямой из канонического вида в параметрический
- •Перевод уравнения прямой из общего вида в канонический
- •Угол между прямыми в пространстве
- •Взаимное расположение прямых в пространстве
- •Угол между прямой и плоскостью
- •Пересечение прямой и плоскости
- •Кривые второго порядка
- •Гипербола
- •Парабола
Произведения векторов Скалярное произведение векторов и его свойства
Опр:
Скалярным
произведением
двух ненулевых векторов ![]() и
и ![]() называется число, равное произведению
длин этих векторов на косинус угла между
ними.
называется число, равное произведению
длин этих векторов на косинус угла между
ними.
![]()
где
- угол между векторами
![]() и
и
![]() .
Для скалярного произведения применяются
обозначения:
.
Для скалярного произведения применяются
обозначения: ![]() ,
или
,
или ![]() ,
или (
,
или (![]() ).
).
Формуле
можно придать иной вид. Так как ![]() ,
,
![]() ,
то получаем:
,
то получаем:
![]()
т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого в направлении первого.
Свойства скалярного произведения
-
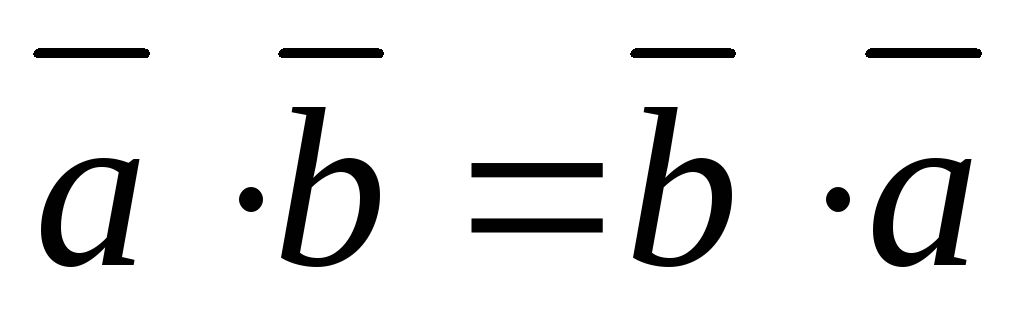
-
(
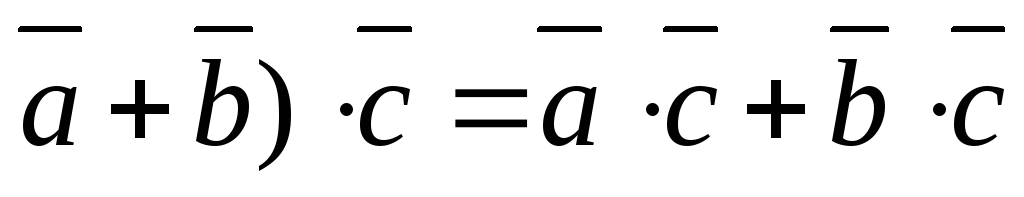
-
(
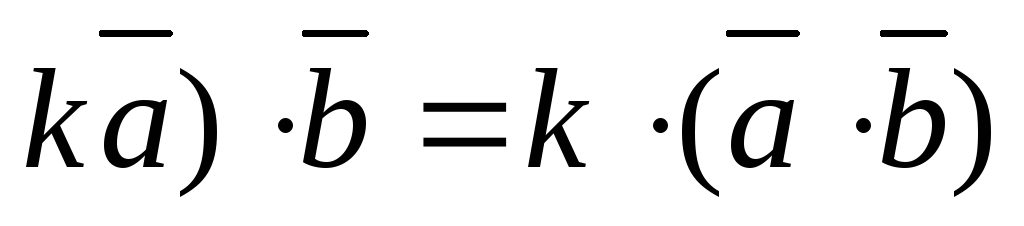

-
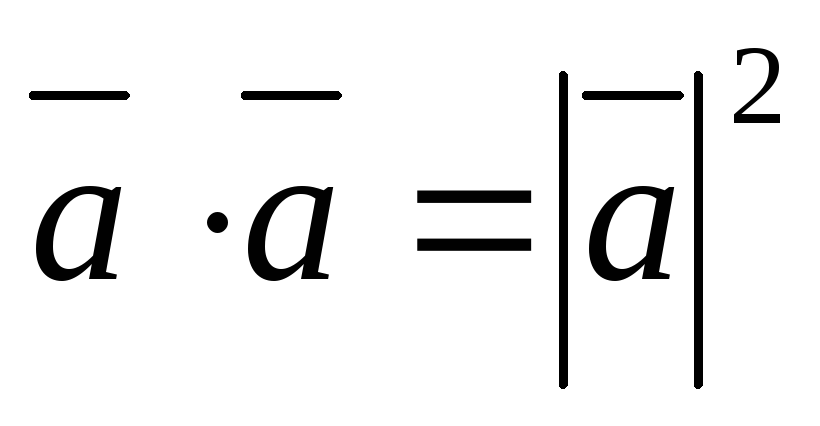 скалярный
квадрат равен квадрату модуля вектора.
скалярный
квадрат равен квадрату модуля вектора.
-
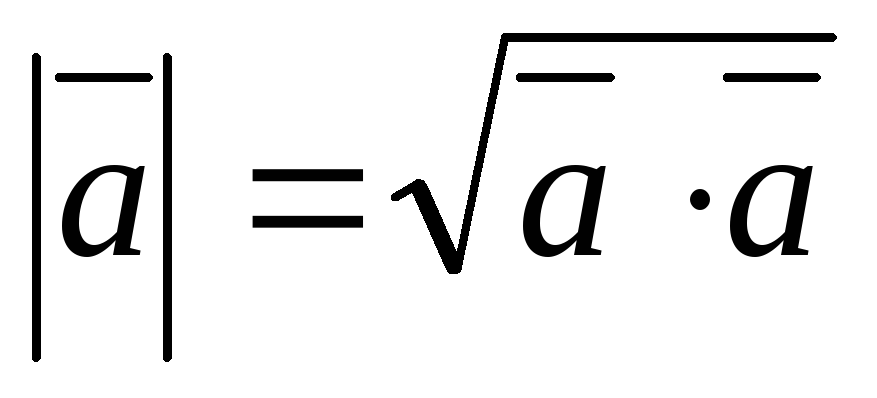 модуль
вектора равен корню из скалярного
квадрата.
модуль
вектора равен корню из скалярного
квадрата. -
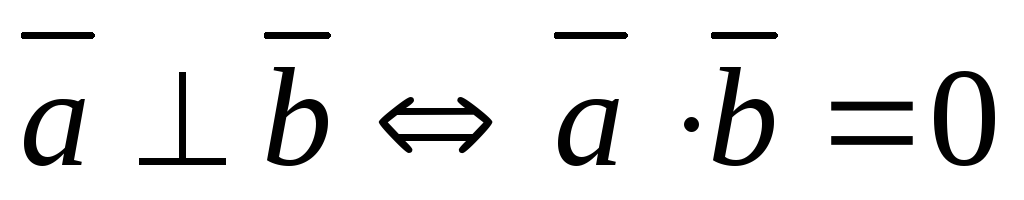 если
ненулевые векторы
если
ненулевые векторы
 и
и
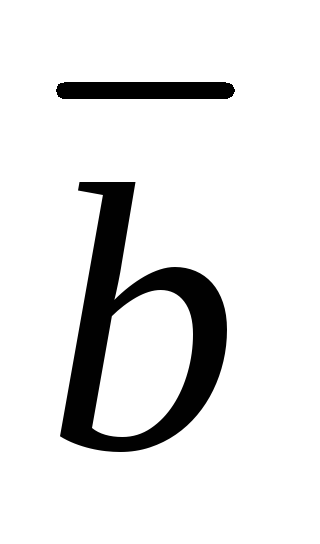 перпендикулярны, то их скалярное
произведение равно нулю, и наоборот,
если скалярное произведение векторов
равно нулю, то векторы перпендикулярны.
перпендикулярны, то их скалярное
произведение равно нулю, и наоборот,
если скалярное произведение векторов
равно нулю, то векторы перпендикулярны.
Выражение скалярного произведения через координаты сомножителей
Пусть
заданы два вектора
![]() и
и
![]() .
Составим таблицу скалярных произведений
орт:
.
Составим таблицу скалярных произведений
орт:
Найдем
скалярное произведение векторов,
перемножая их как многочлены (что законно
в силу свойств линейности скалярного
произведения) и пользуясь таблицей
скалярного произведения орт
![]()
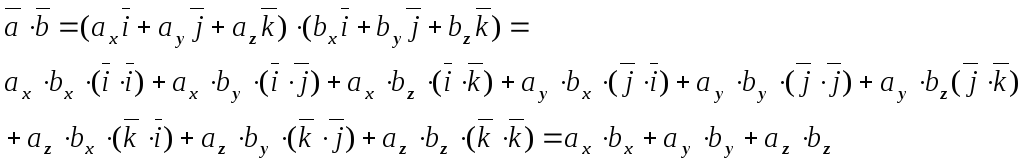
![]()
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
|
|
Пример 1. Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-3;2;2), С(2;5;1), D(3;-2;2), взаимно перпендикулярны.
Решение:
Составим вектора ![]() и
и ![]() ,
лежащие на диагоналях данного
четырехугольника. Имеем:
,
лежащие на диагоналях данного
четырехугольника. Имеем: ![]() =(6;9;-3)
и
=(6;9;-3)
и ![]() =(6;-4;0).
Найдем скалярное произведение этих
векторов:
=(6;-4;0).
Найдем скалярное произведение этих
векторов: ![]() =36-36-0=0.
=36-36-0=0.
Отсюда
следует, что
![]() .
Т.е. диагонали четырехугольника ABCD
взаимно перпендикулярны.
.
Т.е. диагонали четырехугольника ABCD
взаимно перпендикулярны.
Некоторые приложения скалярного произведения
Угол между векторами
Определение
косинуса угла
![]() между двумя ненулевыми векторами:
между двумя ненулевыми векторами:
Отсюда следует условие перпендикулярности двух ненулевых векторов:
![]()
Проекция вектора на заданное направление
Нахождение
проекции вектора
![]() в направлении
в направлении
![]() :
:
Векторное произведение и его свойства

Опр:Три
некомпланарных вектора
![]() ,
взятые в указанном порядке, образуют
правую тройку , если из конца третьего
вектора
,
взятые в указанном порядке, образуют
правую тройку , если из конца третьего
вектора
![]() кратчайший поворот от первого вектора
кратчайший поворот от первого вектора
![]() ко второму вектору
ко второму вектору
![]() виден совершающимся против часовой
стрелки, если же поворот виден по часовой
стрелке, то тройка векторов является
левой.
виден совершающимся против часовой
стрелки, если же поворот виден по часовой
стрелке, то тройка векторов является
левой.
Опр:
Векторным
произведением
вектора
![]() на вектор
на вектор
![]() называется
такой вектор
называется
такой вектор
![]() ,
который:
,
который:
-
перпендикулярен векторам
 и
и
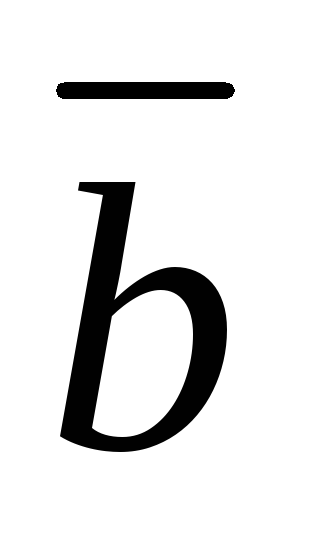 ;
; -
имеет длину, численно равную площади параллелограмма, построенного на векторах
 и
и
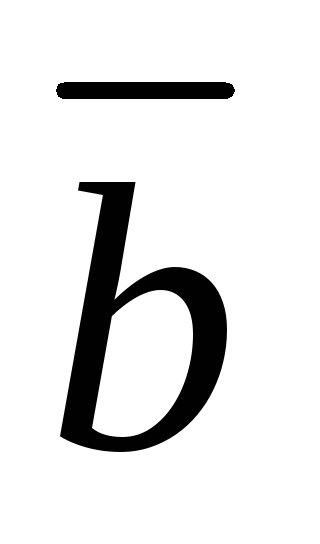 как на сторонах, т.е.
как на сторонах, т.е.
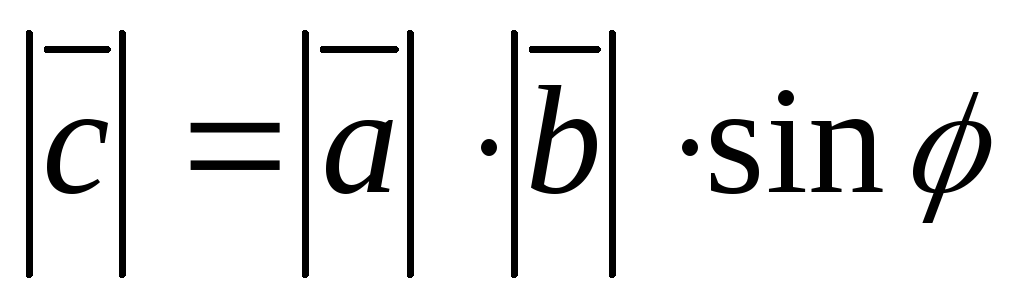 ,
где
,
где
 угол между
угол между
 и
и
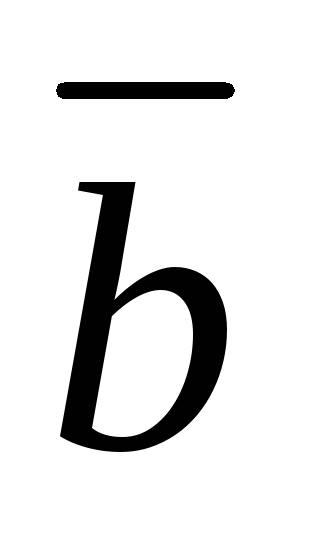
-
векторы
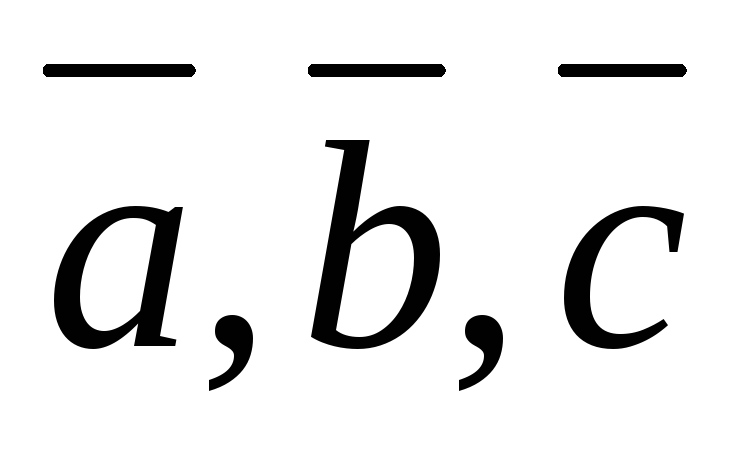 образуют правую тройку.
образуют правую тройку.
Векторное
произведение обозначается
![]() или
или
![]() .
Из определения
векторного произведения непосредственно
вытекают следующие соотношения между
ортами:
.
Из определения
векторного произведения непосредственно
вытекают следующие соотношения между
ортами: