Решение однородных систем

Система линейных уравнений называется однородной, если правые части уравнений равны нулю:

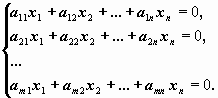
Матричный вид однородной системы: Ax=0.

Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:

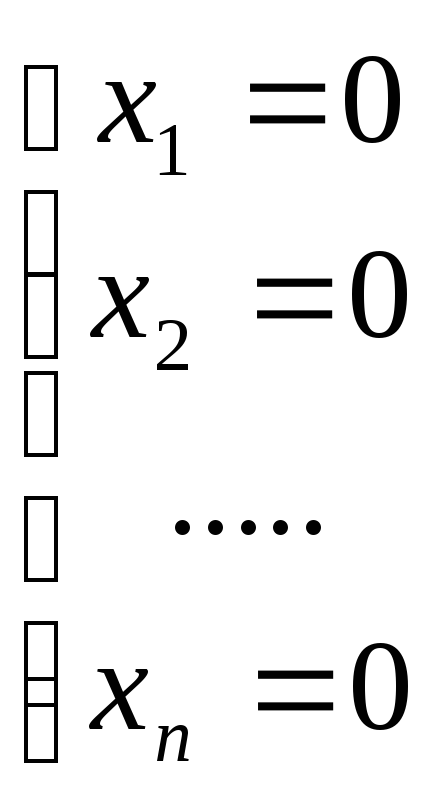
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю. Линейная комбинация решений однородной системы также является решением этой системы.

Пример: Исследовать однородную систему на совместность, найти решения: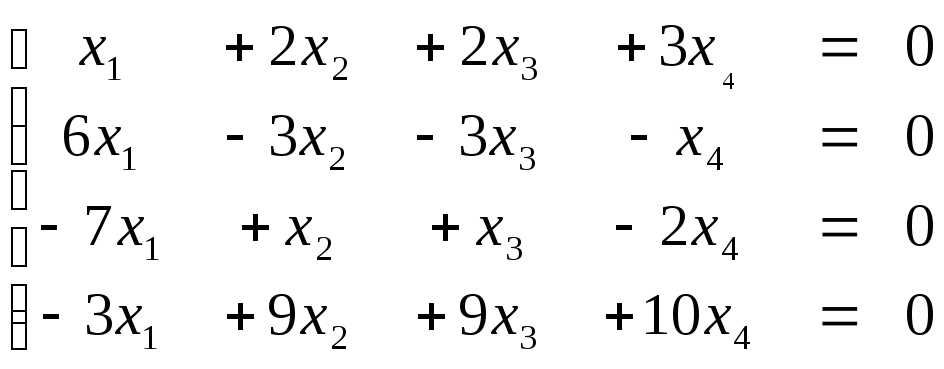

Решение: Расширенную матрицу системы приведем к ступенчатому виду: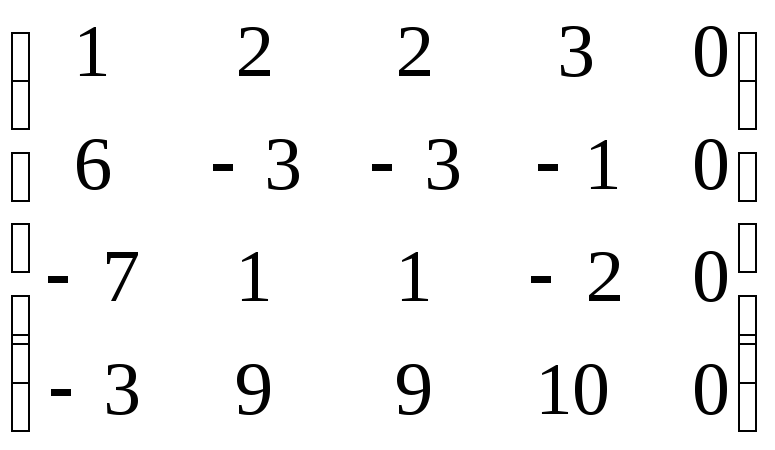

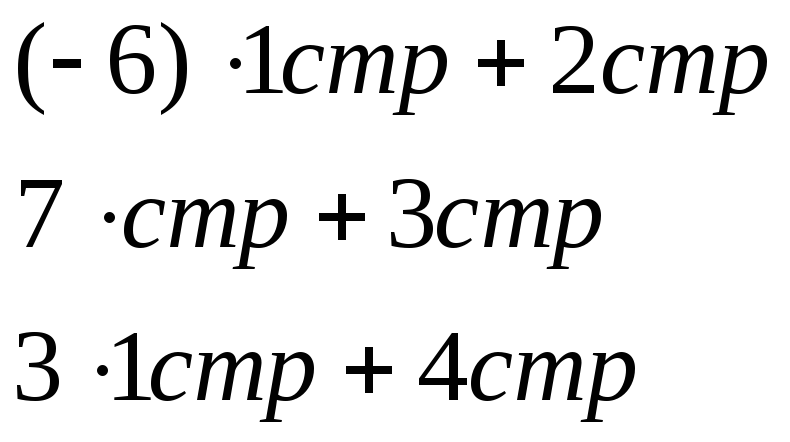
восстановим систему:

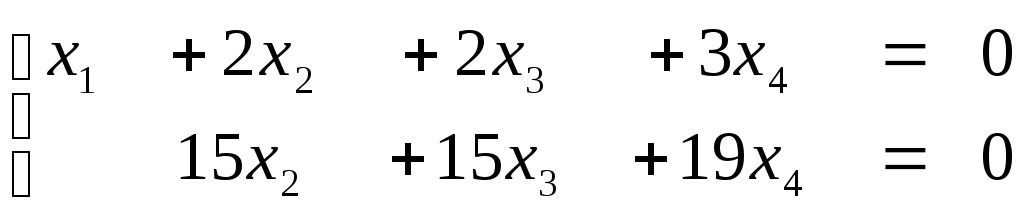
Система имеет множество решений. и главные переменные, и свободные переменные. Перенесем свободные переменные в правые части уравнений.

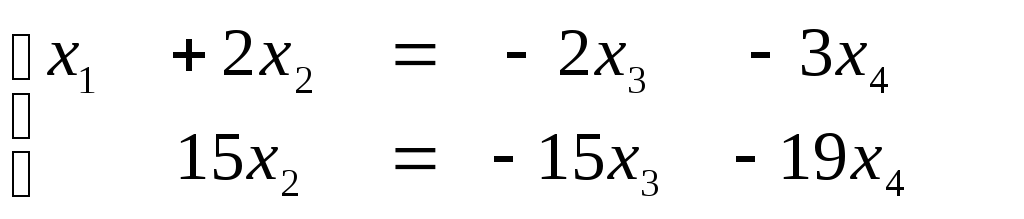
Из второго уравнения находим подставляя это выражение в первое уравнение, получим:

Общее решение системы:

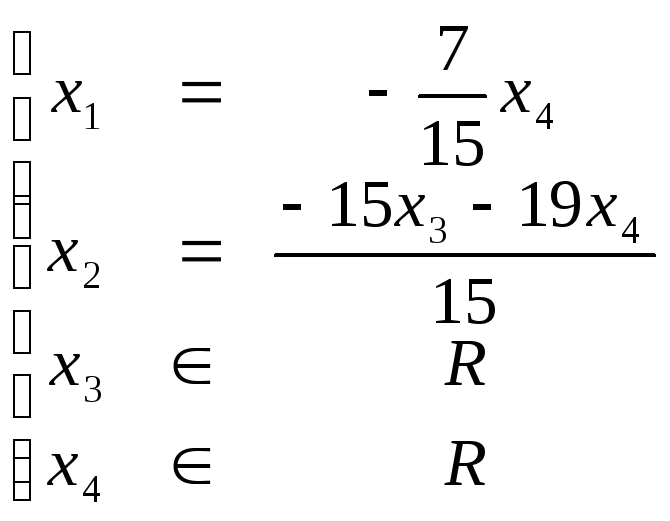
Для нахождения частных решений, свободным переменным даем произвольные значения:

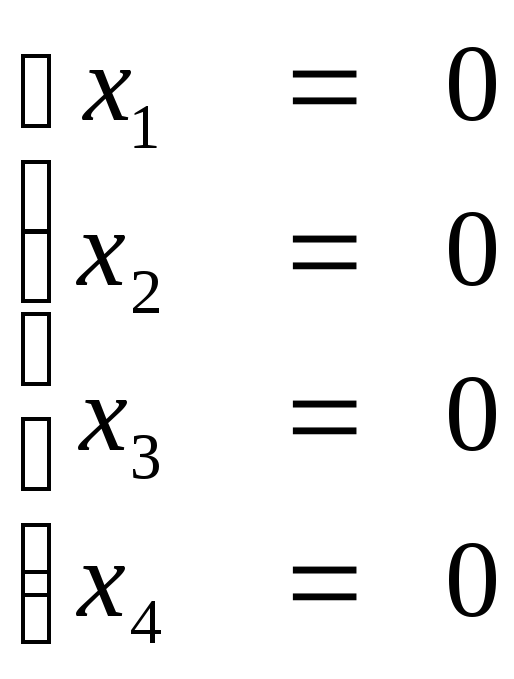
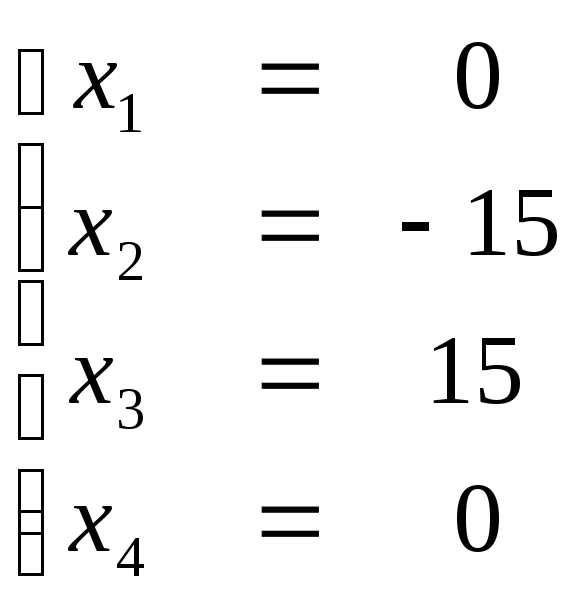
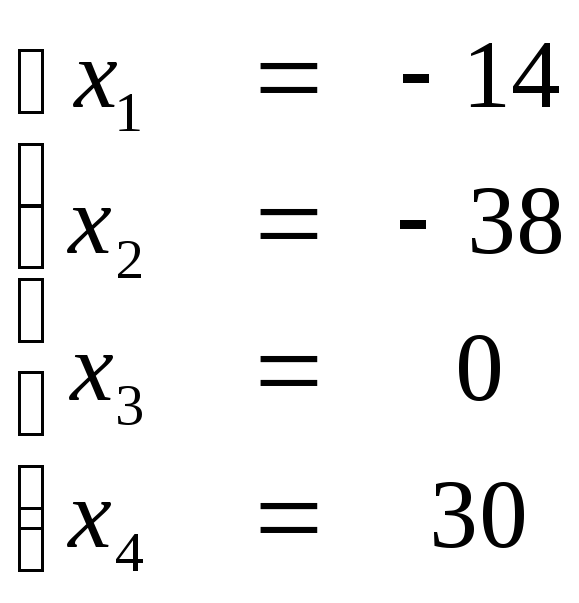
Элементы векторной алгебры Векторы

Величины, которые полностью определяются своим численным значением, называются скалярными. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными.

Вектор-это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А- начало вектора, а В- его конец, то вектор обозначается символом , или . Вектор ( у него начало в точке В , а конец в точке А) называется противоположным вектору. Вектор, противоположный вектору , обозначается .

Длиной или модулем вектора называется длина отрезка AB и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .

Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы ║

Коллинеарные векторы могут быть направлены одинаково, т.е. быть сонаправленными (), или быть противоположно направленными ().

Нулевой вектор считается коллинеарным любому вектору.

Два вектора и называются равными (), если они коллинеарные, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора перемешать в любую точку пространства.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или хотя бы два коллинеарные, то такие векторы будут компланарны.