Проекция точки на прямую

Пусть необходимо спроектировать точку на прямую Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор . Составим уравнение проецирующей прямой. Она проходит через точку и параллельна вектору . Подставив координаты точки и вектора в каноническое уравнение прямой , получим:. Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему: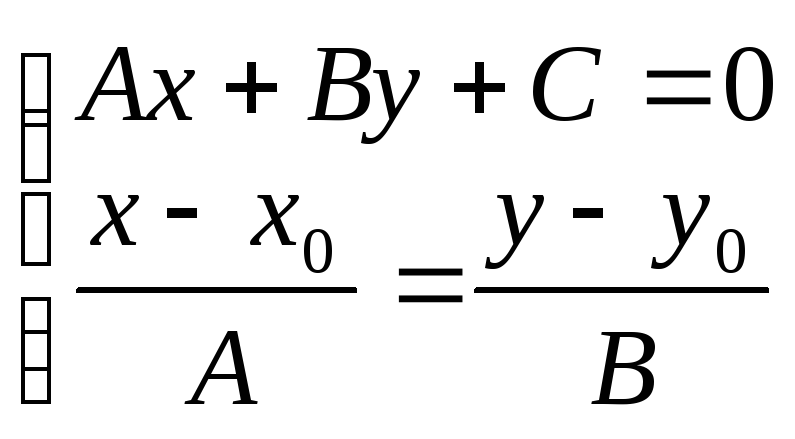решение этой системы есть координаты точки, являющейся проекцией точки на прямую

Пример: Даны вершины треугольника : ; ;. Найти:

1) уравнение высоты, опущенной из вершины ;

2) точку пересечения высоты и стороны ;

3) точку пересечения медиан треугольника .

Решение: 1) Составим уравнение высоты , проходящей через точку перпендикулярно вектору :

; , .

Ответ: .

2) Составим уравнение стороны :

, , ,

.

Найдем точку пересечения высоты и стороны .Обозначим эту точку N, она является проекцией точки А на сторону ВС. Для нахождения точки N, решим следующую систему уравнений:

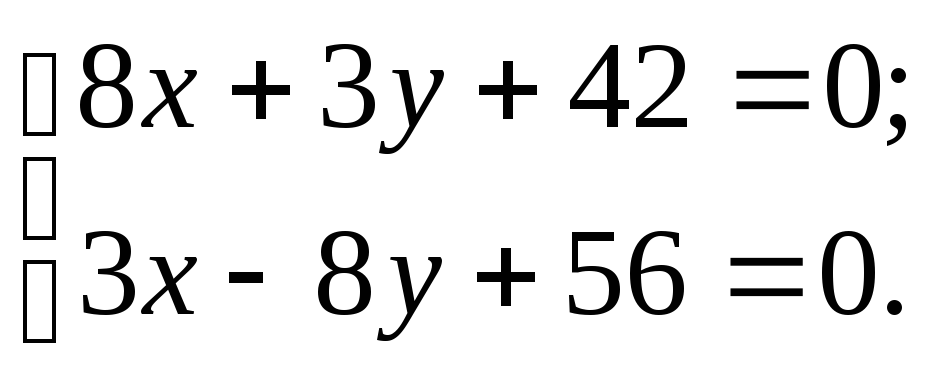
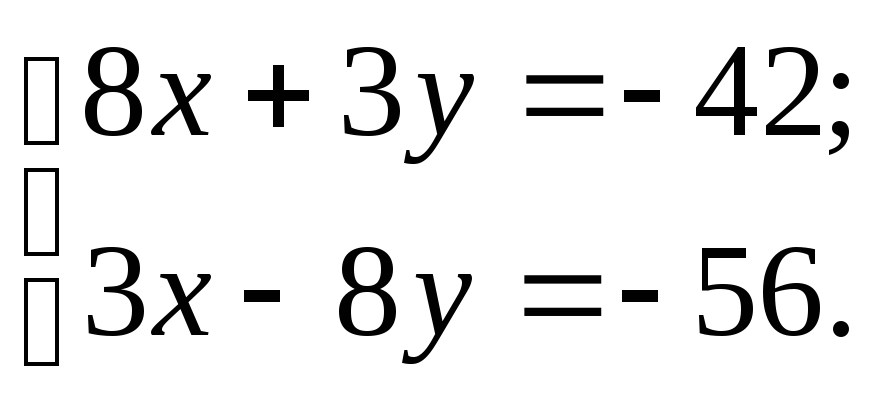
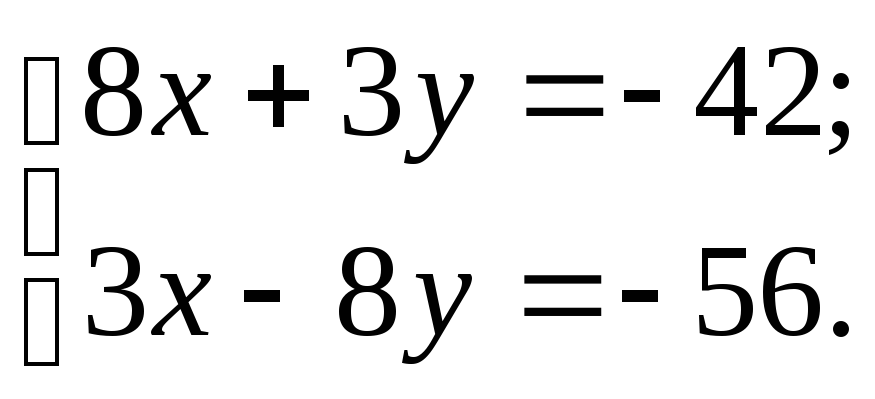
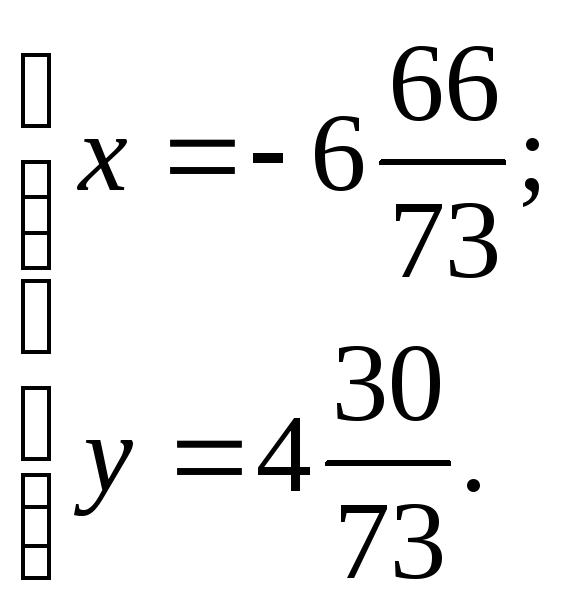
Ответ: N.

3) Найдем середину стороны :

, , , .

Составим уравнение прямой проходящей через точку и точку М:

, , ,

.

Найдем середину стороны :

, .

, .

Составим уравнение прямой проходящей через точку и точку N:

, , ,

.

Найдем точку О пересечения найденных медиан:

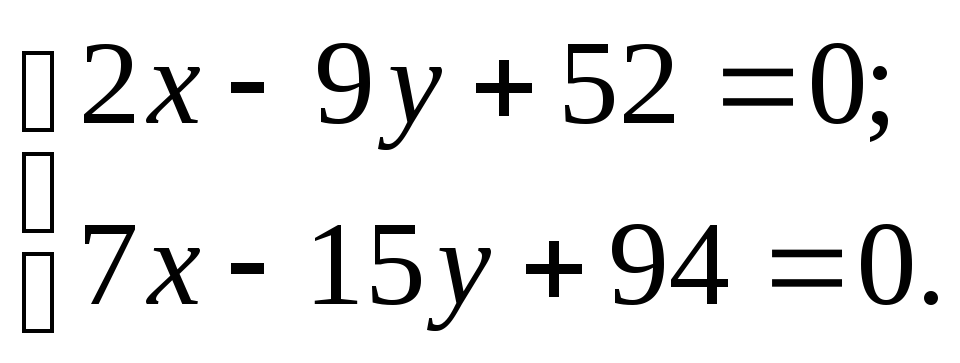
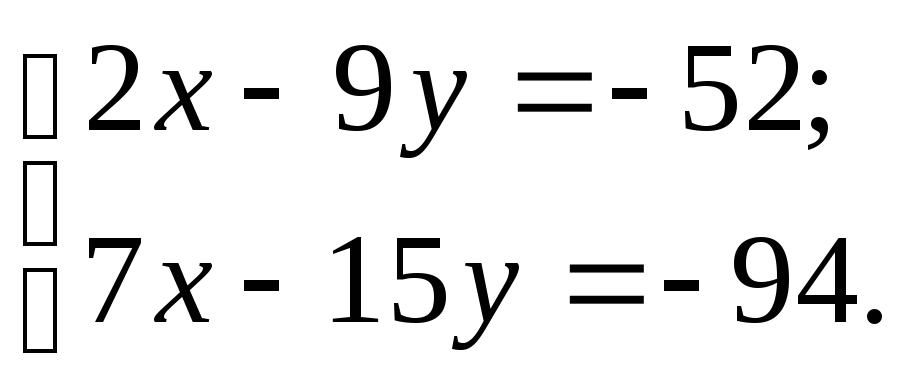
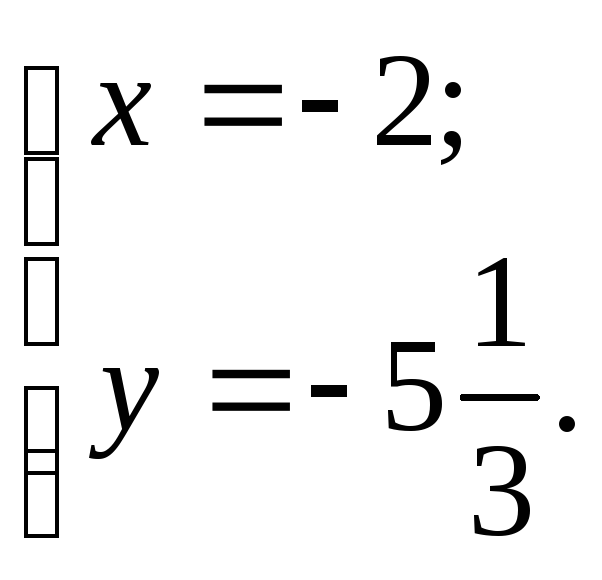
Ответ: О.

Плоскость Общее уравнение плоскости

Алгебраическое уравнение первой степени в пространстве определяет плоскость. Общее уравнение плоскости можно записать в виде:

Ax+ By+ Cz+ D=0

Любую плоскость можно представить в виде такого уравнение единственным способом. с точностью до коэффициента (т. е. при умножении уравнения на число, полученное уравнение задает ту же плоскость ) Плоскость в пространстве можно задать различными способами, рассмотрим некоторые из них:

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Опр.: Нормалью к плоскости называется вектор, перпендикулярный к данной плоскости.

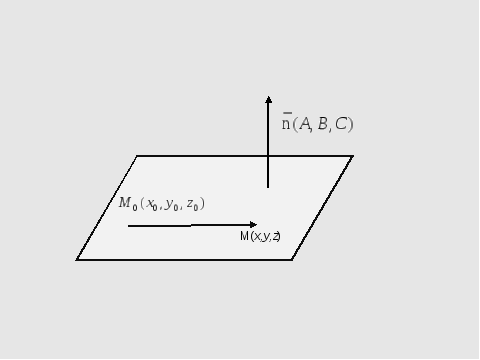
Пусть необходимо составить уравнение плоскости, проходящей через заданную точку и перпендикулярной вектору .

Предположим, что такая плоскость построена, возьмем на ней произвольную точку М(x,y,z) . Составим вектор . Вектор перпендикулярен вектору , следовательно, их скалярное произведение равно нулю: , это условие имеет вид::

Данный способ задания плоскости называется плоскость по точке М( и нормали . Имея уравнение плоскости в общем виде: Ax+ By+ Cz+ D=0, можно выписать нормаль к плоскости .

Пример: Составить уравнение плоскости, проходящей через точку А(1,2,-3), параллельно плоскости 3x-4y+5z-2=0

Решение: Выпишем нормаль к плоскости, т.е. вектор перпендикулярный плоскости: . Так как необходимо построить плоскость параллельную данной, то можно использовать вектор в качестве нормали к искомой плоскости. Составляем уравнение плоскости по точке А и нормали : после преобразования получим: 3x-4y+5z+20=0

Ответ: 3x-4y+5z+20=0.