
- •Определители
- •Свойства определителя:
- •Обратная матрица
- •Правило вычисления обратной матрицы:
- •Решение систем линейных алгебраических уравнений
- •Решение однородных систем
- •Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Сумма векторов
- •Разность векторов
- •Умножение вектора на число
- •Проекция вектора на ось
- •Свойства проекций:
- •Линейные операции над векторами, заданными в координатной форме:
- •Представление вектора в декартовой системе координат
- •Направляющие косинусы вектора
- •Координаты точки, радиус-вектор точки
- •Деление отрезка в данном отношении
- •Произведения векторов Скалярное произведение векторов и его свойства
- •Свойства скалярного произведения
- •Выражение скалярного произведения через координаты сомножителей
- •Некоторые приложения скалярного произведения
- •Векторное произведение и его свойства
- •Свойства векторного произведения
- •Выражение векторного произведения через координаты сомножителей
- •Приложения векторного произведения
- •Смешанное произведение векторов
- •Свойства смешанного произведения
- •Выражение смешанного произведения через координаты сомножителей
- •Приложения смешанного произведения
- •Прямая на плоскости Линия на плоскости
- •Общее уравнение прямой линии на плоскости
- •Прямая, проходящая через точку, перпендикулярно данному вектору
- •Прямая, проходящая через точку, параллельно данному вектору
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой в отрезках
- •Уравнение прямой с угловым коэффициентом
- •Прямая, проходящая через точку, в данном направлении
- •Угол между прямыми
- •Точка пересечения прямых
- •Расстояние от точки до прямой
- •Проекция точки на прямую
- •Плоскость Общее уравнение плоскости
- •Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •Особенности в расположении плоскостей
- •Уравнение плоскости, проходящей через данную точку, параллельно двум неколлинеарным векторам
- •Уравнение плоскости, проходящей через три заданные точки
- •Уравнение плоскости в отрезках
- •Основные задачи
- •Прямая линия в пространстве Общее уравнение прямой
- •Уравнение прямой, проходящей через заданную точку, перпендикулярно данной плоскости
- •Перевод уравнения прямой из канонического вида в параметрический
- •Перевод уравнения прямой из общего вида в канонический
- •Угол между прямыми в пространстве
- •Взаимное расположение прямых в пространстве
- •Угол между прямой и плоскостью
- •Пересечение прямой и плоскости
- •Кривые второго порядка
- •Гипербола
- •Парабола
-
Матрицы, операции над матрицами
|
Определители
Вычисление определителей второго и третьего порядка
Квадратной
матрице А![]() порядка
n можно поставить в соответствие число,
обозначаемое det
А (или
порядка
n можно поставить в соответствие число,
обозначаемое det
А (или
![]() или
или
![]() ),
называемое ее определителем
(детерминантом),
и вычисляемое по следующим схемам:
),
называемое ее определителем
(детерминантом),
и вычисляемое по следующим схемам:
-
d
 et
А
et
А =
=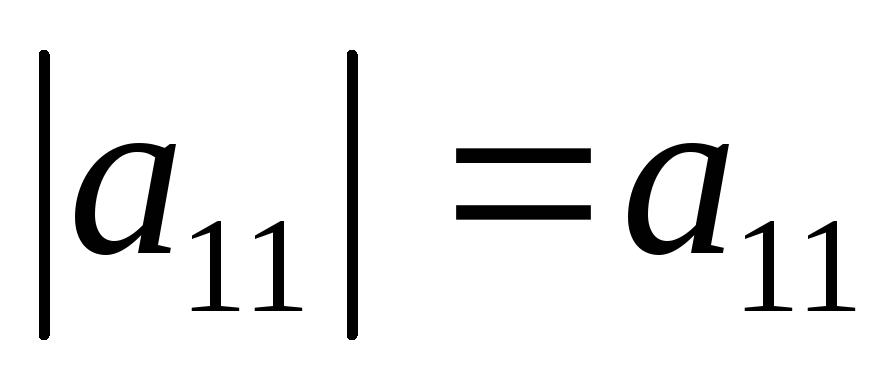
-
det А
 =
=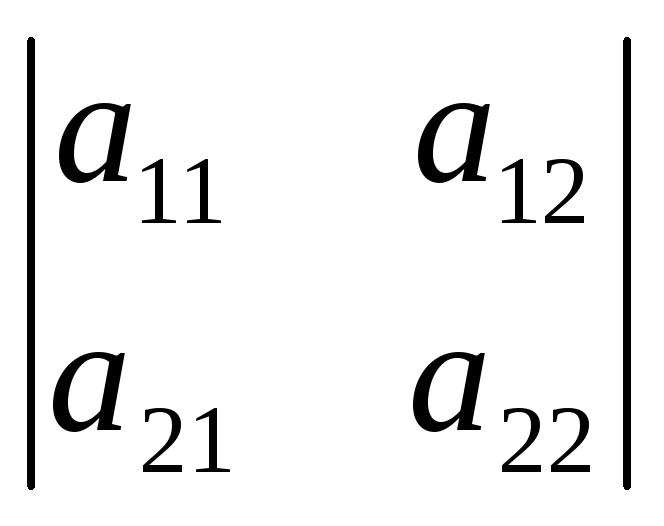 =
+=
=
+=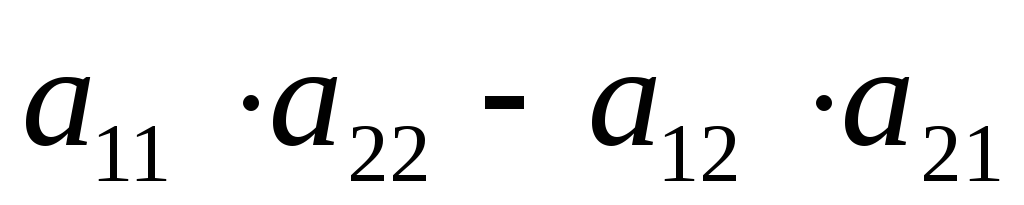
-
detА
 =
=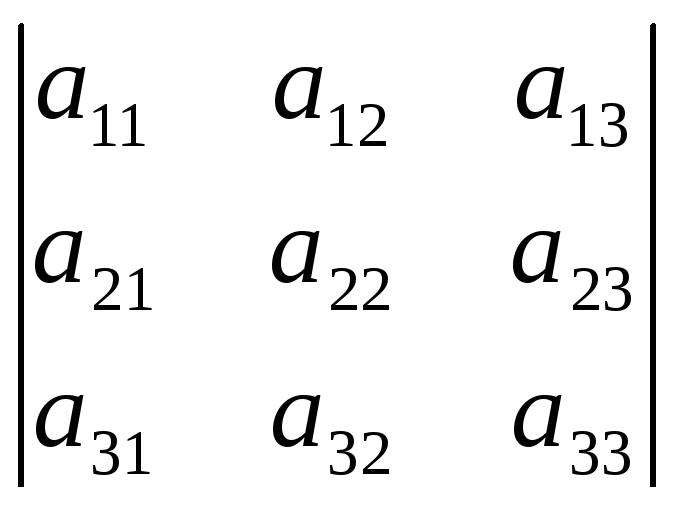 =
=
 = =
= =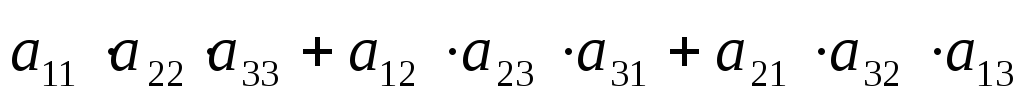 -
-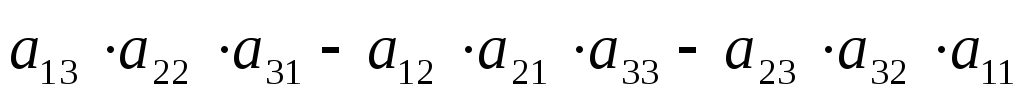
Пример:
Вычислить определители матриц А=![]() , В=
, В=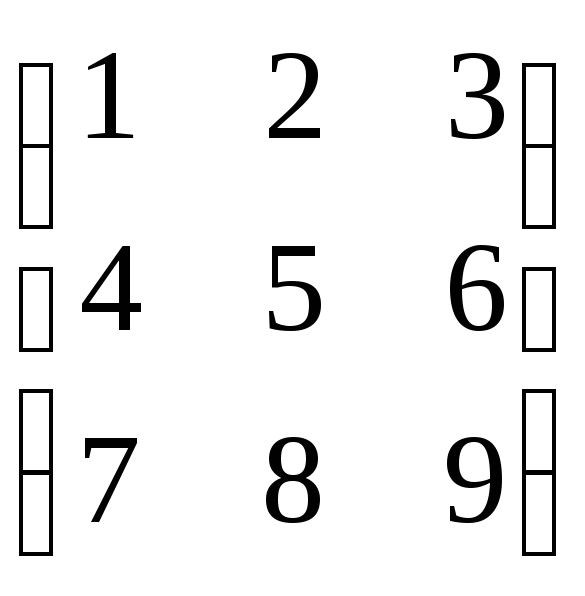
Решение:
Det
А=![]()
Det
В=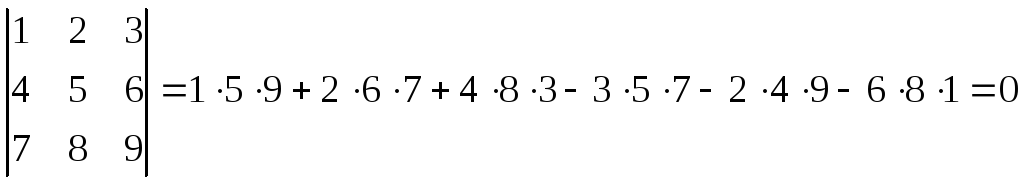
Ответ: detA=14, detB=0.
Разложение определителя матрицы по элементам строки или столбца
Опр:
Минором
![]() элемента
элемента
![]() определителя
n-го
порядка называется определитель (n-1)-го
порядка ,полученный из исходного путем
вычеркивания строки и столбца, на
пересечении которых находится элемент
определителя
n-го
порядка называется определитель (n-1)-го
порядка ,полученный из исходного путем
вычеркивания строки и столбца, на
пересечении которых находится элемент
![]() .
.
Опр:
Алгебраическим
дополнением
![]() элемента
элемента
![]() называется
его минор, умноженный на число (-1)
называется
его минор, умноженный на число (-1)![]() :
:
![]()
Теорема: Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.
Разложение определителя по любой (i-й, где i=1,2,…n) строке:
det![]()
Разложение определителя по любому (j-му, где j=1,2,…n) столбцу:
detA![]()
![]()
Пример:
Найти минор
![]() и алгебраическое дополнение
и алгебраическое дополнение
![]() элемента
элемента
![]() матрицы А=
матрицы А=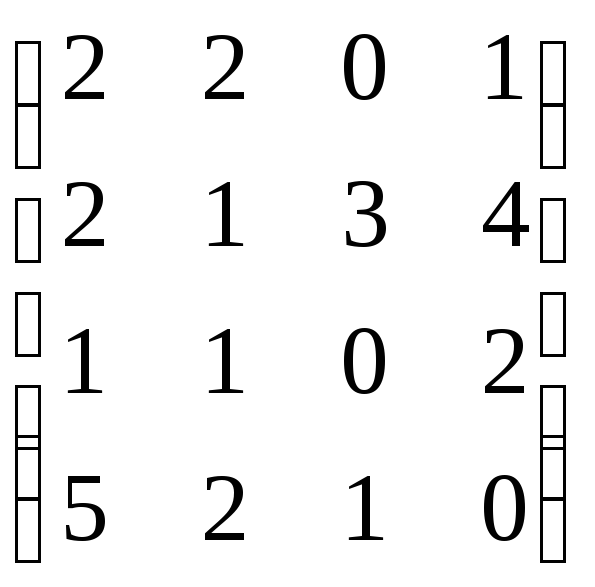 .
.
Решение:
Найдем
минор: М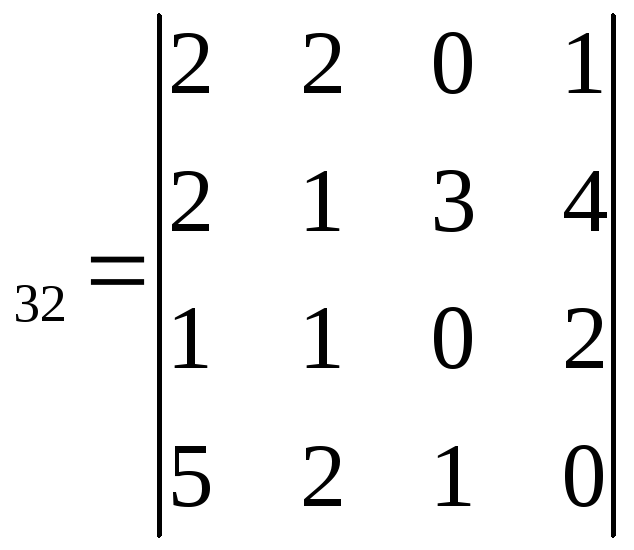 =
= =0+0+2-15-8-0=-21;
=0+0+2-15-8-0=-21;
Найдем
алгебраическое дополнение:
![]()
Ответ:
![]() ,
,
![]()
Пример:
Вычислить определитель матрицы А=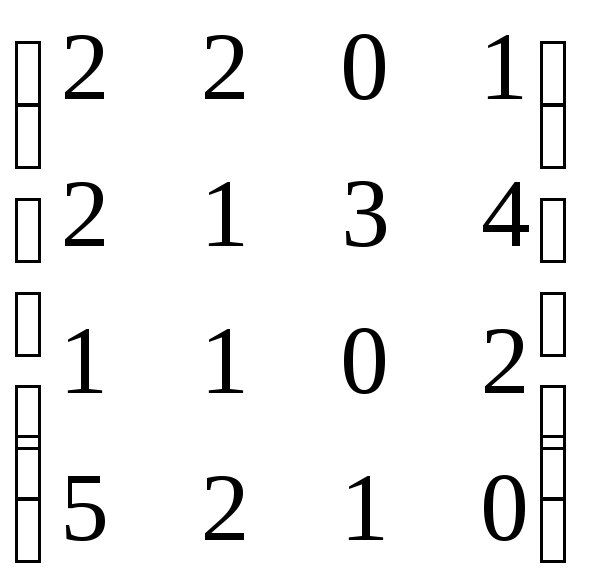 .
.
Решение: Вычислим определитель разложением по третьему столбцу:
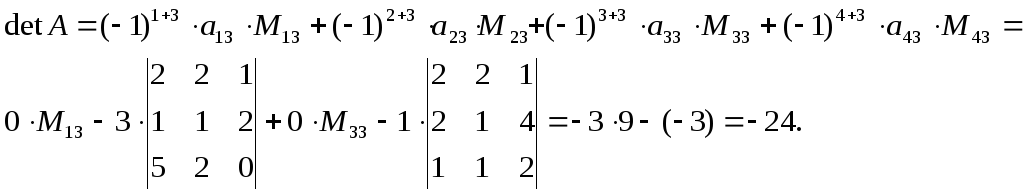
Ответ: detA=-24
Свойства определителя:
-
Определитель матрицы равен определителю транспонированной матрицы. det A=detA
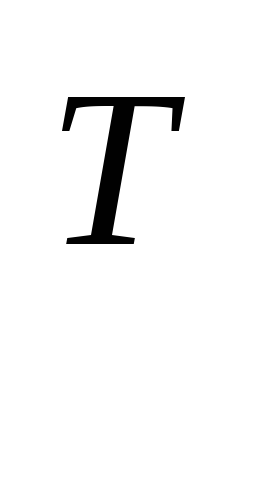 .
. -
При перестановке местами двух параллельных строк или столбцов определитель меняет свой знак на противоположный.
-
Определитель, имеющий две одинаковые , или две пропорциональные строки или столбца равен нулю.
-
Общий множитель всех элементов строки или столбца можно выносить за знак определителя, т.е.
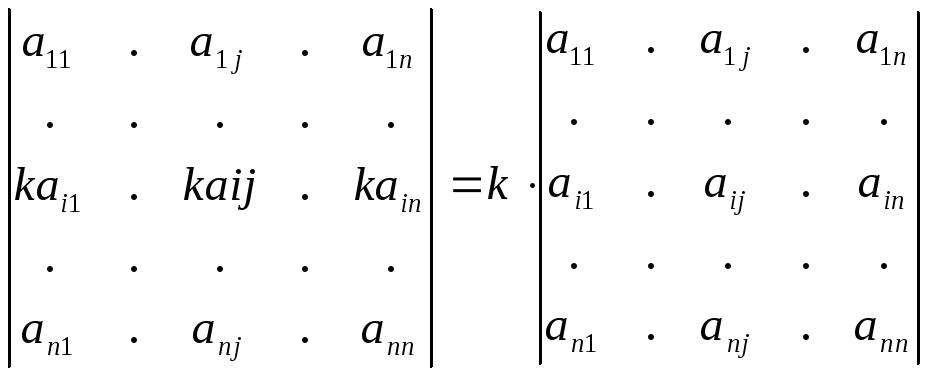
-
Определитель, имеющий нулевую строку или столбец равен нулю.
-
Определитель не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на любое число. Это утверждение верно и для столбцов.
Обратная матрица
Опр:
Квадратная матрица А называется
невырожденной,
если ее определитель не равен нулю, т.е.
det
A![]()
Опр:
Матрицей, обратной
к матрице А называется такая матрица
![]() ,
которая удовлетворяет условиям:
,
которая удовлетворяет условиям:![]() .
.
Все
матрицы: А,
![]() и Е имеют один и тот же порядок.
и Е имеют один и тот же порядок.
Всякая
невырожденная матрица имеет обратную,
которая может быть найдена по формуле:
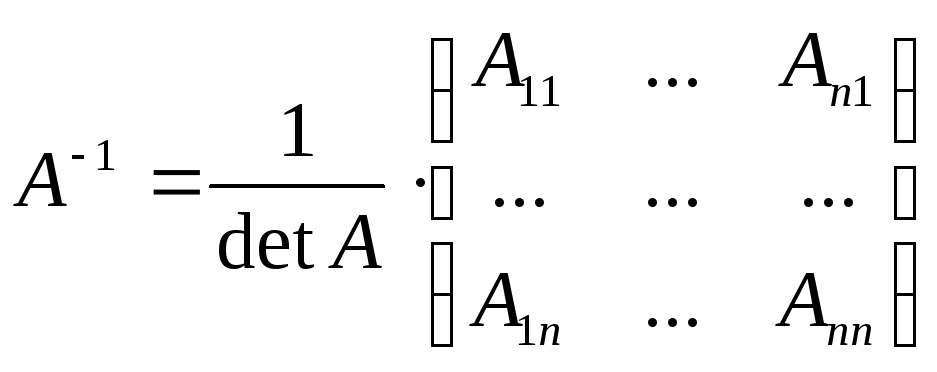 ,
где
,
где
![]() алгебраическое
дополнение элемента
алгебраическое
дополнение элемента
![]() .
Распишем последовательность нахождения
обратной матрицы:
.
Распишем последовательность нахождения
обратной матрицы:
Правило вычисления обратной матрицы:
-
Вычислить определитель матрицы detA ( detA
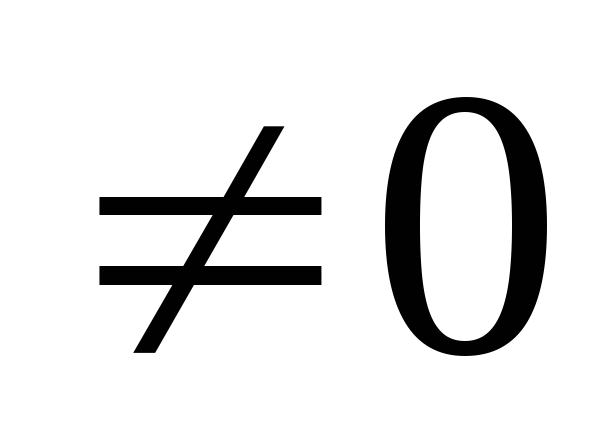 ,в
противном случае обратная не существует.)
,в
противном случае обратная не существует.) -
Составить матрицу из алгебраических дополнений элементов:
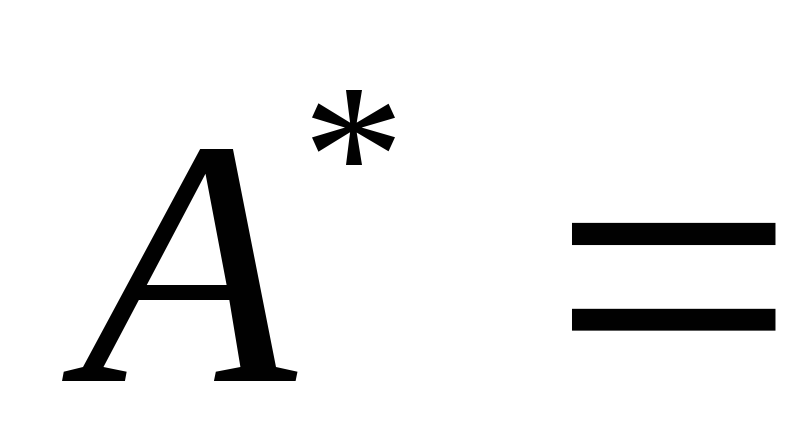
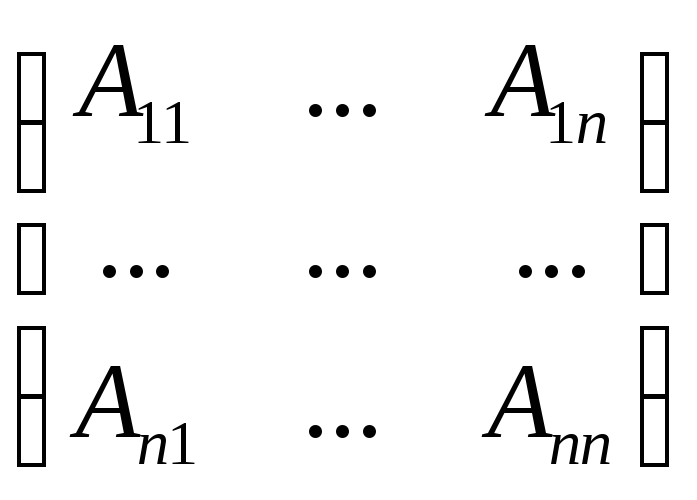
-
Каждый элемент полученной матрицы разделить на определитель:
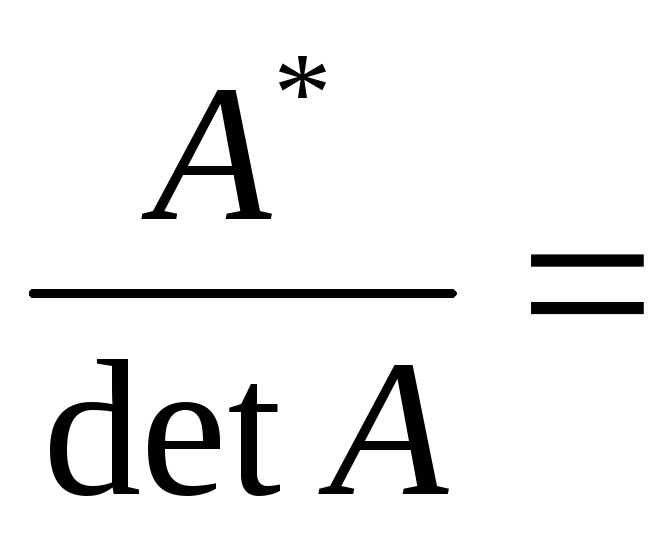
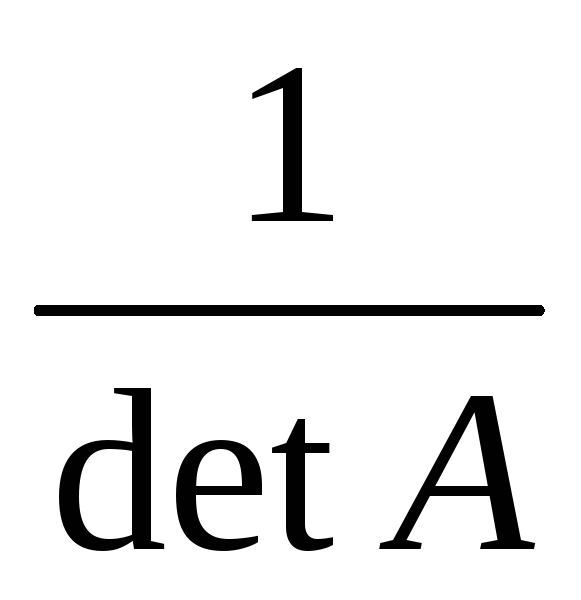
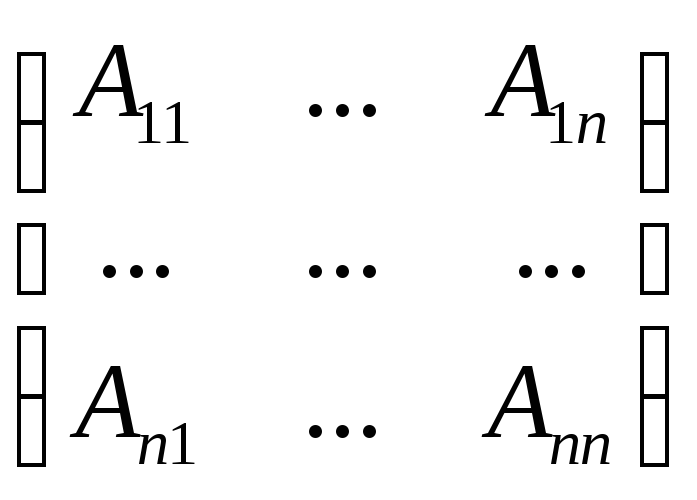
-
Транспонировать полученную матрицу:
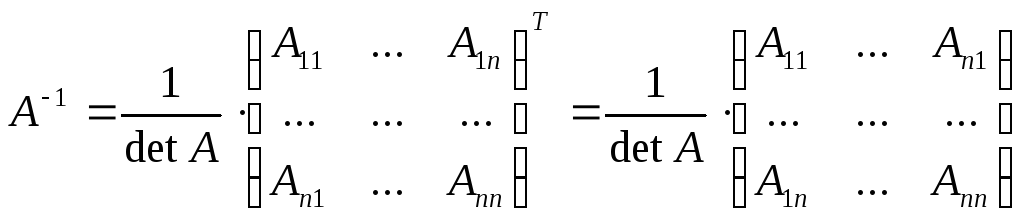
-
Результат проверить, умножив А на
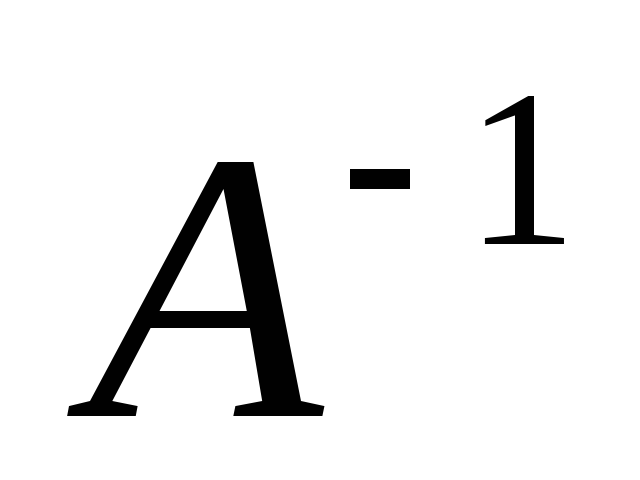 .
.
Пример:
Для матрицы А=![]() найти обратную.
найти обратную.
Решение:
-
Находим detA=

-
Составляем матрицу
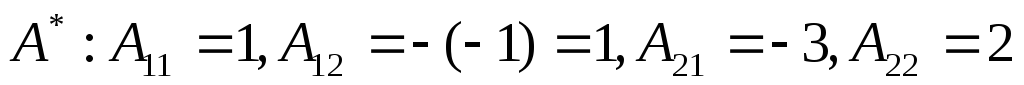 ,
поэтому
,
поэтому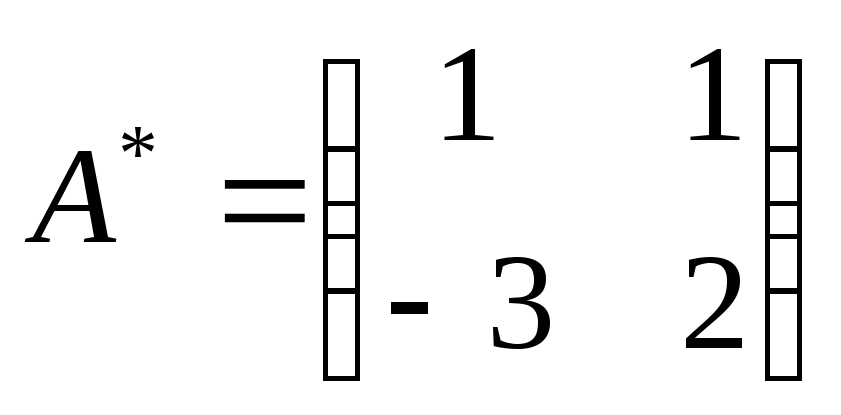
-
Делим элементы на определитель:
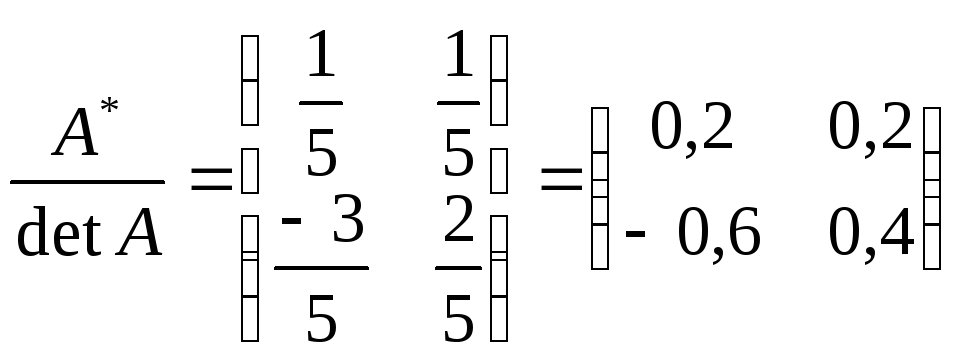
-
Транспонируем полученную матрицу:
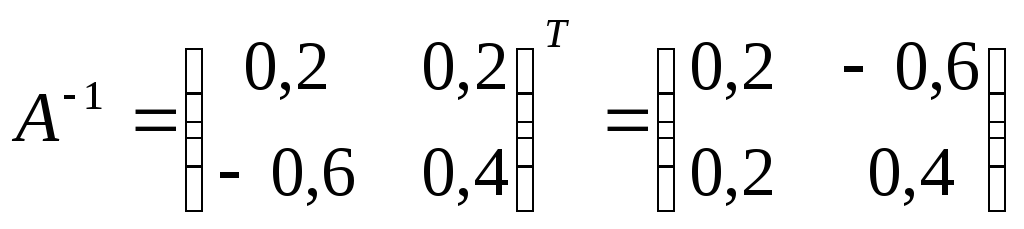
-
Проверка:
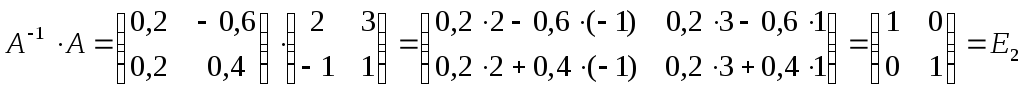
Ответ:
![]()
Пример:
Для матрицы А= найти обратную.
найти обратную.
Решение:
Находим
detA=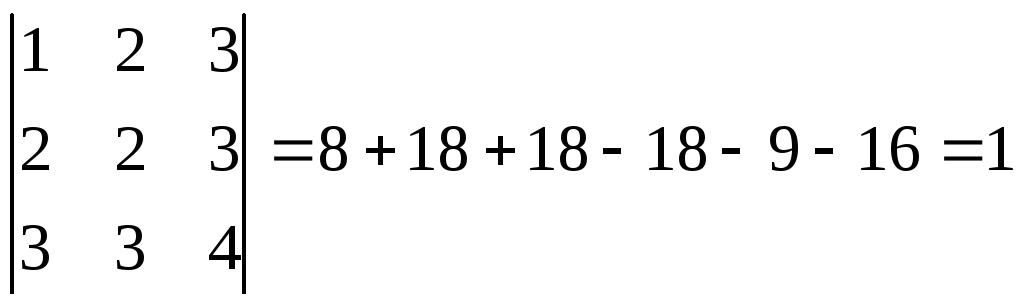
Составляем матрицу
![]()
![]()
![]() поэтому
поэтому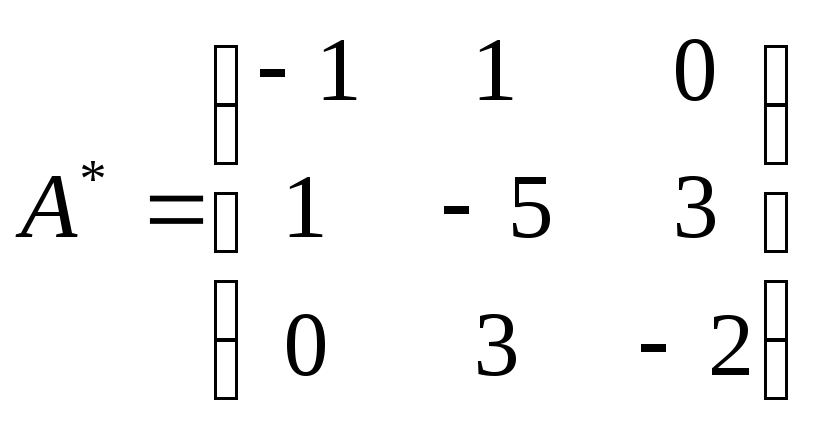
Делим
элементы на определитель: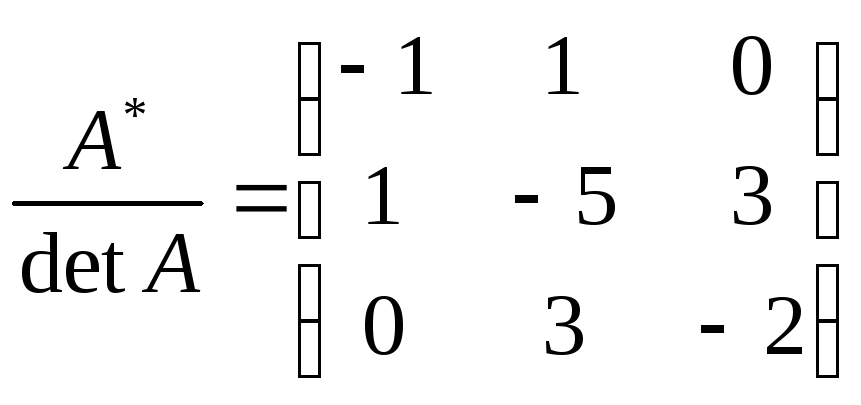
Транспонируем
полученную матрицу: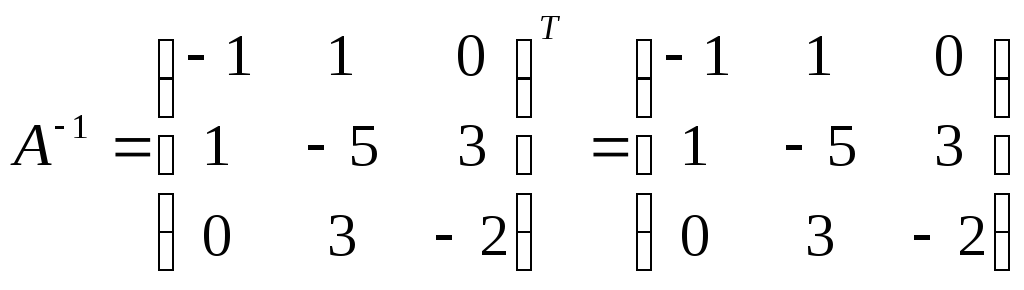
Проверка: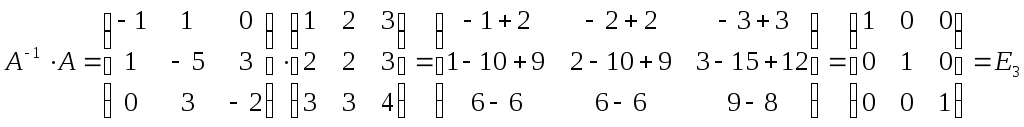
Ответ:
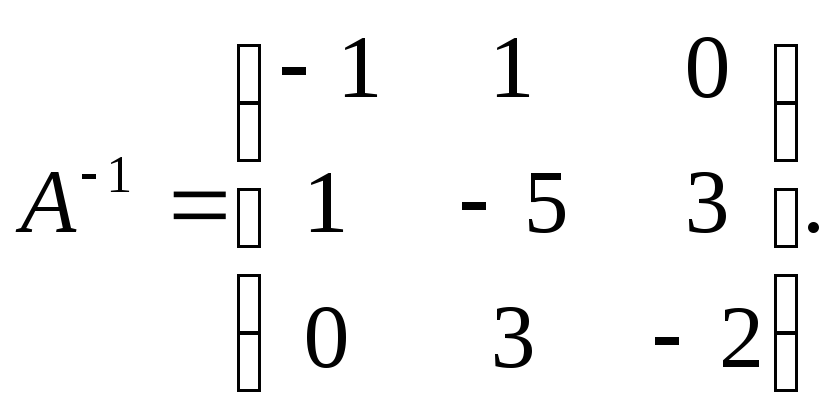

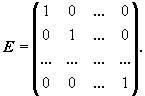
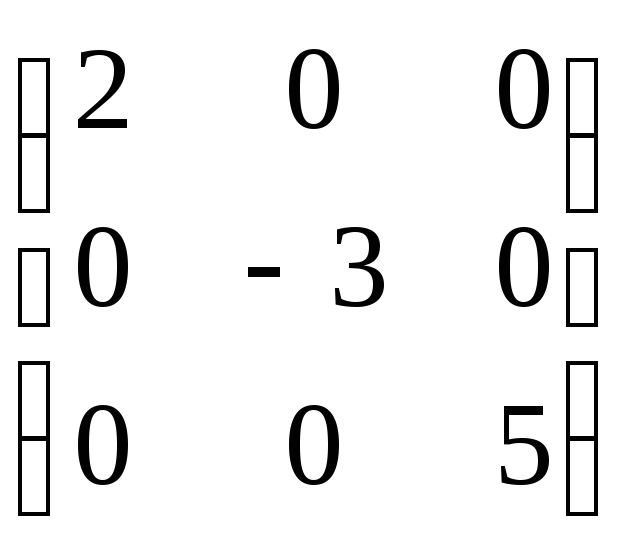 ;
B=
;
B= ;
E3=
;
E3=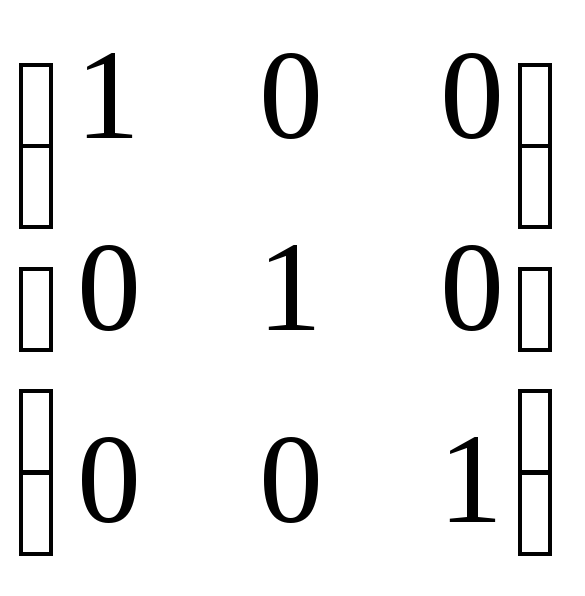 ;
O2=
;
O2=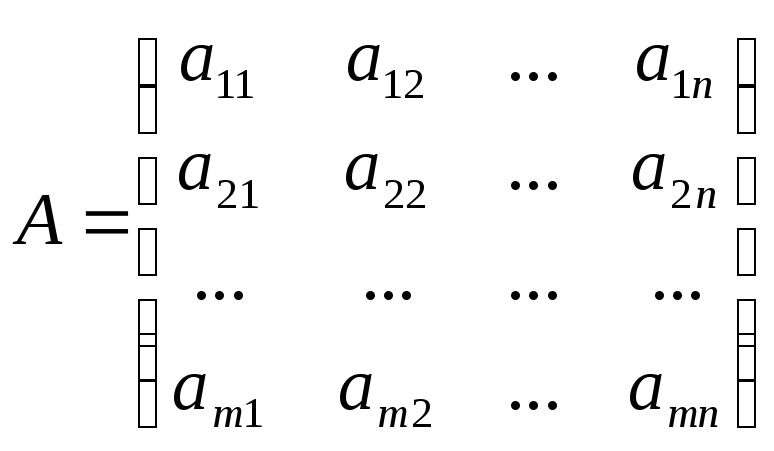 при
транспонировании получим:
при
транспонировании получим: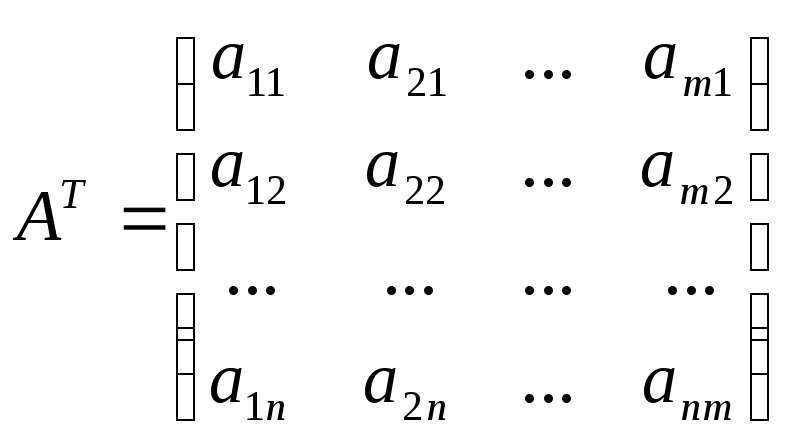
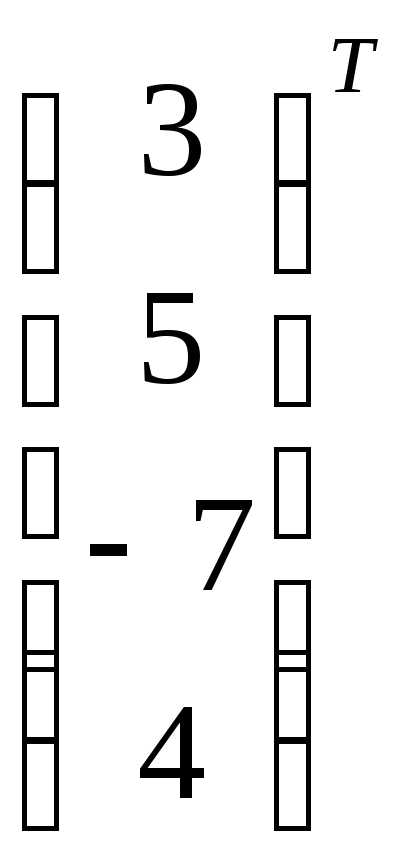 =
=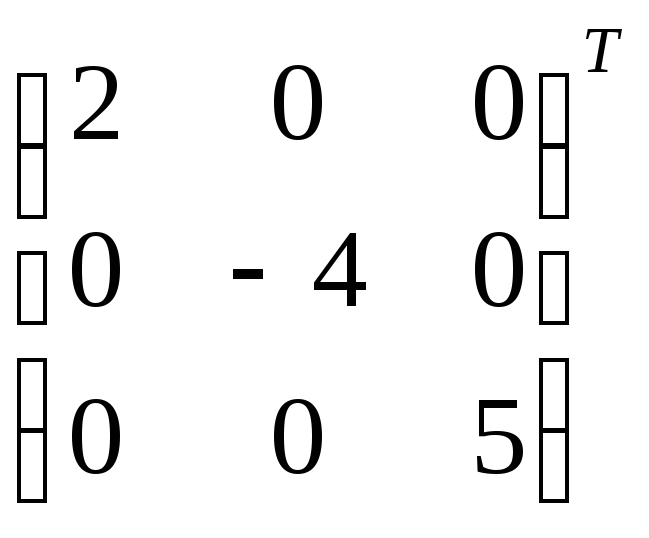 =
=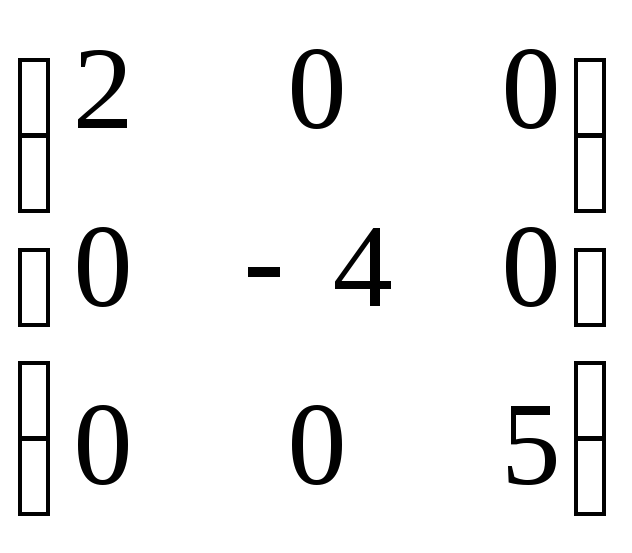 .
.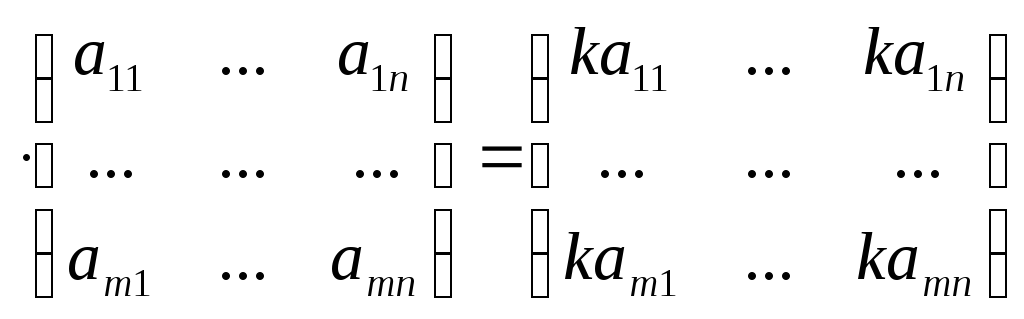
 Сложение
матриц:
Сложение
матриц: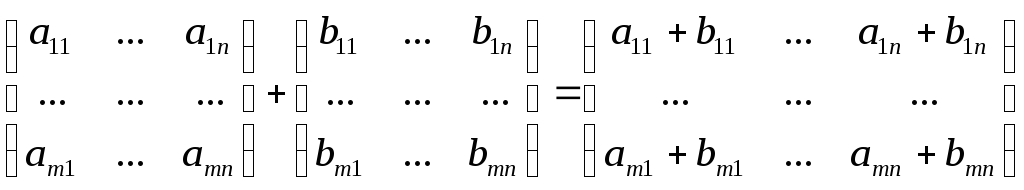
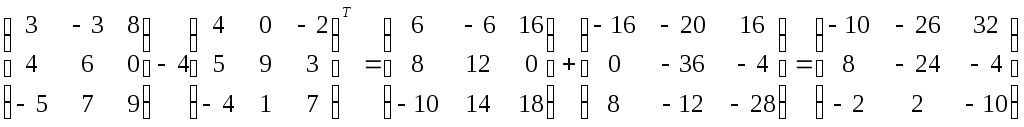
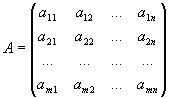 ,
,
 ,
, ,
, .
.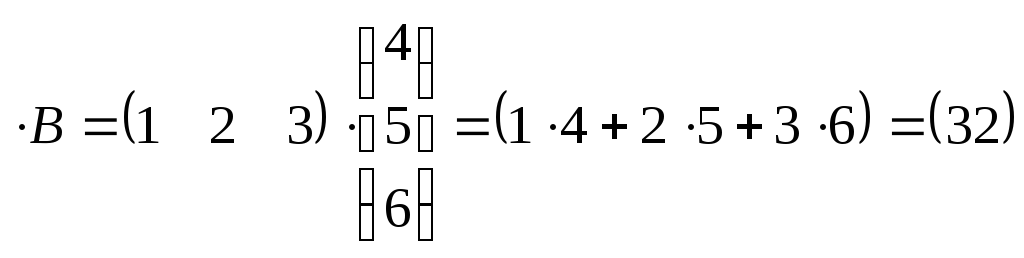
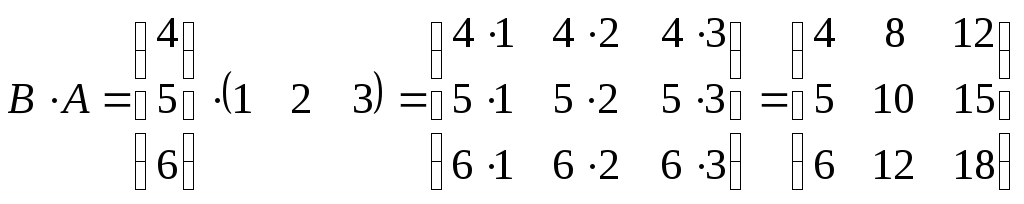
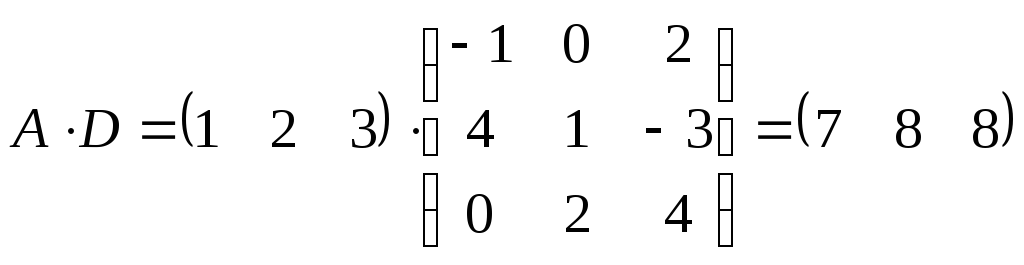 ;
D
;
D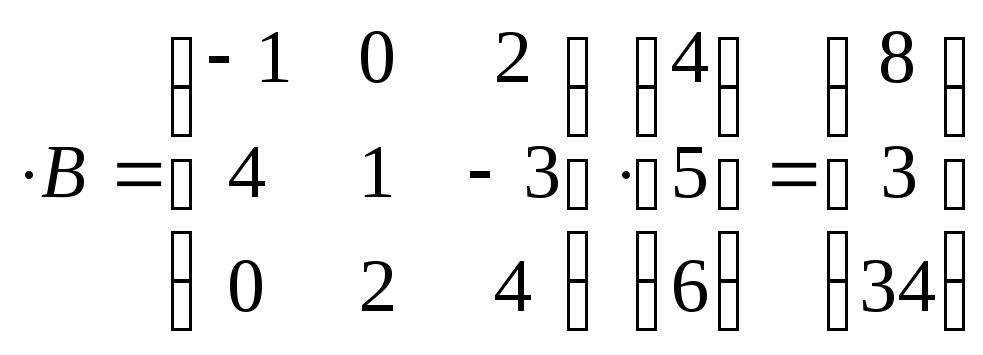 ;
B
;
B