Глава 7. Анализ и синтез сигналов с помощью преобразования Фурье.
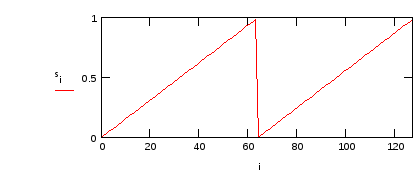
Определим функцию,
задающую так называемый пилообразный
сигнал
и изобразим ее на графике
Заполним массив
s:
Проводим прямое
преобразование Фурье: 
Внимание!
В том случае, когда в массиве s
содержится
элементов, причем все числа
действительные, следует использовать
функцию fft. Во всех остальных
случаях – функцию cfft. Массив
g содержит комплексные коэффициенты
дискретного преобразования Фурье.
Размер массива
f –
Для анализа вклада отдельных гармоник в исходный сигнал изобразим на графике модули и аргументы гармоник
Проводим обратное преобразование Фурье, исключив гармоники с малым вкладом. Будем учитывать только гармоники с амплитудой не менее 0.3. Для отсечения слагаемых с малым вкладом воспользуемся функцией единичного скачка – функцией Хевисайда Ф.
Для обратного преобразования Фурье используется функция ifft, если прямое преобразование осуществлялось с помощью fft, и cifft, если прямое преобразование осуществлялось с помощью cfft.
Повторим преобразование Фурье, учтя слагаемые с амплитудой до 0.1.
Учет дополнительных гармоник существенно улучшил результат синтеза сигналов.
8. Исходные материалы.
При выполнении данной работы были использованы материалы сайтов:
-
http://www.mathworks.com
-
www.exponenta.ru
-
http://www.matlab.ru
1 Получите эти формулы самостоятельно по аналогии с методом Ньютона, оставив в разложении Тейлора первые три слагаемых.
2
К сожалению, это не всегда так. Если
начальное приближение выбрано неудачно
и значение производной в этой точке
близко к нулю, то, вообще говоря, найденный
корень может быть не ближайшим к
начальному приближению. В качестве
примера решите самостоятельно задачу
поиска корня уравнения
,
выбрав в качестве начального приближения
число близкое к
.
Чем ближе к
будет
выбранное значение, тем более далекий
от 0 корень мы будем получать.